Содержание
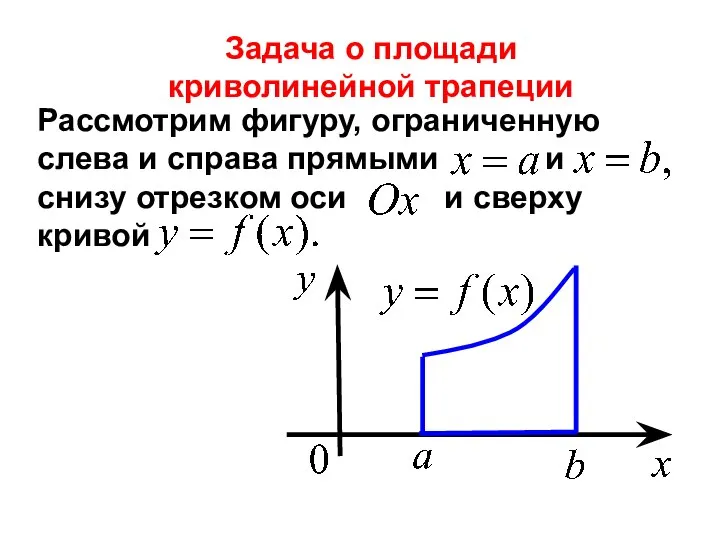
- 2. Рассмотрим фигуру, ограниченную слева и справа прямыми и снизу отрезком оси и сверху кривой Задача о
- 3. 1) Разобьем отрезок на малых отрезков с помощью точек деления Такая фигура называется криволинейной трапецией. Вычислим
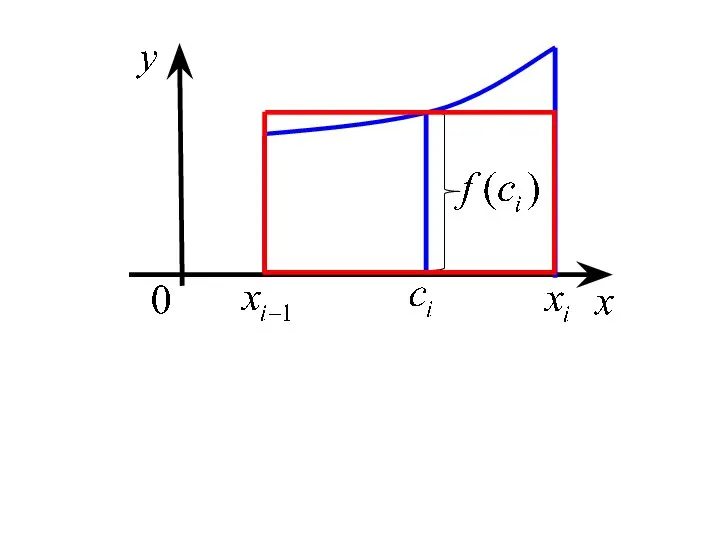
- 4. 2) В каждом из отрезков возьмем произвольную точку где 3) Составим сумму Назовем её интегральной суммой.
- 5. 4) Назовем определенным интегралом и обозначим
- 6. Произведение численно равно площади прямоугольника с основанием и высотой Числа и называют верхним и нижним пределами
- 8. Геометрический смысл определенного интеграла: (предполагается, что ).
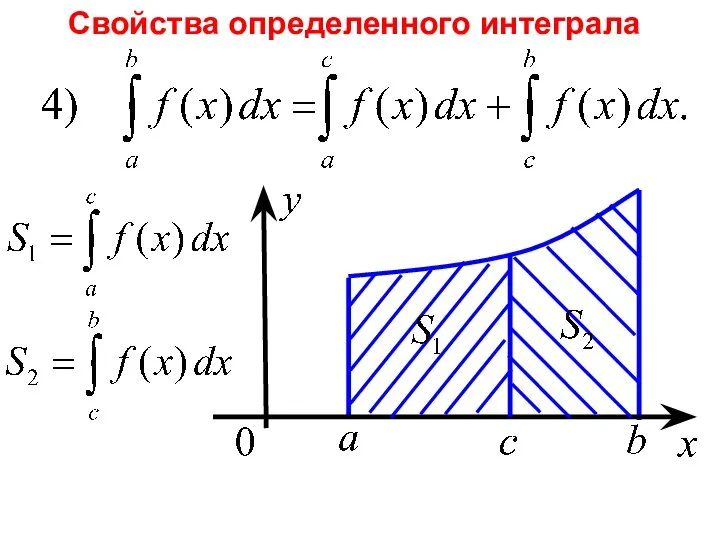
- 9. Свойства определенного интеграла
- 10. Свойства определенного интеграла
- 11. Свойства определенного интеграла
- 12. Теорема о среднем значении Если - непрерывная на функция, то существует такая точка что
- 13. Формула Ньютона-Лейбница И. Ньютон (1642-1727) – великий английский математик Г. Лейбниц (1646-1716) – великий немецкий математик.
- 14. Примеры Предполагается, что - непрерывная функция.
- 15. Замена переменной в определенном интеграле Замена: Новые пределы интегрирования:
- 17. Если то Если то
- 20. Самостоятельная работа №1
- 22. Скачать презентацию











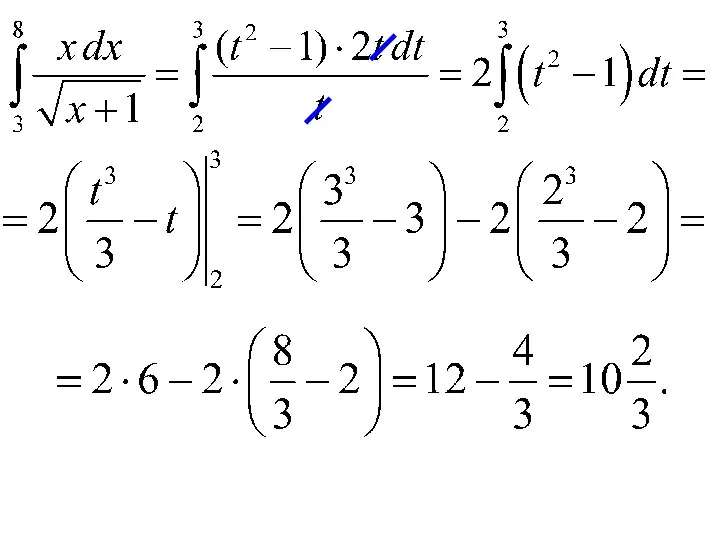
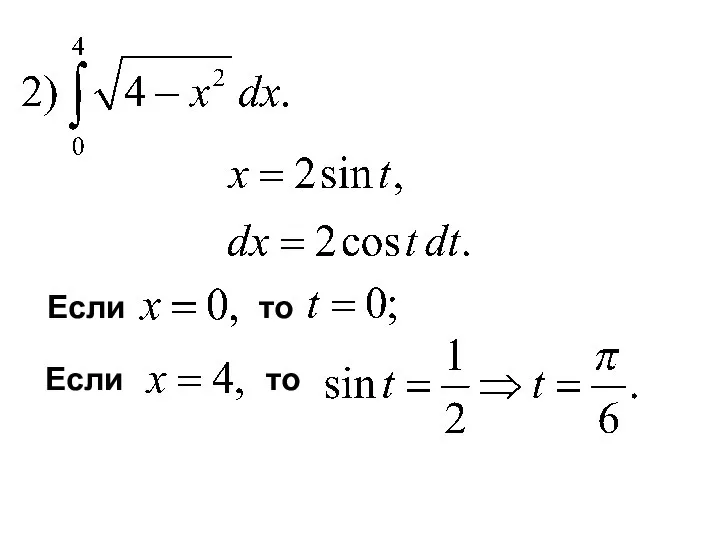
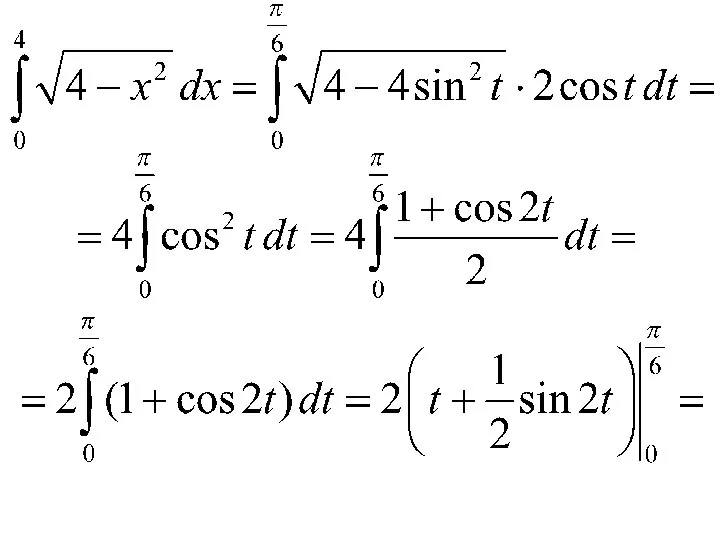
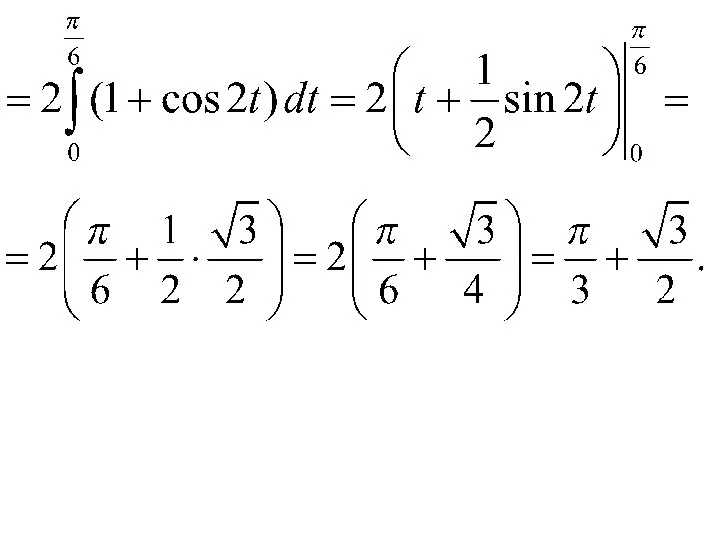

 Системи комп’ютерної математики
Системи комп’ютерної математики Дидактические игры по математике. Найди соседей числа (для дошкольников)
Дидактические игры по математике. Найди соседей числа (для дошкольников) Функции нескольких переменных. (Лекция 2)
Функции нескольких переменных. (Лекция 2) Площади фигур в свете подготовки к ГИА - 9 класс
Площади фигур в свете подготовки к ГИА - 9 класс Сложение и вычитание десятичных дробей. Урок с использованием интерактивной доски
Сложение и вычитание десятичных дробей. Урок с использованием интерактивной доски Презентация по математике "Перевод чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную" - ска
Презентация по математике "Перевод чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную" - ска Решение задач по теме «Соотношения между сторонами и углами в прямоугольном треугольнике»
Решение задач по теме «Соотношения между сторонами и углами в прямоугольном треугольнике» Основы нечеткой логики
Основы нечеткой логики Свойства тригонометрических функций
Свойства тригонометрических функций Решение задач
Решение задач Примеры арифметических операций
Примеры арифметических операций Прибавить 5, 6, 7, 8, 9. Составление таблицы
Прибавить 5, 6, 7, 8, 9. Составление таблицы Факторный анализ
Факторный анализ Множественные совокупности фиктивных переменных
Множественные совокупности фиктивных переменных ТЕМА УРОКА: « Арифметическая прогрессия. Метод математической индукции.»
ТЕМА УРОКА: « Арифметическая прогрессия. Метод математической индукции.»  Векторы. Понятие вектора
Векторы. Понятие вектора Соотношения между сторонами и углами треугольника,
Соотношения между сторонами и углами треугольника, Контроль знаний учащихся на уроках математики
Контроль знаний учащихся на уроках математики Сумма углов треугольника
Сумма углов треугольника Правила вычисления производных
Правила вычисления производных Решение заданий В14 (задачи на движение) по материалам открытого банка задач ЕГЭ
Решение заданий В14 (задачи на движение) по материалам открытого банка задач ЕГЭ Математика. Игра
Математика. Игра Сложение и вычитание многочленов
Сложение и вычитание многочленов Трапеция. Свойства трапеции
Трапеция. Свойства трапеции Равнобедренный треугольник, его свойства
Равнобедренный треугольник, его свойства Лекция 04. О термине «Геометрия»
Лекция 04. О термине «Геометрия» Умножение и деление обыкновенных дробей. Математический диктант
Умножение и деление обыкновенных дробей. Математический диктант УЧИМ СОСТАВ ЧИСЛА от 5 до 10 Автор презентации и текста: Бойкова О.В., учитель начальных классов МОУ СОШ №1 Г. Конаково Тверской о
УЧИМ СОСТАВ ЧИСЛА от 5 до 10 Автор презентации и текста: Бойкова О.В., учитель начальных классов МОУ СОШ №1 Г. Конаково Тверской о