Содержание
- 2. 1. Определитель матрицы, его свойства, методы нахождения определителя Рассмотрим квадратную матрицу второго порядка. Определителем этой матрицы
- 3. Определитель матрицы, его свойства, методы нахождения определителя Определителем матрицы третьего порядка называют число, которое находят с
- 4. Вычисление определителя Пример:
- 5. Разложение определителя по элементам строки (столбца) Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие
- 6. Разложение определителя по элементам строки (столбца) Минором элемента определителя называется определитель, получаемый из данного путем вычеркивания
- 7. Разложение определителя по элементам первой строки Аналогичным образом определитель третьего порядка может быть разложен по элементам
- 8. Разложение определителя по элементам строки (столбца) Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где: 1) нулей
- 9. Свойства определителей 1. При транспонировании матрицы величина её определителя не меняется 2. Если две строки (или
- 10. Обратная матрица. Ранг матрицы Матрицей, обратной к матрице А, называется квадратная матрица A-1, такая что A-1
- 11. Пример Найти матрицу, обратную данной: Вычислим определитель: Находим А-1: Проверка:
- 12. Ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимается: - замена строк столбцами, а
- 13. Вычисление ранга матрицы Вычтем из 2-ой строки 1-ую строку, к 3-ей прибавляем 1-ую строку, умноженную на
- 15. Скачать презентацию












 Теория вероятностей и элементы математической статистики
Теория вероятностей и элементы математической статистики Деление обыкновенных дробей
Деление обыкновенных дробей Страницы для любознательных. Часть 1. (1 ласс)
Страницы для любознательных. Часть 1. (1 ласс)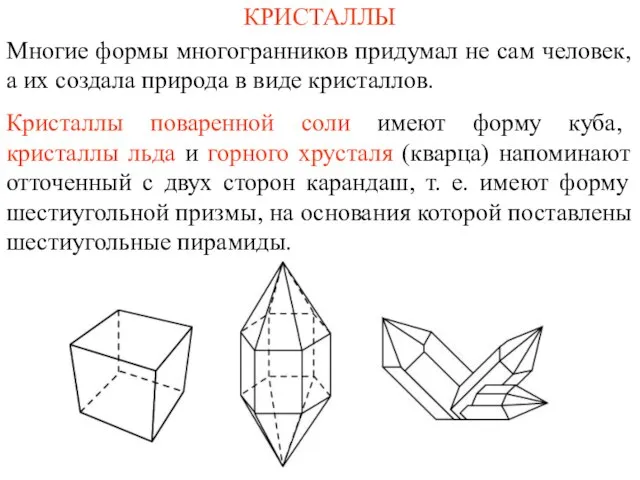 Кристалы - природные многогранники
Кристалы - природные многогранники Числа 1, 2, 3. Знаки +, -, =
Числа 1, 2, 3. Знаки +, -, = Движения
Движения Квадратные уравнения и различные способы их решения
Квадратные уравнения и различные способы их решения 3D моделирование на уроках стереометрии
3D моделирование на уроках стереометрии Натуральные числа. Урок-путешествие в 5-м классе
Натуральные числа. Урок-путешествие в 5-м классе Пирамида
Пирамида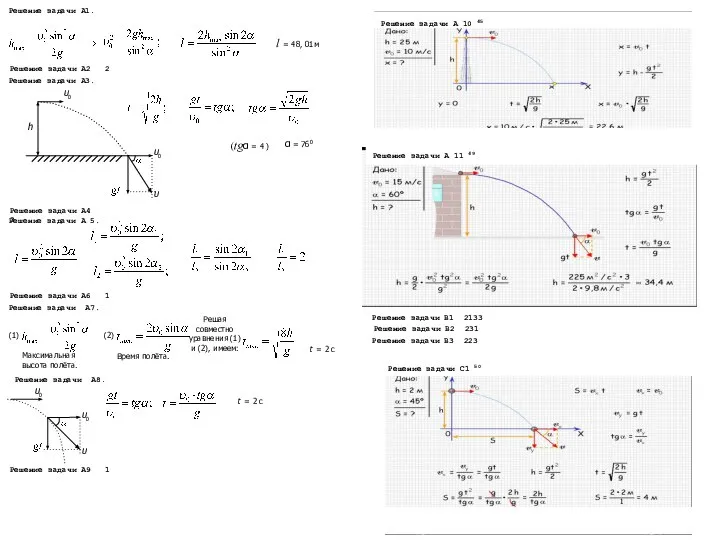 Ответы и решения.Решение задачи А1
Ответы и решения.Решение задачи А1 Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Повторение. Начальные геометрические сведения
Повторение. Начальные геометрические сведения Логарифмические неравенства
Логарифмические неравенства Тема: Построение равнобедренного треугольник по длине его основания и боковой стороне Автор презентации учитель математики
Тема: Построение равнобедренного треугольник по длине его основания и боковой стороне Автор презентации учитель математики  Считаем в уме
Считаем в уме Комплексный экзамен. Математика
Комплексный экзамен. Математика Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл
Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл Задания В9
Задания В9 Цифра 10
Цифра 10 Вычитание из чисел 8 и 9. Состав 8 и 9
Вычитание из чисел 8 и 9. Состав 8 и 9 23. Признак перпендикулярности двух плоскостей
23. Признак перпендикулярности двух плоскостей Способы решения систем уравнений (5)
Способы решения систем уравнений (5) Співнапрямлені промені
Співнапрямлені промені Анализ временных рядов
Анализ временных рядов Конус
Конус Исследовательская работа по теме «Арифметика» Л.Ф. Магницкого. Задачи на сплавы и смеси». Выполнила Чистякова Надежда Ученица 8 «В
Исследовательская работа по теме «Арифметика» Л.Ф. Магницкого. Задачи на сплавы и смеси». Выполнила Чистякова Надежда Ученица 8 «В Логарифмы и их свойства. Готовимся к ЕГЭ
Логарифмы и их свойства. Готовимся к ЕГЭ