Содержание
- 2. Содержание. 1.Определения: 1.1.Преобразование фигур. 2.2.Отображение плоскости на себя. 1.3.Движение фигуры. 1.4.Движение плоскости. 1.5.Гомотетия. 2.Задача на усвоение
- 3. Содержание. 5.Центральная симметрия. 5.1.Построение симметричных точек и отрезков. 5.2.Центральная симметрия в системе координат. 5.3.Задача на построение.
- 4. Определения. Преобразование фигур. Движение фигур. Отображение плоскости на себя. Движение плоскости.
- 5. Фигура F' получена преобразованием фигуры F. Фигура F' является образом фигуры F при данном преобразовании. Фигуру
- 6. Пример преобразования фигуры: Сжатие к оси X: Если каждой точке М(x,y) ставим в соответствие М'(x',y') и
- 7. Отображение плоскости на себя. Если 1) каждой точке плоскости сопоставляется какая-то одна точка этой же плоскости,
- 8. Пример соответствия между точками плоскости, не являющимся отображением плоскости на себя: Ортогональная проекция каждой точки плоскости
- 9. Движения фигур. Преобразование фигуры, сохраняющее расстояние между точками, называют движением фигуры. При таком преобразовании фигуры сохраняются
- 10. Движение плоскости- отображение плоскости на себя, которое сохраняет расстояния между точками. Отрезок движением переводится в отрезок.
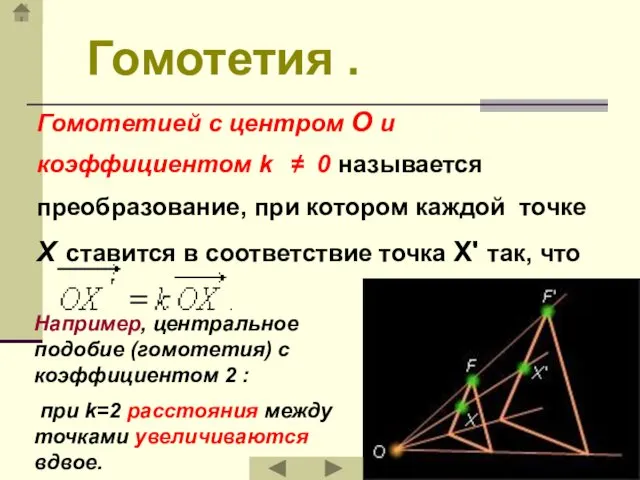
- 11. Гомотетия . Гомотетией с центром O и коэффициентом k ≠ 0 называется преобразование, при котором каждой
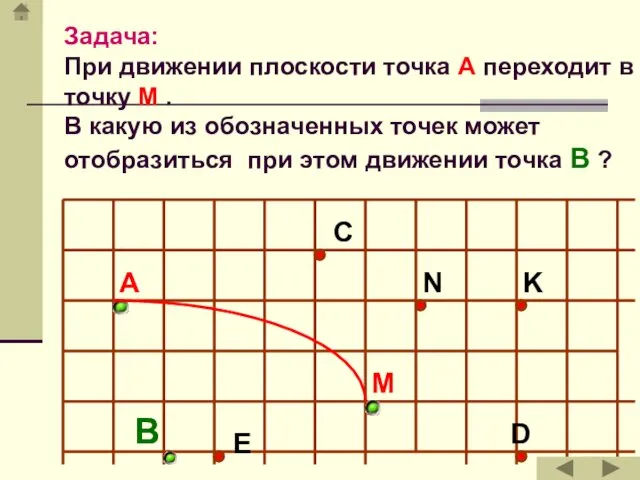
- 12. Задача: При движении плоскости точка А переходит в точку М . В какую из обозначенных точек
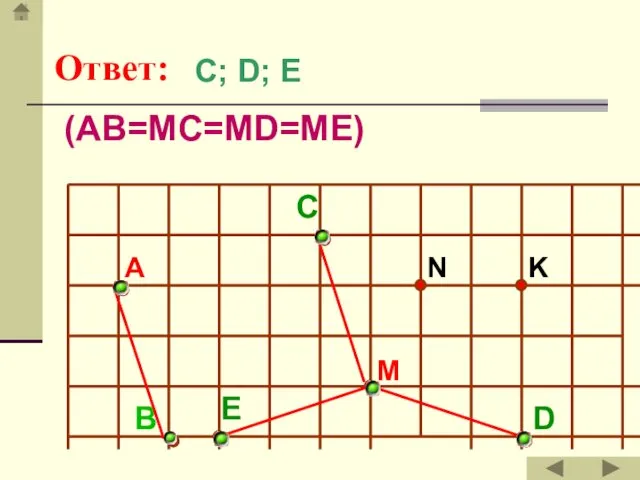
- 13. Ответ: А C N K M B E D С; D; E (AB=MC=MD=ME)
- 14. Основные виды движений: Осевая Осевая и центральная Осевая и центральная симметрии Поворот Параллельный перенос
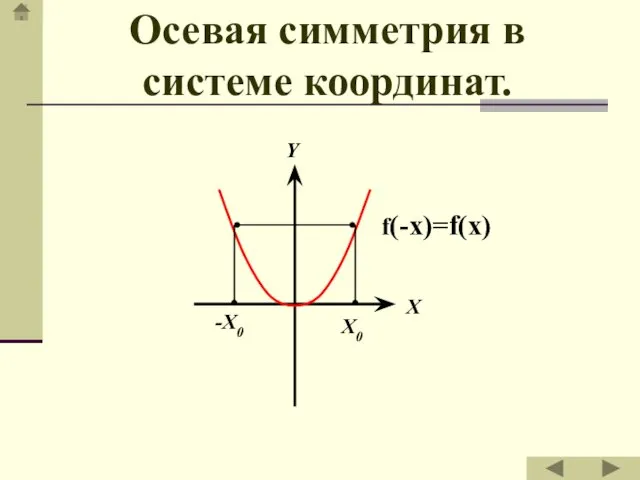
- 15. Точки X и X' называются симметричными относительно прямой a, и каждая из них – симметричной другой,
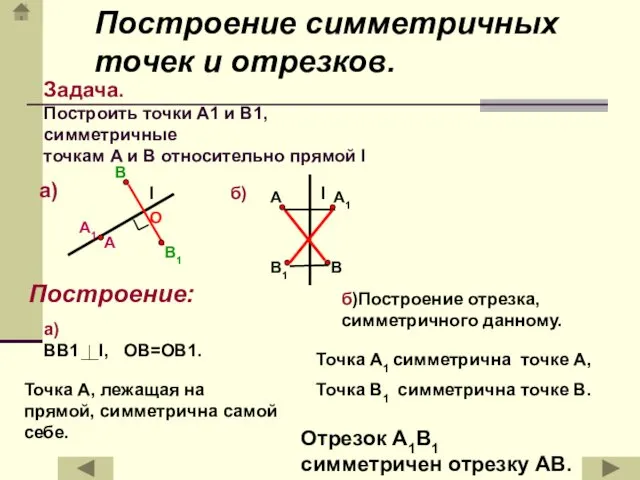
- 16. l а) A1 l б) В1 Задача. Построить точки А1 и B1, симметричные точкам А и
- 17. Осевой симметрией с осью a называется такое преобразование фигуры ,при котором каждой точке данной фигуры сопоставляется
- 18. Осевая симметрия является движением . Почему отображение, сохраняющее расстояния, называется движением? Это можно пояснить на примере
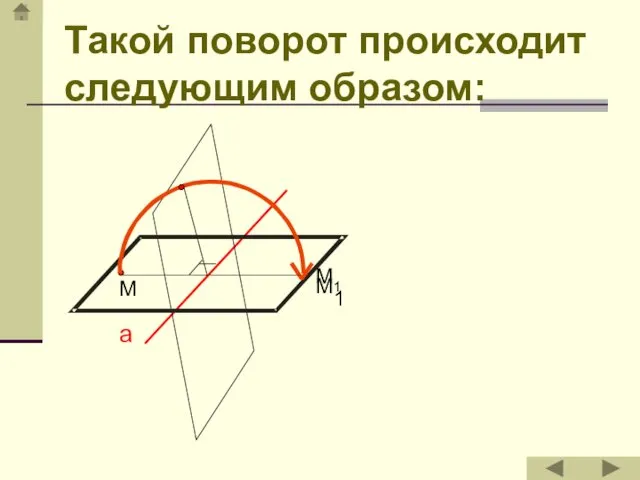
- 19. а М1 Такой поворот происходит следующим образом:
- 20. Осевая симметрия в системе координат.
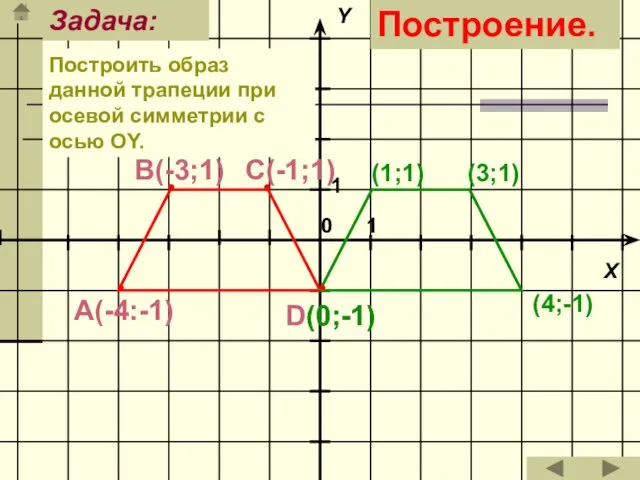
- 21. Построить образ данной трапеции при осевой симметрии с осью ОY. Задача: (3;1) (1;1) (0;-1) (4;-1) Построение.
- 22. Симметрия фигуры. Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричная ей точка
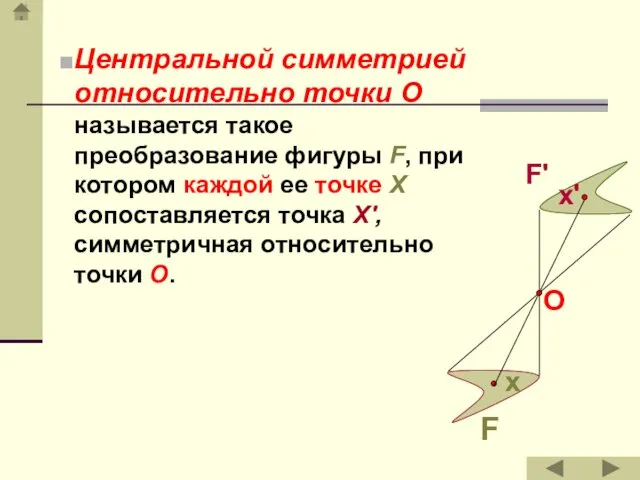
- 23. Точки X и Х' называются симметричными относительно заданной точки O, если ОХ=ОХ', а лучи OX и
- 24. Центральной симметрией относительно точки O называется такое преобразование фигуры F, при котором каждой ее точке X
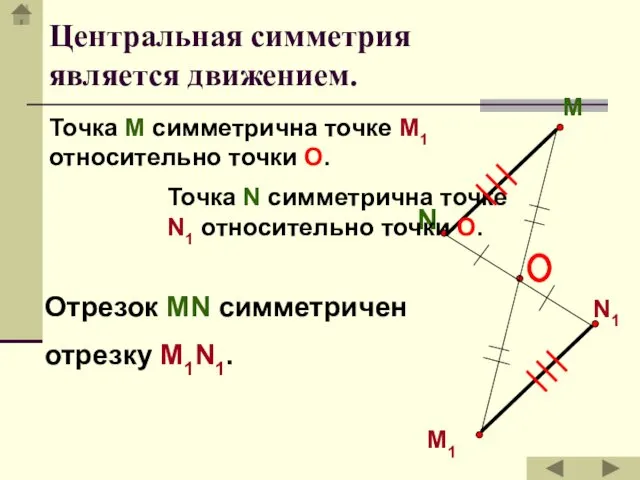
- 25. M N N1 M1 Точка М симметрична точке М1 относительно точки О. Точка N симметрична точке
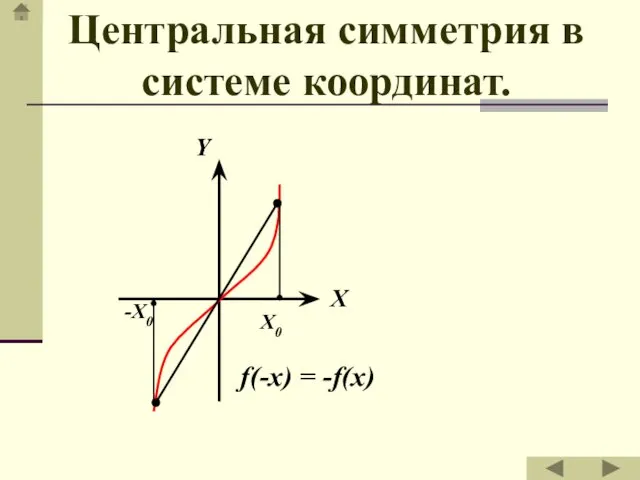
- 26. Центральная симметрия в системе координат.
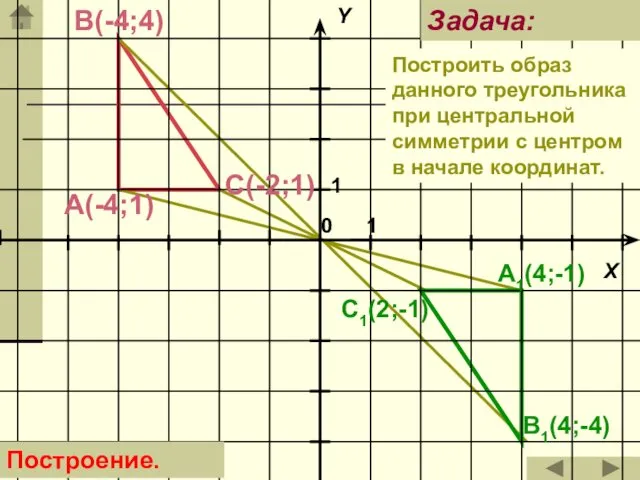
- 27. B1(4;-4) С(-2;1) A1(4;-1) C1(2;-1) А(-4;1) В(-4;4) Задача: Построение. Построить образ данного треугольника при центральной симметрии с
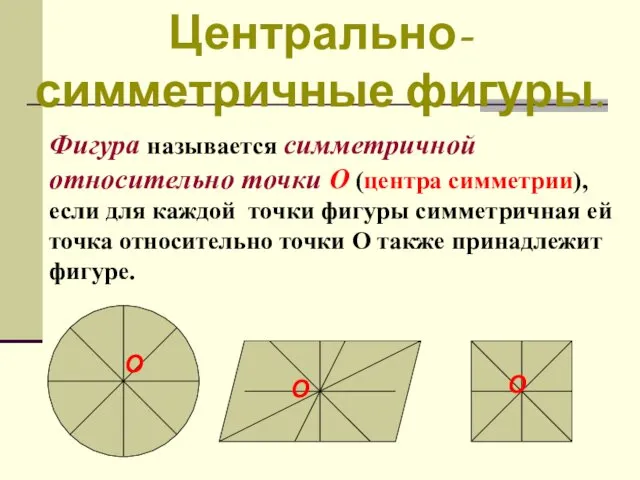
- 28. Центрально-симметричные фигуры. Фигура называется симметричной относительно точки О (центра симметрии), если для каждой точки фигуры симметричная
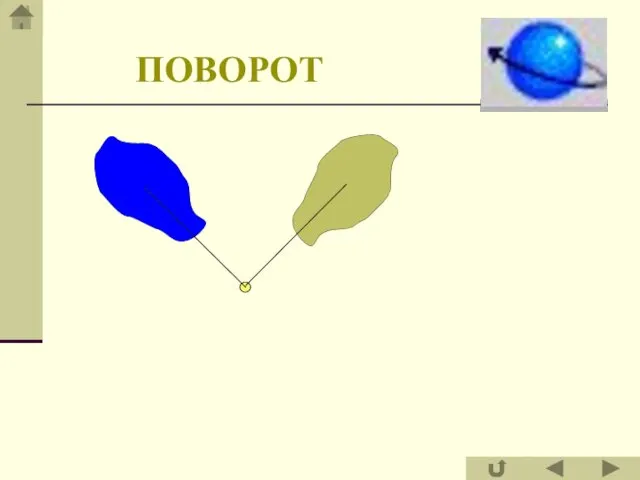
- 29. ПОВОРОТ
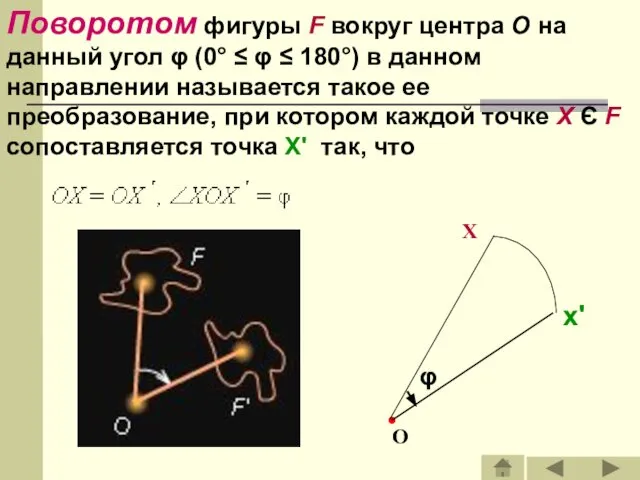
- 30. Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°) в
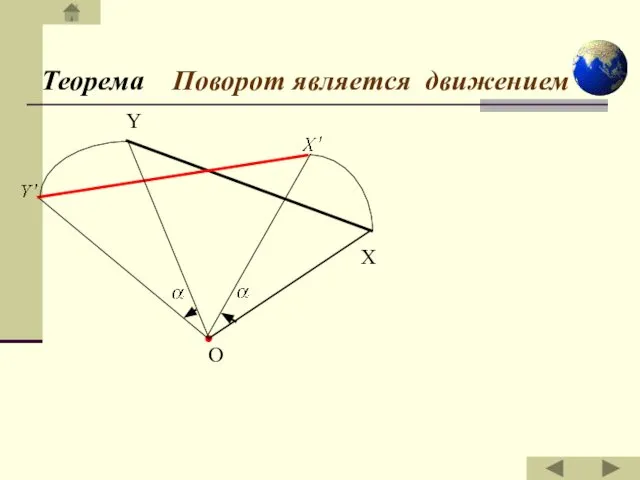
- 31. Теорема Поворот является движением О Y X
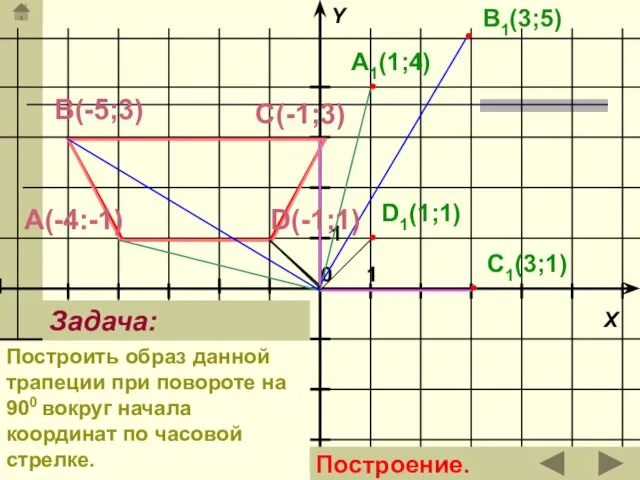
- 32. А(-4:-1) В(-5;3) D(-1;1) С(-1;3) A1(1;4) B1(3;5) C1(3;1) D1(1;1) Задача: Построить образ данной трапеции при повороте на
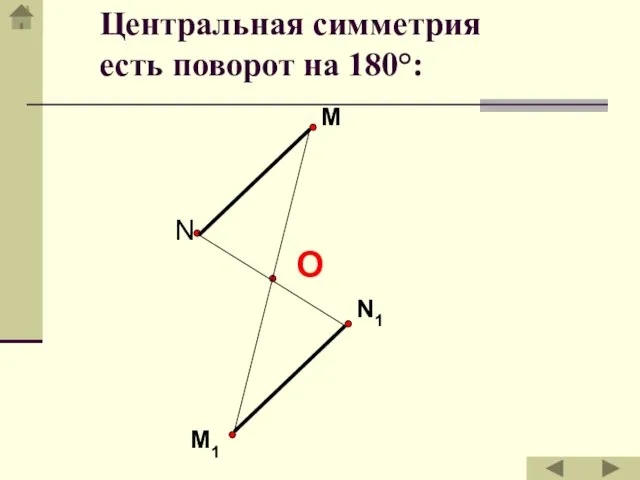
- 33. M N N1 M1 Центральная симметрия есть поворот на 180°: О
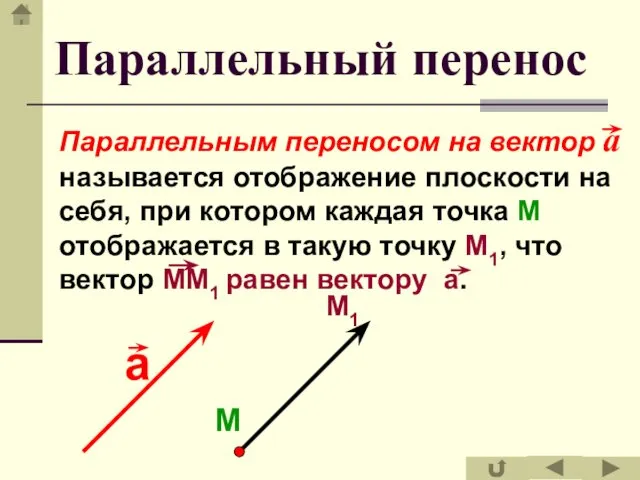
- 34. Параллельный перенос Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка
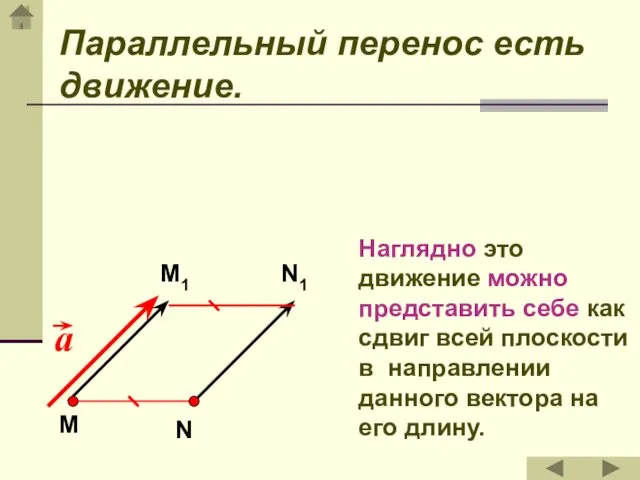
- 35. Параллельный перенос есть движение. Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении
- 36. Параллельный перенос на плоскости в системе координат. Введем на плоскости систему координат O, X, Y. Преобразование
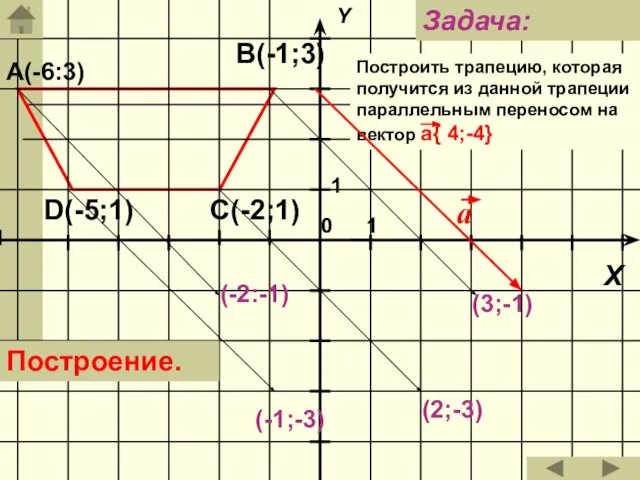
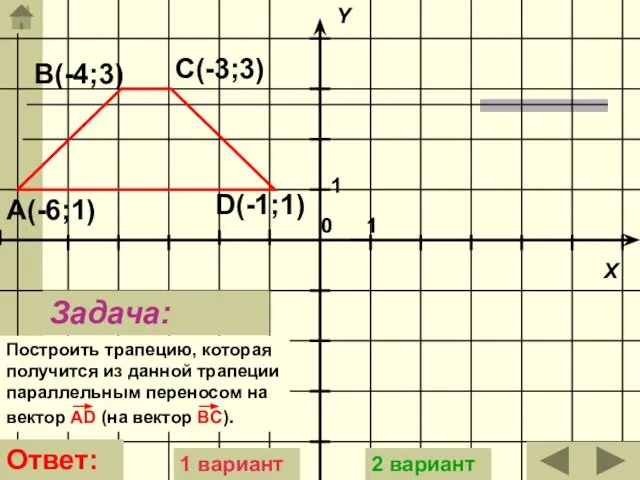
- 37. А(-6:3) В(-1;3) С(-2;1) D(-5;1) Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор а{
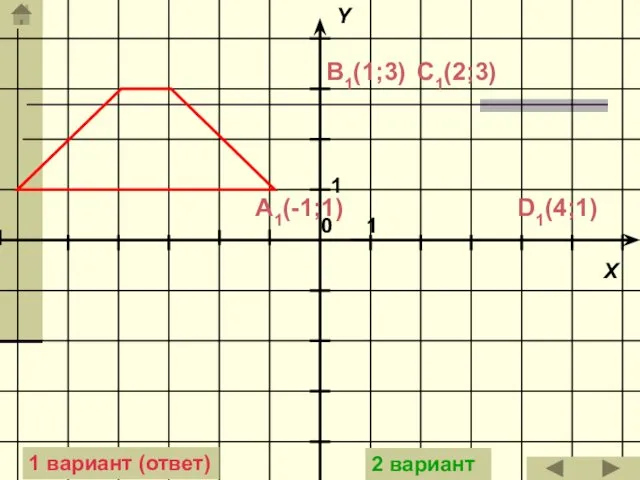
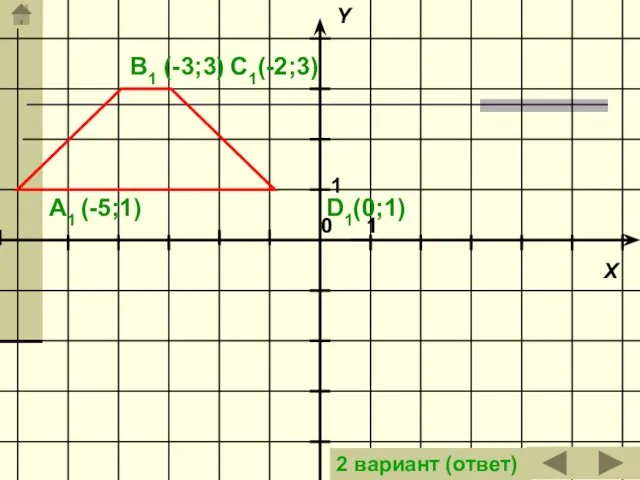
- 38. Задача: Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор АD (на вектор BC).
- 39. C1(2;3) D1(4;1) B1(1;3) A1(-1;1) 1 вариант (ответ) 2 вариант
- 40. A1 (-5;1) B1 (-3;3) C1(-2;3) D1(0;1) 2 вариант (ответ)
- 41. Урок окончен. Спасибо за внимание.
- 42. Раздаточный материал.
- 44. Скачать презентацию


















 Математическая шкатулка! Учимся отгадывать ребусы
Математическая шкатулка! Учимся отгадывать ребусы Многогранники. Призма и её основные элементы. Построение сечений
Многогранники. Призма и её основные элементы. Построение сечений Понятие числовой окружности. Радианное измерение углов
Понятие числовой окружности. Радианное измерение углов О подготовке к ЕГЭ по математике 2013 Шноль Дмитрий Эммануилович, Зав. кафедрой математики школы «Интеллектуал», методист МИО
О подготовке к ЕГЭ по математике 2013 Шноль Дмитрий Эммануилович, Зав. кафедрой математики школы «Интеллектуал», методист МИО Метрологическое обеспечение производства по переработке мясных продуктов
Метрологическое обеспечение производства по переработке мясных продуктов Сложение и вычитание чисел в пределах 10
Сложение и вычитание чисел в пределах 10 Формулы сокращенного умножения
Формулы сокращенного умножения Анализ временных рядов
Анализ временных рядов Группировка материала статистических наблюдений
Группировка материала статистических наблюдений Презентация на тему Математические задачи от русских, советских и зарубежных писателей
Презентация на тему Математические задачи от русских, советских и зарубежных писателей  Геометрия древесного ствола
Геометрия древесного ствола Геометрические иллюзии, или всегда ли мы видим то, что видим
Геометрические иллюзии, или всегда ли мы видим то, что видим Параллельные плоскости. Задачи
Параллельные плоскости. Задачи выполнила: ученица 7-го класса Третьякова Люда
выполнила: ученица 7-го класса Третьякова Люда Геометрия. Точка и прямая
Геометрия. Точка и прямая Теорема синусов
Теорема синусов Геометрические тела и их проекции
Геометрические тела и их проекции Презентация по математике "Своя игра "Одночлены и многочлены"" - скачать
Презентация по математике "Своя игра "Одночлены и многочлены"" - скачать  Презентация по математике "Единицы площади урок" - скачать
Презентация по математике "Единицы площади урок" - скачать  Распределительный закон умножения
Распределительный закон умножения Геометрическая оптика. Введение
Геометрическая оптика. Введение Функция. График функции
Функция. График функции Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Свойства и признаки параллелограмма
Свойства и признаки параллелограмма Производная функции. Алгебра, 10 класс
Производная функции. Алгебра, 10 класс Доли. Обыкновенные дроби
Доли. Обыкновенные дроби linear octree
linear octree Кратные и двойные интегралы
Кратные и двойные интегралы