Основы фрактальной теории, знакомство с математическим обоснованием графической интерпретации фрактальных образов
Содержание
- 2. ЦЕЛЬ РАБОТЫ исследование и изучение основ фрактальной теории, знакомство с математическим обоснованием графической интерпретации фрактальных образов
- 3. ОСНОВНЫЕ НАПРАВЛЕНИЯ РАБОТЫ История появления Определение фрактала Примеры фракталов Классификация фракталов Применение фракталов Заключение Фракталы в
- 4. Фрактал - геометрическая фигура, состоящая из частей, которые могут быть поделены на части, каждая из которых
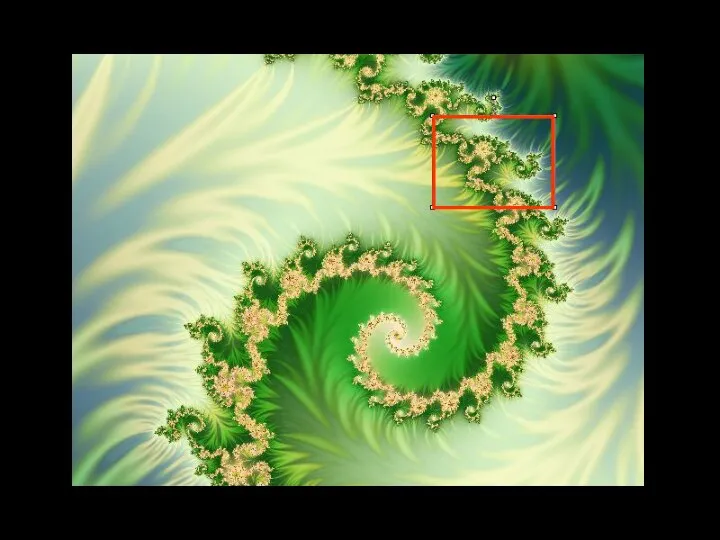
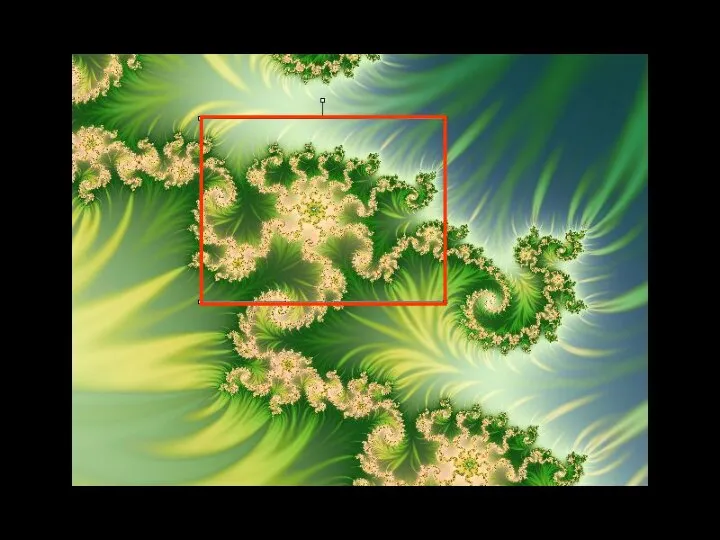
- 8. ФРАКТАЛЫ В ПРИРОДЕ
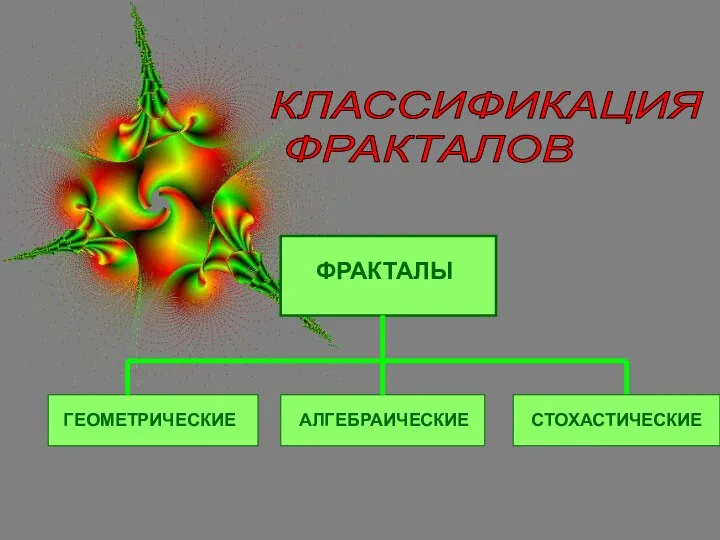
- 9. КЛАССИФИКАЦИЯ ФРАКТАЛОВ ГЕОМЕТРИЧЕСКИЕ
- 10. Это «функции - монстры», которых так называли за недифференцируемость в каждой точке. Геометрические фракталы являются также
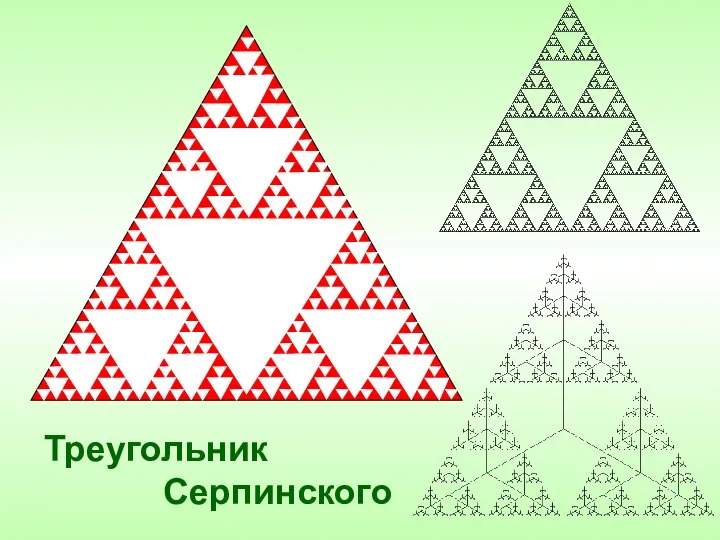
- 11. Треугольник Серпинского
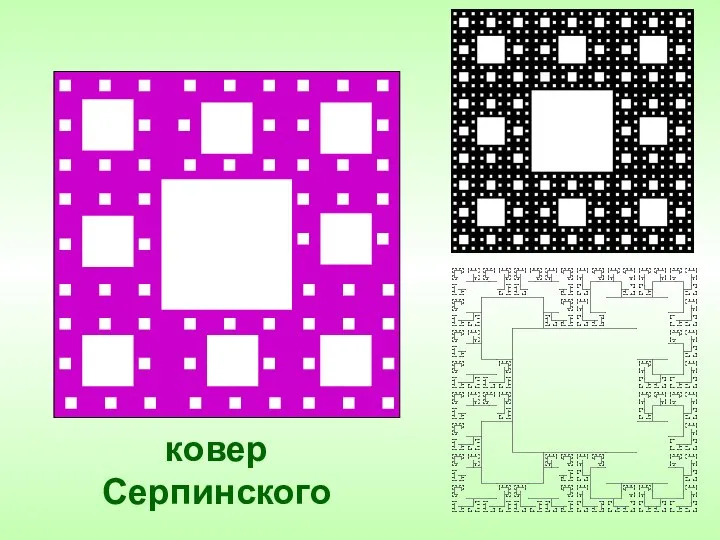
- 12. ковер Серпинского
- 15. Это фракталы, которые можно построить, используя простые алгебраические формулы. Получают их с помощью нелинейных процессов в
- 16. Множество Жюлиа Цвет каждой точки зависит от того, сколько итераций комплексной функции может быть сделано, пока
- 17. МНОЖЕСТВО МАНДЕЛЬБРОТА (окрашено лиловым цветом). Картинка получается с помощью той же процедуры, что и выше. Различие
- 18. Если выбрать показатель степени комплексного числа в виде любого натурального числа n, то получим многочисленный класс
- 20. Это фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры. Эти фракталы используются
- 23. Скачать презентацию












 Графическое решение задачи линейного программирования с двумя переменными
Графическое решение задачи линейного программирования с двумя переменными Длина отрезка
Длина отрезка Композиция чертежа. Проецирование Урок черчения в 8 классе
Композиция чертежа. Проецирование Урок черчения в 8 классе Формулы суммы и разности синуса и косинуса
Формулы суммы и разности синуса и косинуса Дискретные структуы. Теория графов. Основные понятия
Дискретные структуы. Теория графов. Основные понятия Урок математики, 2 класс «Проверка вычитания»
Урок математики, 2 класс «Проверка вычитания» Икосаэдр
Икосаэдр Похідна функції, її геометричний та фізичний зміст
Похідна функції, її геометричний та фізичний зміст Развитие логического мышления младших школьников посредством решения нестандартных задач
Развитие логического мышления младших школьников посредством решения нестандартных задач Ітераційні методи розв’язування СЛАР (Система лінійних алгебраїчних рівнянь)
Ітераційні методи розв’язування СЛАР (Система лінійних алгебраїчних рівнянь) Система линейных уравнений с двумя переменными
Система линейных уравнений с двумя переменными Решение задач по теме Окружность
Решение задач по теме Окружность Задачи со спичками
Задачи со спичками КВН. Математика повсюду!!! Попкова Виктория Юрьевна Учитель математики, г.Сургут
КВН. Математика повсюду!!! Попкова Виктория Юрьевна Учитель математики, г.Сургут  Степень с целым показателем
Степень с целым показателем Математичне моделювання кінцевих стохастичних процесів
Математичне моделювання кінцевих стохастичних процесів Вероятность совместных и несовместных событий
Вероятность совместных и несовместных событий Четырехугольники. Проверочная работа по чертежам
Четырехугольники. Проверочная работа по чертежам «Прямая пропорциональность» Урок математики в 7 классе Автор: Еремеева Марина Леонидовна Учитель математики МОУ «Гимназия№
«Прямая пропорциональность» Урок математики в 7 классе Автор: Еремеева Марина Леонидовна Учитель математики МОУ «Гимназия№ Действия с положительными и отрицательными числами
Действия с положительными и отрицательными числами Полный стрелочный угол
Полный стрелочный угол Геометрическое место точек. Окружность и круг
Геометрическое место точек. Окружность и круг Урок математики Вычитание с переходом через десяток
Урок математики Вычитание с переходом через десяток  Симметрия. Центральная симметрия
Симметрия. Центральная симметрия Фракталы в биологии
Фракталы в биологии Кривые 2-го порядка
Кривые 2-го порядка Нахождение числа по его дроби. 6 класс
Нахождение числа по его дроби. 6 класс Измерение размеров деталей с помощью штангенциркуля
Измерение размеров деталей с помощью штангенциркуля