Содержание
- 2. Две прямые называются параллельными, если они не пересекаются. b a Обозначают: a || b
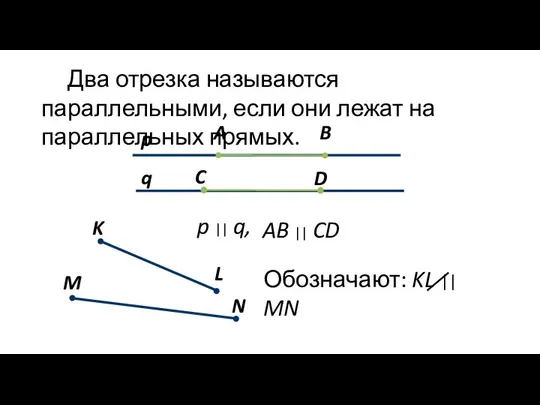
- 3. Два отрезка называются параллельными, если они лежат на параллельных прямых. q p B A D p
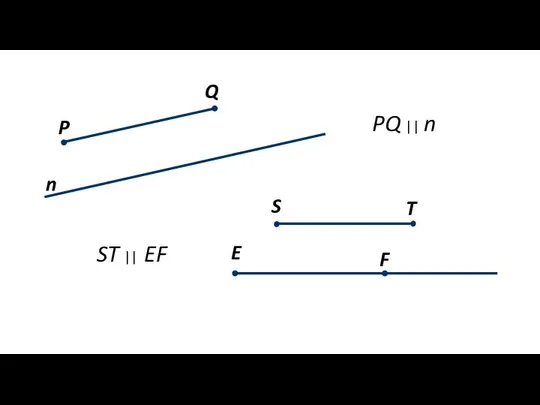
- 4. Q P n PQ || n T S E F ST || EF
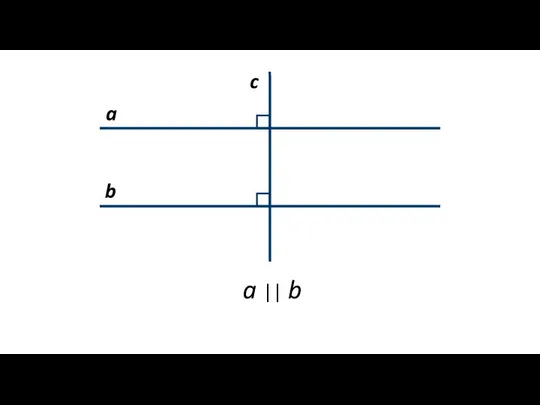
- 5. a b c a || b
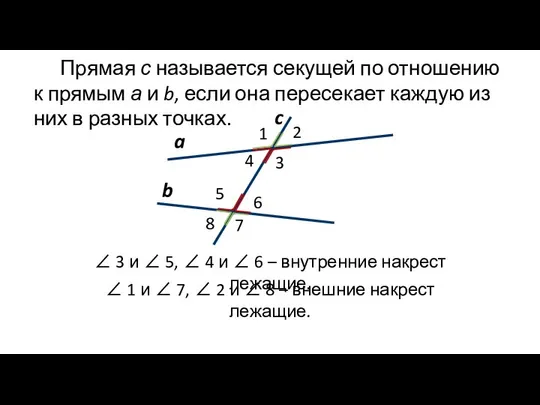
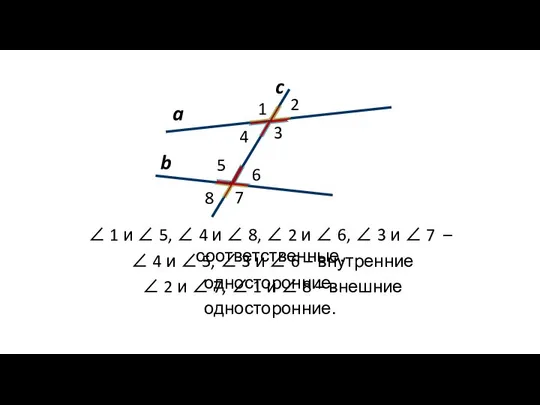
- 6. 1 3 4 2 5 6 7 8 ∠ 3 и ∠ 5, ∠ 4 и
- 7. a b c 1 3 4 2 5 6 7 8 ∠ 4 и ∠ 5,
- 8. Теорема. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Доказательство. Если
- 9. Задача. Докажите, что если два отрезка KL и MN равны и параллельны, то отрезки КМ и
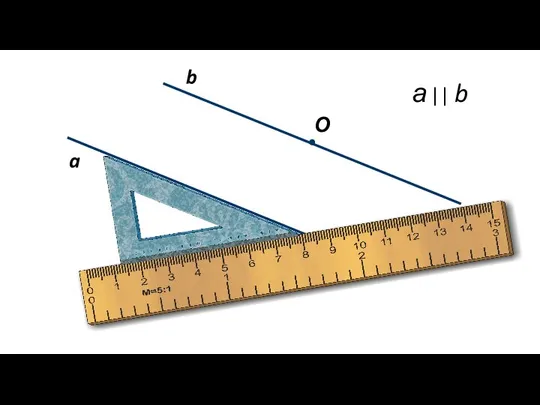
- 10. а || b
- 11. Рейсшина
- 13. Скачать презентацию



 Тренажёр «Многозначные числа»
Тренажёр «Многозначные числа» Решение задач с помощью уравнений
Решение задач с помощью уравнений Занимательные задачи
Занимательные задачи Формулы сокращенного умножения
Формулы сокращенного умножения Графики линейной функции
Графики линейной функции Великие математики древности МБОУ «Авиловская СОШ» Учитель математики Ткаченко И.А.
Великие математики древности МБОУ «Авиловская СОШ» Учитель математики Ткаченко И.А. Применение теории графов к решению задач
Применение теории графов к решению задач Статистикалық болжамды тексеру
Статистикалық болжамды тексеру Презентация по математике "О теореме Пифагора и способах её доказательства" - скачать
Презентация по математике "О теореме Пифагора и способах её доказательства" - скачать  Алгебра. Лекция 6. Классы вычетов
Алгебра. Лекция 6. Классы вычетов Спецификация переменных в уравнениях регрессии
Спецификация переменных в уравнениях регрессии Произведение двух последовательных отрицательных чисел
Произведение двух последовательных отрицательных чисел Логика. Введение
Логика. Введение Урок математики в 6 классе по теме: «Действия над дробями» Методическая разработка учителя математики МОУ Гимназия №111 г.Уфы
Урок математики в 6 классе по теме: «Действия над дробями» Методическая разработка учителя математики МОУ Гимназия №111 г.Уфы  Понятие площади фигуры и её измерение. Что такое площадь. Свойства площади. Какие фигуры называют равными. Какие фигуры называют
Понятие площади фигуры и её измерение. Что такое площадь. Свойства площади. Какие фигуры называют равными. Какие фигуры называют  Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Презентация по математике "«Чётные и нечётные функции»" - скачать бесплатно_
Презентация по математике "«Чётные и нечётные функции»" - скачать бесплатно_ Геометрические тела вокруг нас
Геометрические тела вокруг нас Производные и интегралы функций общего вида
Производные и интегралы функций общего вида Сочетательное и распределительное свойство умножения
Сочетательное и распределительное свойство умножения Пропорция
Пропорция Признак параллельности прямых по равенству соответственных углов
Признак параллельности прямых по равенству соответственных углов Весёлые человечки спешат на помощь. Занятие для дошкольников
Весёлые человечки спешат на помощь. Занятие для дошкольников Интегральные исчисления
Интегральные исчисления Связь между компонентами и результатом умножения
Связь между компонентами и результатом умножения Многоугольник. Задачи и упражнения
Многоугольник. Задачи и упражнения Площадь треугольника и высоты
Площадь треугольника и высоты Регрессионный анализ
Регрессионный анализ