Первообразная и интеграл

Первообразная
(повторение)

Определение

Функция F(х) называется первообразной функции f(х) на промежутке Х, если
На

Теорема 1

Если функция f(х) непрерывна при
, то для f(х)

Теорема 2

Если F(x) одна из первообразных функции f(x), на промежутке Х,

Таблица первообразных

Зная формулы для нахождения производных, можно составить таблицу для

Правила нахождения первообразных

Первообразная суммы равна сумме первообразных
Если F(x) – первообразная для

1.Проверь себя. Соотнеси выражения в правом и левом столбцах

Если f(x) равно:
1)

2. Ответить на вопрос: какая функция является перообразной для функции f(x)=

3. Выберите ответ, при котором предложение будет верно.

Функция F(x) является

4. Ответить на вопрос: для какой функции первообразной является функция F(x)=2x³+6x²+x-9?

А)

5. Ответить на вопрос: производная какой из функций равна у =

Записать в тетрадь.
Примеры с решениями

Задание №1. Найдите первообразную функции f(x), график которой проходит через точку

б) f(x)=3х - 5, А(4;10)
Решение.
F(x)= 3х²⁄2-5х+С, где С –

Выполни самостоятельно

Найдите первообразную функции f(x), график которой проходит через точку А,

Задание №2. Найдите первообразную функции f(x), значение которой при х =

б) f(x)=2sin3x+4cos(x/2); х₀=π⁄3; у₀=0

Решение.
F(x)=-2·1/3·cos3x+4·2 sin(x/2)+С=
=-2/3·cos3x+8· sin(x/2)+С, где С- пр. ч.
Найдём

в) f(x)=4+6х²; х₀=2; у₀<0

Решение. F(x)= 4х+6х³⁄3+С, где С-п.ч.
Найдём С:

г) f(x)=2х³+х²+3; х₀=1; у₀>0

Решение.
F(x)= 2х⁴⁄4+х³⁄3+3х+С, где С- пр.ч.
Найдём С.
F(1)=

ИНТЕГРАЛЫ

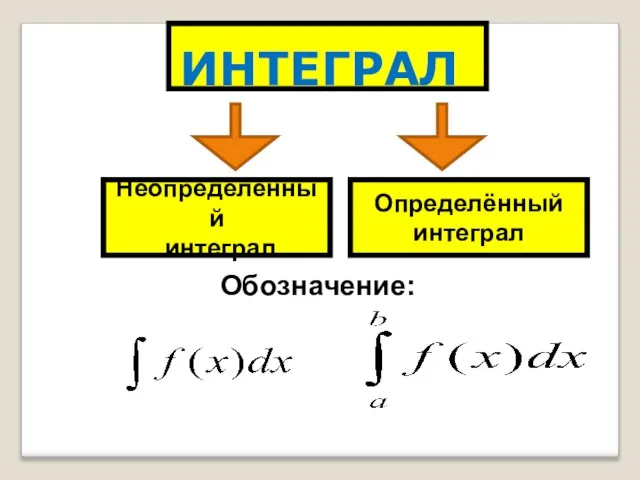
ИНТЕГРАЛ
Неопределённый
интеграл
Определённый
интеграл

Обозначение:

НЕОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛ

Определение:

Множество всех первообразных функции f(x) на некотором промежутке называется неопределенным интегралом

Таблица интегралов

Определение

Процесс нахождения интеграла называется интегрированием.
Интегрирование является операцией, обратной 
дифференцированию

Историческая справка

Интегрирование прослеживается еще в древнем Египте, примерно в 1800 г.

Историческая справка

метод исчерпывания Евдокса (примерно 370 до н.э.), который пытался

Историческая справка

Этот метод был подхвачен и развит Архимедом, и использовался

Историческая справка

Аналогичные методы были разработаны не зависимо в Китае в

Историческая справка

Этот метод впоследствии использовали Цзу Чунжи и Цзу Гэн для

Историческая справка

Следующий крупный шаг в исследование интегралов был сделан в Ираке,

Новая тема. Всё записать в тетрадь

ОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛ

Определение

Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и

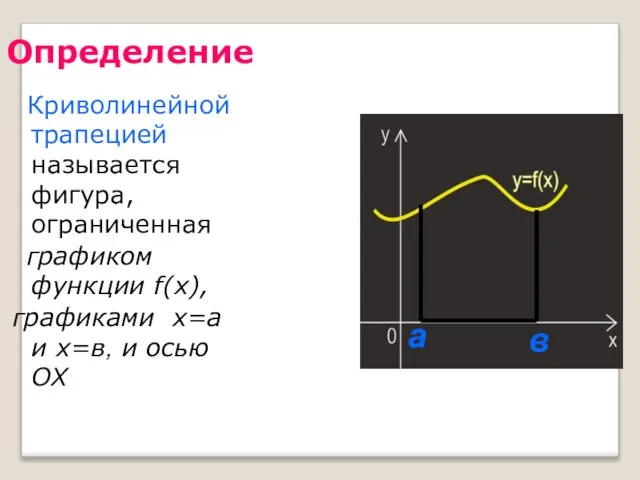
Определение

Криволинейной трапецией называется фигура, ограниченная
графиком функции f(x),
графиками

Формула Ньютона-Лейбница

Теорема: если функция у = f(x) непрерывна на отрезке [а;в],

Свойства определенного интеграла

Свойства определенного интеграла

Алгоритм вычисления площади криволинейной трапеции

Схематично изобразить график функции f(x).
Провести прямые x=a

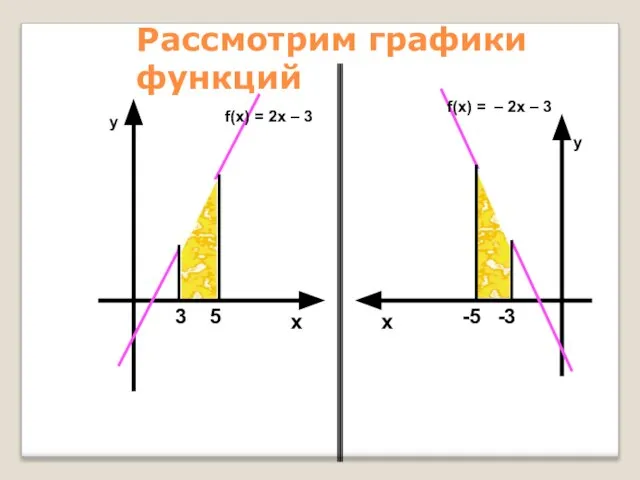
Вычислить площадь фигуры, ограниченной линиями, используя формулу Ньютона-Лейбница

Вариант 1
f(x) = 2x

Рассмотрим графики функций

f(x) = 2x – 3

f(x) = – 2x –

Запомним

Геометрический смысл определенного интеграла – это площадь криволинейной трапеции
Физический смысл определенного

Найти площадь фигуры, ограниченной линиями

1) y=–3x²–2, x=1, x=2, y=–1
2) у=