Содержание
- 2. План лекции: Задачи и методы математической статистики. Основные понятия выборочного метода. Статистическое распределение выборки. Эмпирическая функция
- 3. Актуальность темы Основные понятия и методы математической статистики необходимы для обработки результатов измерений в медицине и
- 4. Теория вероятностей занимается построением и изучением вероятностных моделей случайных явлений. Эти модели строятся на основе аналитических
- 5. Предмет математической статистики составляет разработка методов регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате
- 6. Задачи математической статистики: По результатам случайных экспериментов (выборкам) сделать содержательные выводы о вероятностных моделях, адекватно отражающих
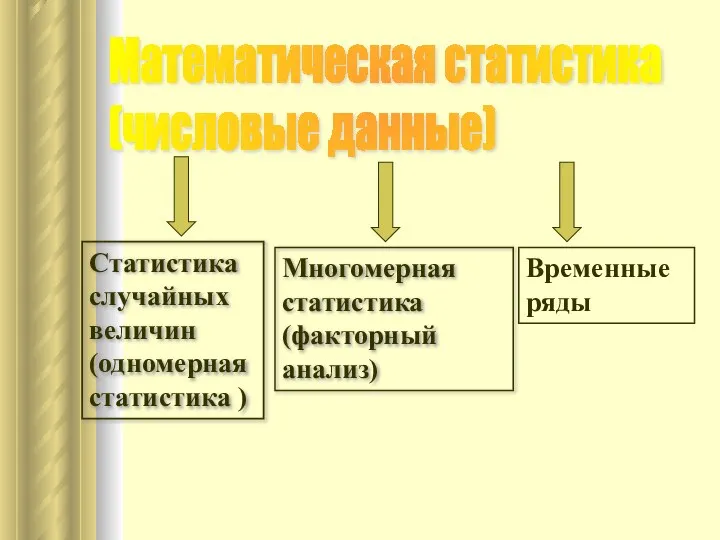
- 7. Статистика случайных величин (одномерная статистика ) Многомерная статистика (факторный анализ) Временные ряды Математическая статистика (числовые данные)
- 8. Задачи одномерной статистики Описательная статистика (представление экспериментальных данных, определение точечных и интервальных оценок) Проверка статистических гипотез
- 9. Основные понятия выборочного метода Наиболее общую совокупность, подлежащих изучению объектов называют генеральной Выборочной совокупностью или просто
- 10. Выборочные совокупности n 30 n>100 –большие Цель: С помощью статистических методов по свойствам выборки сделать вывод
- 11. Повторные Объекты возвращаются в генеральную совокупность Повторные Объекты возвращаются в генеральную совокупность Бесповторные Объекты не возвращаются
- 12. Отбор, не требующий разделения генеральной совокупности на части: Простой случайный бесповторный отбор Простой случайный повторный отбор
- 13. Типический отбор – объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части
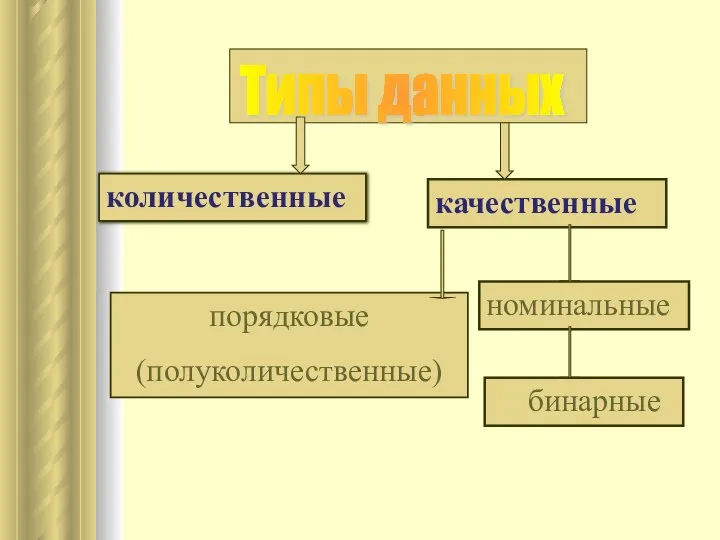
- 14. количественные качественные порядковые (полуколичественные) номинальные бинарные Типы данных
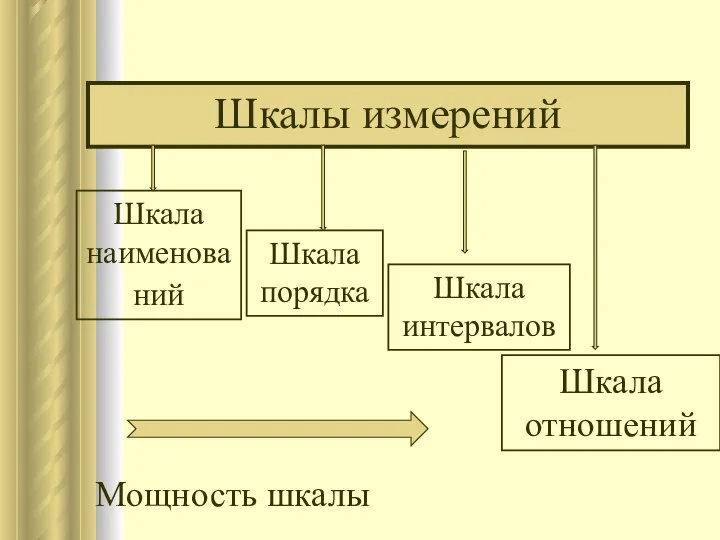
- 15. Шкалы измерений Шкала наименований Шкала порядка Шкала интервалов Шкала отношений Мощность шкалы
- 16. Шкалы и допустимые преобразования
- 17. Значения изучаемого признака называются вариантами Последовательность вариант, расположенных в возрастающем порядке называется вариационным рядом Например: 172,
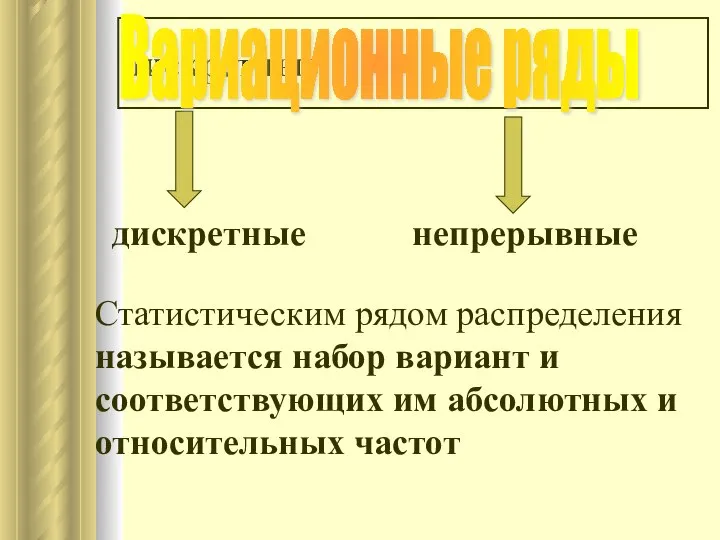
- 18. дискретные дискретные непрерывные Статистическим рядом распределения называется набор вариант и соответствующих им абсолютных и относительных частот
- 19. Статистический ряд распределения
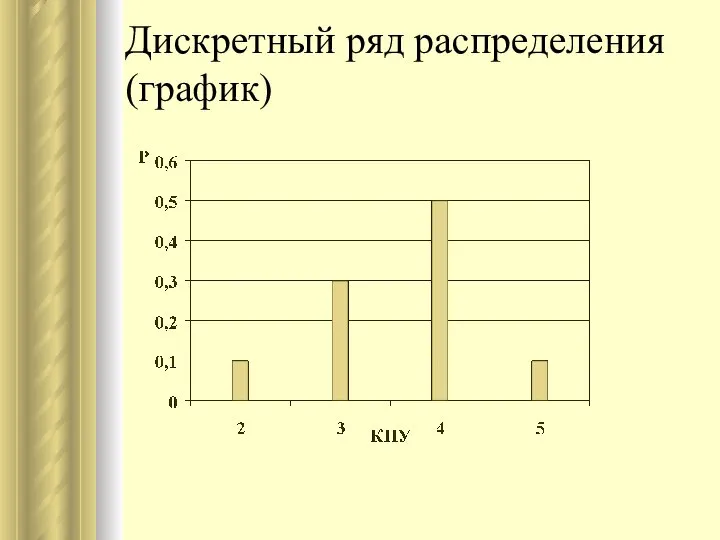
- 20. Дискретный ряд распределения (индекс КПУ) условие нормировки 2 3 4 4 2 5 4 2 3
- 21. Дискретный ряд распределения (график)
- 22. Статистическая функция распределения Пусть {х1,…,хn} - выборка наблюдений случайной величины X с функцией распределения F(x). Необходимо
- 23. Эмпирическая функция распределения имеет скачки в точках выборки (вариационного ряда), величина скачка в точке xi равна
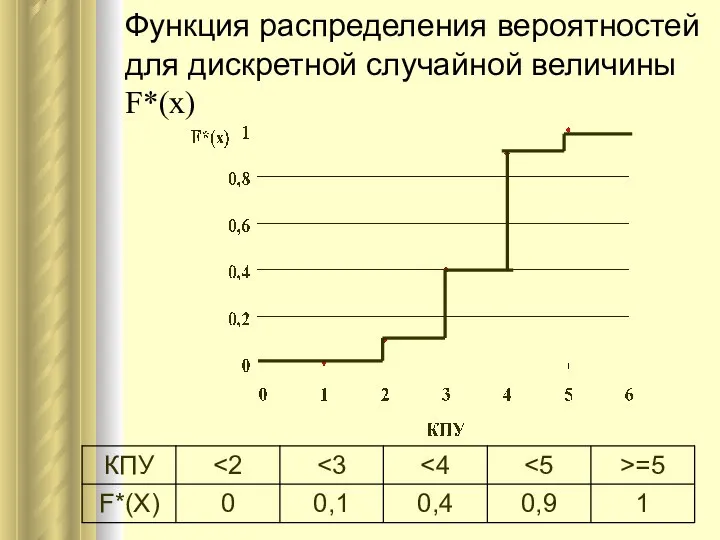
- 24. Функция распределения вероятностей для дискретной случайной величины F*(x)
- 25. Эмпирическая функция распределения
- 26. Интервальные ряды распределения Ряд распределения студентов по росту 148 158 149 162 170 156 189 151
- 27. На практике ряд распределения (вариационный ряд) составляют следующим образом: Из имеющихся значений признака x выбирают наименьшее
- 28. Интервальные ряды распределения Определяют оптимальную величину класса (интервала группировки) Эту величину также можно округлять соответственно точности
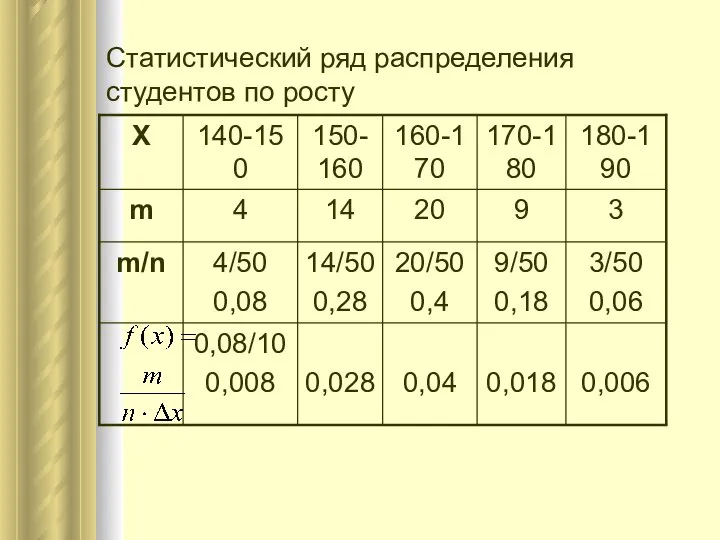
- 29. Статистический ряд распределения студентов по росту
- 30. Гистограмма распределения студентов по росту (m, m/n, f(x))
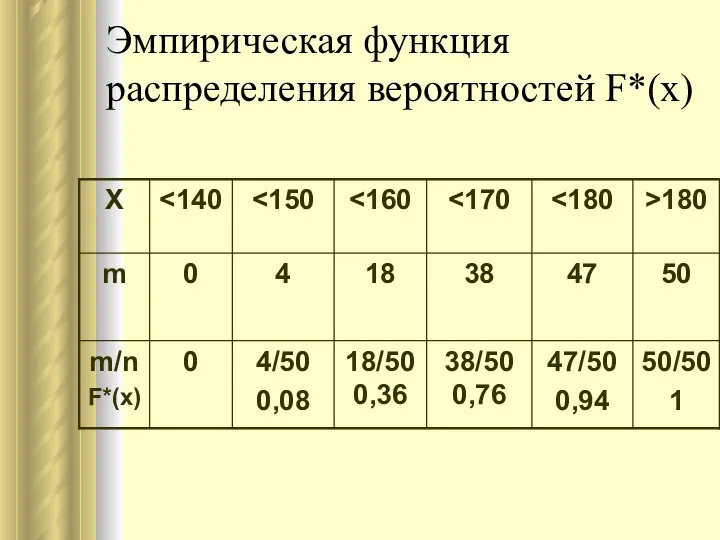
- 31. Эмпирическая функция распределения вероятностей F*(x)
- 32. Эмпирическая функция распределения F*(x)
- 33. Статистические оценки параметров распределения Задача: Изучить количественный признак генеральной совокупности. Если можно теоретически оценить вид распределения,
- 34. Пусть для изучения признака в генеральной совокупности извлечена выборка объемом n: x1, x2, x3, …, xn
- 36. В качестве оценки М(X) используется выборочное среднее: Если значения признака x1, x2, x3, …, xn имеют
- 37. Отклонением называют разность между значением признака и его средней арифметической Сумма произведений отклонений на соответствующие частоты
- 38. Оценкой D(X) служит выборочная дисперсия: 1. 2. Среднее квадратическое отклонение:
- 39. Асимметрия-скошенность распределения Эксцесс-островершинность распределения Обычно рассматривают безразмерные коэффициенты асимметрии и эксцесса:
- 40. Коэффициент вариации Характеризует относительное значение среднего квадратического отклонения и служит для сравнения разброса несоизмеримых показателей
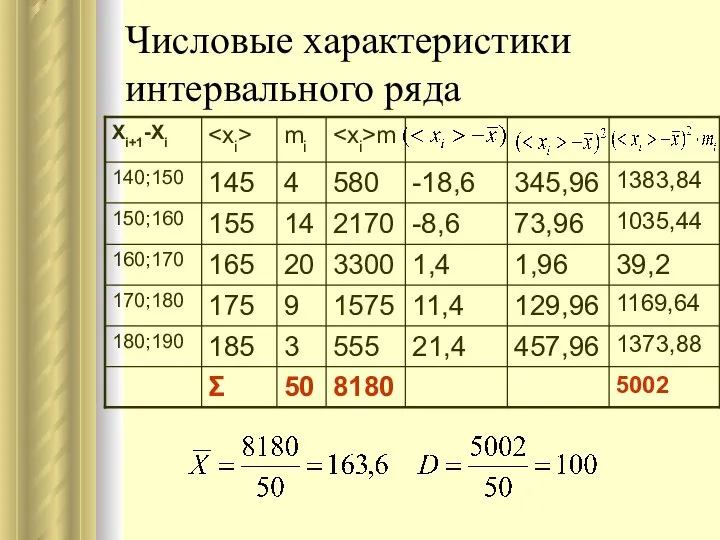
- 41. Числовые характеристики интервального ряда
- 42. поправка Шеппарда При вычислении выборочной дисперсии для уменьшения ошибки, вызванной группировкой (особенно при малом числе интервалов)
- 43. Коэффициенты асимметрии и эксцесса:
- 44. Заключение Нами рассмотрены: Основные понятия выборочного метода; Способы построения дискретных и интервальных вариационных рядов.
- 45. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА: Основная литература: Попов А.М. Теория вероятней и математическая статистика /А.М. Попов, В.Н. Сотников. –
- 47. Скачать презентацию



































 Примеры задач линейного программирования
Примеры задач линейного программирования Рюкзак. Восстановление ответа
Рюкзак. Восстановление ответа Устные упражнения. Выразите в процентах
Устные упражнения. Выразите в процентах Поездка в страну Целых чисел
Поездка в страну Целых чисел Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов
Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов Понятие производной. Решение задачи Коши
Понятие производной. Решение задачи Коши Сравнение дробей с одинаковыми знаменателями
Сравнение дробей с одинаковыми знаменателями Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Теоремы синусов и косинусов (9 класс)
Теоремы синусов и косинусов (9 класс) Степенные ряды
Степенные ряды Презентация на тему Построение диаграмм и графиков функций
Презентация на тему Построение диаграмм и графиков функций  Теория вероятностей. Треугольник Паскаля
Теория вероятностей. Треугольник Паскаля Игра «Математическое кафе»
Игра «Математическое кафе» Программирование линейных алгоритмов
Программирование линейных алгоритмов Теоретическая разминка
Теоретическая разминка Алгоритм решения и успех на ЕГЭ
Алгоритм решения и успех на ЕГЭ Умножение смешанных чисел
Умножение смешанных чисел Умножение на двузначное число. Задачи на построение геометрических фигур
Умножение на двузначное число. Задачи на построение геометрических фигур Числа до 15
Числа до 15 Линейная_Алгебра_1
Линейная_Алгебра_1 Простейшие тригонометрические уравнения, 10 класс
Простейшие тригонометрические уравнения, 10 класс Презентация на тему Площади и объёмы
Презентация на тему Площади и объёмы  Счет 1, 2, 3, 4
Счет 1, 2, 3, 4 Объемы. Соотношения между единицами объема
Объемы. Соотношения между единицами объема Правильные многоугольники в природе
Правильные многоугольники в природе Симметрия вокруг нас
Симметрия вокруг нас Конкретный смысл умножения
Конкретный смысл умножения Повторение: Окружность. Центр окружности. Радиус. Градусная мера дуги окружности
Повторение: Окружность. Центр окружности. Радиус. Градусная мера дуги окружности