Содержание
- 2. Содержание Понятие производной. Алгоритм нахождения производной. Примеры. Таблица производных. Физический смысл производной. Правила нахождения производных. Непрерывность
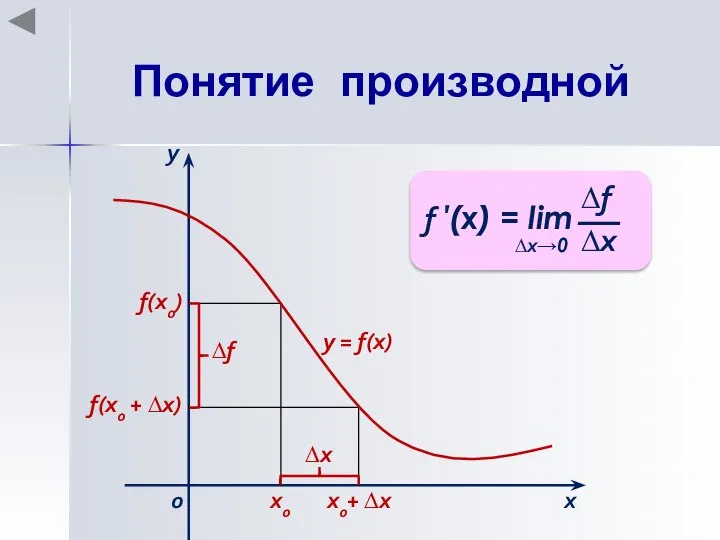
- 3. Понятие производной Производной функции у = f(x), заданной на некотором интервале (a; b), в некоторой точке
- 4. Понятие производной х0 х0+ ∆х f(x0) f(x0 + ∆х) ∆х х у 0 ∆f у =
- 5. Зафиксировать значение х0, найти f(x0). Дать аргументу х0 приращение ∆х, перейти в новую точку х0 +
- 6. Примеры 1. Найти производную функции y = kx + b в точке хo
- 7. Примеры 2. Найти производную функции y = C (C – const) в точке хo
- 8. Примеры 3. Найти производную функции y = x2 в точке хo
- 9. Примеры
- 10. Примеры
- 11. Примеры 5. Найти производную функции y = 1/x в точке хo
- 12. Примеры 5. Найти производную функции y = 1/x в точке хo
- 13. Таблица производных
- 14. Физический ( механический ) смысл производной Если при прямолинейном движении путь s, пройденный точкой, есть функция
- 15. Правила нахождения производной 1. Если функции u(x) и v(x) имеют в точке х производные, то их
- 16. Правила нахождения производной 3. Если функции u(x) и v(x) имеют в точке х производные, то их
- 17. Правила нахождения производной 5. Если функции u(x) и v(x) имеют в точке х производные и v(x)
- 18. Производная сложной функции (f(g(x)))′ = f′(g(x))∙g′(x) Примеры: 1. ((5x – 3)3)′ = 3(5x – 3)2∙(5x –
- 20. Скачать презентацию
















 Сети и потоки
Сети и потоки Математическое моделирование автоматических систем регулирования
Математическое моделирование автоматических систем регулирования Метод координат и метод векторов при решении задач
Метод координат и метод векторов при решении задач Проценты. Обыкновенные и десятичные дроби
Проценты. Обыкновенные и десятичные дроби Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Школа Квентин – подготовка к ЕГЭ
Школа Квентин – подготовка к ЕГЭ Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Треугольник. Геометрия 7 класс. Урок решения задач
Треугольник. Геометрия 7 класс. Урок решения задач Неравенства с одной переменной
Неравенства с одной переменной Ешение систем линейных уравнений методом крамера
Ешение систем линейных уравнений методом крамера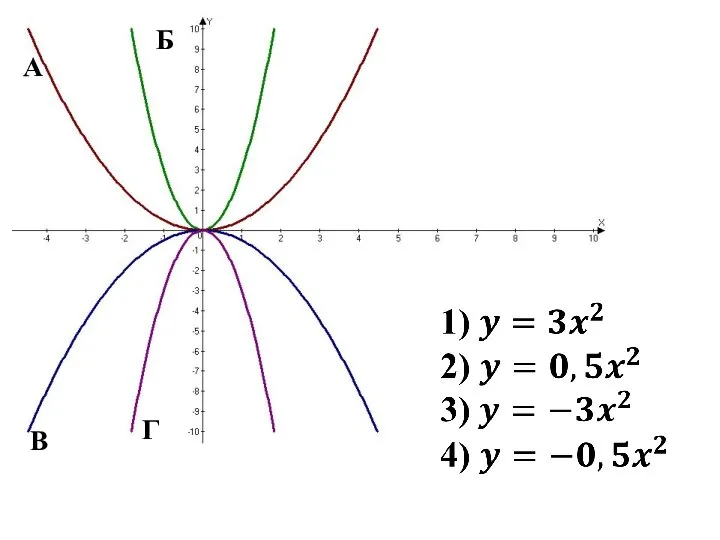 Парабола, гипербола
Парабола, гипербола Великий ученый древнего мира – Архимед и его закон
Великий ученый древнего мира – Архимед и его закон Взаимное расположение Прямых и Плоскостей в пространстве
Взаимное расположение Прямых и Плоскостей в пространстве Математика. Повторение. 1 класс
Математика. Повторение. 1 класс Основы логики. Таблица истинности. Равносильные логические выражения
Основы логики. Таблица истинности. Равносильные логические выражения Понятие, задачи корреляционно-регрессионного анализа и моделирования
Понятие, задачи корреляционно-регрессионного анализа и моделирования Виды треугольников
Виды треугольников Предикати та їх різновиди
Предикати та їх різновиди Из опыта работы учителя математики ГБОУ СОШ с.Курумоч Хохловой Г.В.
Из опыта работы учителя математики ГБОУ СОШ с.Курумоч Хохловой Г.В.  Единицы измерения площадей.
Единицы измерения площадей. МАТЕМАТИКА, 2 КЛАСС программа «Школа России» УМК «Школа России» «ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ» Автор: Рябова И.В. МОУСОШ
МАТЕМАТИКА, 2 КЛАСС программа «Школа России» УМК «Школа России» «ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ» Автор: Рябова И.В. МОУСОШ Задачи на построение
Задачи на построение Методы простых средних и скользящих средних
Методы простых средних и скользящих средних Смежные и вертикальные углы
Смежные и вертикальные углы Национальный стандарт по библиотечной статистике: преемственность и новые подходы
Национальный стандарт по библиотечной статистике: преемственность и новые подходы Таблица умножения и деления на 2
Таблица умножения и деления на 2 Статистика. Основные этапы статистического анализа
Статистика. Основные этапы статистического анализа Перпендикулярные прямые
Перпендикулярные прямые