Содержание
- 2. Слово «логика» происходит от греческого logos, что означает «слово», «разум», «мысль», «закономерность». Логика - наука, которая
- 3. Понятие Понятие - форма мышления, отражающая объекты (предметы или явления) в их существенных и общих свойствах.
- 4. Виды понятий Понятия, которые изучаются в начальном курсе математики, обычно представляют в виде четырех групп. 1)
- 5. Среди свойств объекта различают существенные и несущественные. Свойство считают существенным для объекта, если оно присуще этому
- 6. Объем понятия – это множество всех объектов, которые обобщаются в понятии и обозначаются одним термином. Содержание
- 7. Понятия обозначают строчными буквами латинского алфавита: a, b, c, ..., z. А их объемы соответственно А,
- 8. Отношение рода и вида между понятиями. понятия рода и вида относительны: одно и то же понятие
- 9. Виды определений Явные: - через род и видовое отличие; - генетические; - номинальные. Неявные: - контекстуальные;
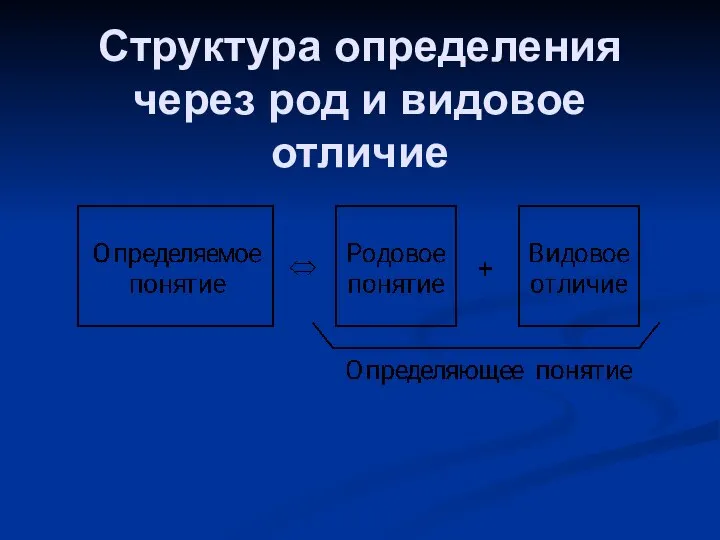
- 10. Структура определения через род и видовое отличие
- 11. Генетические определения видовое отличие указывает способ образования определяемого понятия. Например, симметрией относительно точки называется такое преобразование
- 12. Контекстуальные определения Всякий отрывок текста, всякий контекст, в котором встречается интересующее нас понятие, можно назвать неявным
- 13. Остенсивные определения или определение путем показа. Определить путем показа можно не все понятия, а только простые,
- 14. Аксиоматические определения Совокупность аксиом какой-то теории является одновременно и свернутой формулировкой этой теории, и тем контекстом,
- 15. Правила формулировки определений Определение должно быть соразмерным. В определении (или их системе) не должно быть порочного
- 16. Правила построения нового определения 1. Назвать определяемое понятие (термин). 2. Указать ближайшее родовое (по отношению к
- 17. Высказывание Высказыванием называют предложение, относительно которого имеет смысл вопрос: истинно оно или ложно Высказывания бывают простые
- 18. Истинность и ложность Высказывания принято обозначать A,B,C.. Если А является истинным, то говорят что значение высказывания
- 19. Высказывательная форма О:. Одноместной высказывательной формой, заданной на множестве X, называется предложение с переменной, которое обращается
- 20. Конъюнкция и дизъюнкция Предложение (высказывание или высказывательная форма), построенное с помощью союза «и» из элементарных предложений,
- 21. Кванторы В математике слова «все», «некоторые» и их синонимы называются кванторами. Слово «квантор» латинского происхождения и
- 22. Кванторы общности Слова «любой», «всякий», «все»,«каждый», называются кванторами общности. Обозначается символом ∀ . (∀x ∈ X)
- 23. Квантор существования Слова «существует», «найдется», «для некоторых», «некоторые», «найдется», «существует», «хотя бы один» и др. называются
- 24. Если высказывательная форма содержит несколько переменных, то перевести ее в высказывание можно, если связать квантором каждую
- 25. Установление значения истинности высказываний, содержащих квантор общности Истинность высказывания с квантором общности устанавливается путем доказательства. Показать
- 26. Установление значения истинности высказываний, содержащих квантор существования Истинность высказывания с квантором существования устанавливается при помощи конкретного
- 27. Отрицание высказывания Отрицанием высказывания А называется высказывание , которое ложно, если высказывание A истинно, и истинно,
- 28. Отрицание конъюнкции Чтобы построить отрицание конъюнкции , достаточно заменить отрицаниями составляющие ее высказывания, а союз «и»
- 29. Отрицание дизъюнкции Чтобы построить отрицание дизъюнкции, достаточно заменить отрицаниями составляющие ее высказывания, а союз «или» заменить
- 30. Отрицание высказываний с кванторами Для того, чтобы построить отрицание высказывания, начинающегося с квантора общности (существования), достаточно
- 31. Высказывательная форма B(x) следует из высказывательной формы A(x), если B(x) обращается в истинное высказывание при всех
- 32. Предложение A(x) ⇒ B(x) может быть сформулировано в виде «всякое A(x) есть B(x)». Его истинность устанавливается
- 33. A(x) ⇒ B(x) 1) Из A(x) следует B(x). 2) Всякое A(x) есть B(x). 3) Если A(x),
- 34. Предложения A(x) и B(x) равносильны, если из предложения A(x) следует предложение B(x), а из предложения B(x)
- 35. A(x) ⇔ B(x) предложения равносильны, если они одновременно истинны, либо одновременно ложны, т.е. если их значения
- 36. A(x) ⇔ B(x) 1) A(x) равносильно B(x). 2) A(x) тогда и только тогда, когда B(x). 3)
- 38. Скачать презентацию


































 Справочник по геометрии 7-9 класс
Справочник по геометрии 7-9 класс Понятие алгоритма. Свойства алгоритма. Способы описания алгоритмов: на естественном и алгоритмическом языках, в виде схем
Понятие алгоритма. Свойства алгоритма. Способы описания алгоритмов: на естественном и алгоритмическом языках, в виде схем Решение задач на сложение и вычитание смешанных чисел 5 класс Учебник Дорофеева.
Решение задач на сложение и вычитание смешанных чисел 5 класс Учебник Дорофеева. Математический АУКЦИОН
Математический АУКЦИОН  Элементы линейной алгебры
Элементы линейной алгебры Показательная функция
Показательная функция Теорема о средней линии треугольника
Теорема о средней линии треугольника Презентация по математике "Метод графов" - скачать
Презентация по математике "Метод графов" - скачать  Производная функции
Производная функции Многочлен. Часть 1
Многочлен. Часть 1 Презентация по математике "Таинственная история совершенных чисел" - скачать
Презентация по математике "Таинственная история совершенных чисел" - скачать  Метрология, стандартизация, сертификация
Метрология, стандартизация, сертификация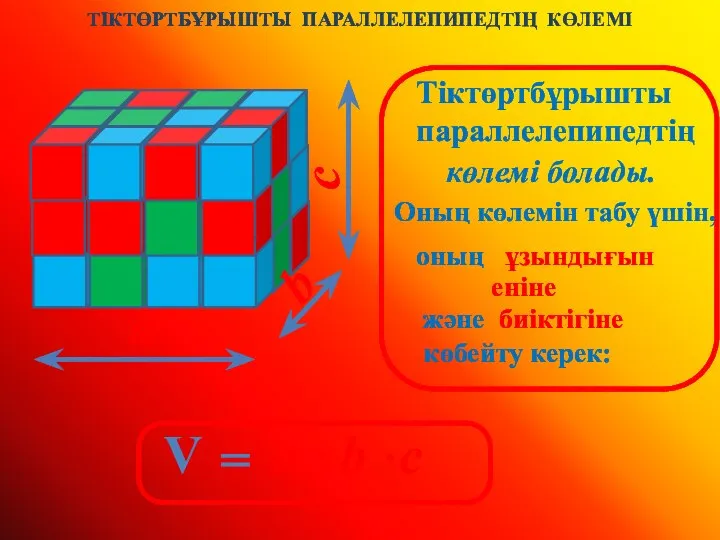 Тіктөртбұрышты параллелепипедтің көлемі
Тіктөртбұрышты параллелепипедтің көлемі Математические формулы
Математические формулы Геометрия (ГИА-9). Задания с выбором ответа
Геометрия (ГИА-9). Задания с выбором ответа Антагонистические игры
Антагонистические игры Презентация по математике "Решение системы линейных уравнений методом Крамера" - скачать бесплатно
Презентация по математике "Решение системы линейных уравнений методом Крамера" - скачать бесплатно Математикадан сыныптан тыс жұмыстар өткізудің әдістемесі; әртүрлі типтегі мектептерде математиканы оқытудың ерекшеліктері
Математикадан сыныптан тыс жұмыстар өткізудің әдістемесі; әртүрлі типтегі мектептерде математиканы оқытудың ерекшеліктері Золотое сечение
Золотое сечение Комбинаторика. 5 класс
Комбинаторика. 5 класс Методы решения нелинейных уравнений. Тема 7
Методы решения нелинейных уравнений. Тема 7 Методика профессионально ориентированного обучения: математика
Методика профессионально ориентированного обучения: математика Урок – игра для 7 класса «Звёздный час»
Урок – игра для 7 класса «Звёздный час» Поле чудес. Геометрия
Поле чудес. Геометрия Практические задачи по математике в 5 классе
Практические задачи по математике в 5 классе Совместные действия с обыкновенными и десятичными дробями
Совместные действия с обыкновенными и десятичными дробями Табличное умножение и деление. Интерактивная игра-презентация по математике
Табличное умножение и деление. Интерактивная игра-презентация по математике С чего начать подготовку к ЕГЭ по профильной математике
С чего начать подготовку к ЕГЭ по профильной математике