Содержание
- 2. Домашнее задание
- 3. Последовательности: определение; примеры. Сходимость последовательностей (вычисление пределов) Что будет на уроке
- 4. Последовательность — это пронумерованный набор каких-либо объектов, среди которых допускаются повторения, причём порядок объектов имеет значение.
- 5. Предмет нашего занятия – числовые последовательности, пронумерованные натуральными числами. В качестве обозначения последовательности обычно используют строчные
- 7. 1 2 3 4 5 6 … n a b c
- 9. Два способа задания числовой последовательности явный неявный
- 10. Явный. В этом случае есть конкретная формула для получения n-го члена последовательности. Эту формулу называют общим
- 11. Неявный. Каждый член последовательности зависит не от номера, а от других элементов последовательности. (но упорядоченность элементов
- 12. Арифметическая и геометрическая прогрессия (последовательность)
- 13. Пример геометрической последовательности
- 14. Пример геометрической последовательности
- 15. Пример геометрической последовательности
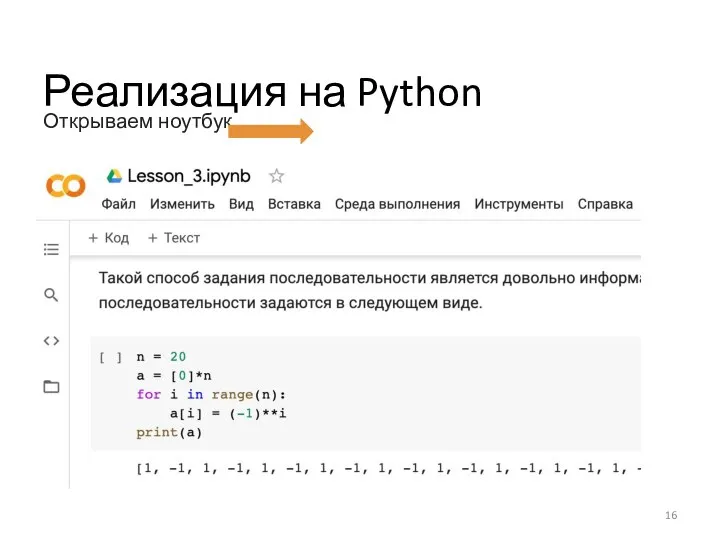
- 16. Реализация на Python Открываем ноутбук
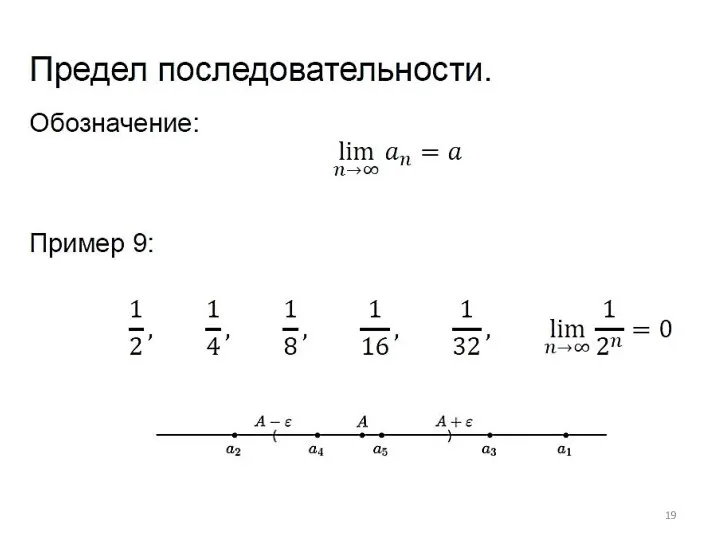
- 17. Сходимость последовательностей (пределы)
- 25. Выяснить тип неопределённости. Если в выражении дробь вида «многочлен делить на многочлен» поделить старшую степень. Поделить
- 27. Какая будет старшая степень?
- 33. Правила вычисления пределов, если в числителе и знаменателе степенные функции если максимальная степень числителя меньше максимальной
- 38. Задача (практическое применение теории пределов) Понять какой из алгоритмов быстрее для сортировки. Есть 3 алгоритма: 1)
- 39. Задача (практическое применение теории пределов) Ход решения – найти пределы частных. Например (решить этот предел можно
- 40. Выводы (правила)
- 45. Сумма членов геометрической прогрессии
- 49. Скачать презентацию












































 Презентация по математике "Умножение и деление десятичных дробей на натуральное число" - скачать
Презентация по математике "Умножение и деление десятичных дробей на натуральное число" - скачать  старинные меры длины
старинные меры длины Сложение и вычитание десятичных дробей. (Урок 110)
Сложение и вычитание десятичных дробей. (Урок 110) Параллельные прямые, перпендикулярные к плоскости
Параллельные прямые, перпендикулярные к плоскости Осевая и центральная симметрия. Тест
Осевая и центральная симметрия. Тест Инструментальная система распределенного имитационного моделирования
Инструментальная система распределенного имитационного моделирования Третий признак равенства треугольников
Третий признак равенства треугольников Потенциальная яма в импульсном представлении
Потенциальная яма в импульсном представлении Функция нескольких переменных
Функция нескольких переменных Подготовка к экзамену по начертательной геометрии
Подготовка к экзамену по начертательной геометрии Сумма углов треугольника
Сумма углов треугольника Измерение углов
Измерение углов Альтернативные методы решения планиметрических задач. Трапеция
Альтернативные методы решения планиметрических задач. Трапеция Задачи на совместную работу (урок открытия новых знаний)
Задачи на совместную работу (урок открытия новых знаний) Измерение отрезков. Блиц-опрос. Геометрия 7 класс
Измерение отрезков. Блиц-опрос. Геометрия 7 класс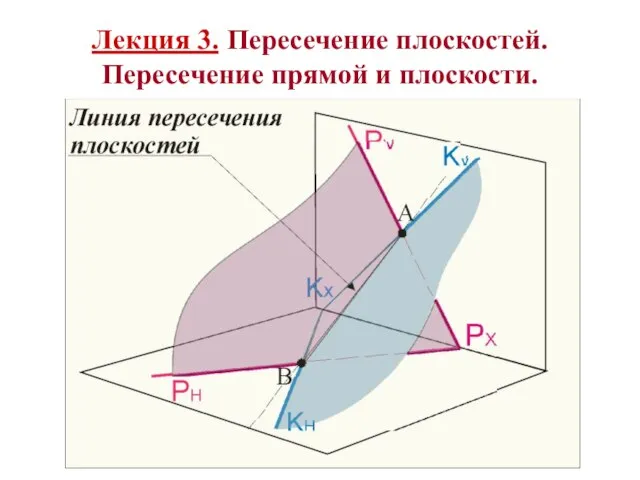 Лекция 3. Пересечение плоскостей. Пересечение прямой и плоскости
Лекция 3. Пересечение плоскостей. Пересечение прямой и плоскости Проценты. Три задачи
Проценты. Три задачи Displaying data – shape of distributions. Week 3 (1)
Displaying data – shape of distributions. Week 3 (1) Степенные функции и их графики
Степенные функции и их графики Занимательная математика
Занимательная математика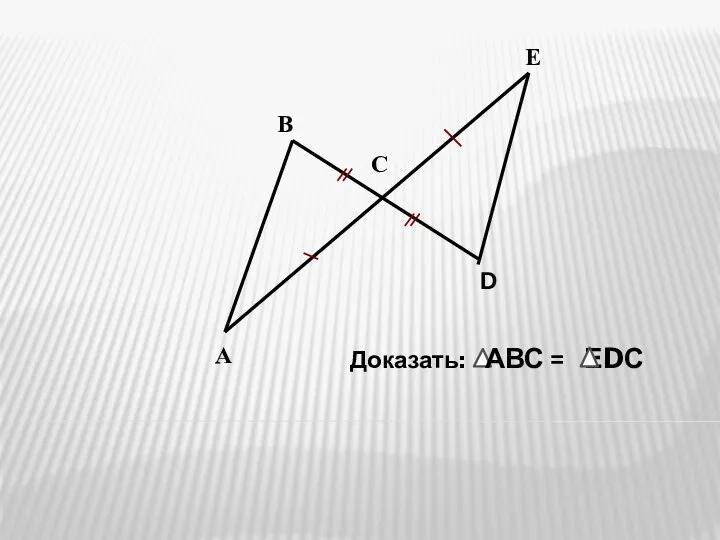 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Развивающие игры Воскобовича. Геоконт
Развивающие игры Воскобовича. Геоконт Уравнения с одной переменной. Цель :выявить связь между теорией и практикой при решении уравнений с одной переменной. Задачи: -пр
Уравнения с одной переменной. Цель :выявить связь между теорией и практикой при решении уравнений с одной переменной. Задачи: -пр Створення системи розвивальних завдань у навчанні математики учнів 5 – 6 класів
Створення системи розвивальних завдань у навчанні математики учнів 5 – 6 класів Сумма углов треугольника
Сумма углов треугольника Задачи на нахождение четвертого пропорционального. Урок математики (4 класс)
Задачи на нахождение четвертого пропорционального. Урок математики (4 класс) Призма, рiзновид – паралелепiпед
Призма, рiзновид – паралелепiпед Введение в начертательную геометрию. Теория параметризации. (Лекция 1)
Введение в начертательную геометрию. Теория параметризации. (Лекция 1)