- Главная
- Математика
- Последовательности. Предел последовательности. (Семинар 1)

Содержание
- 2. Теорема 4 Разность сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен разности пределов последовательностей и
- 3. 2.Ограниченные и неограниченные последовательности Определение 1. Последовательность называется ограниченной сверху (снизу), если существует такое число M
- 4. 2)Последовательность 1, ½,1/3,…,1/n, … - ограничена. 3)Последовательность 1, 2, 1, 3, ….,n, 1, (n+1), … -
- 5. произвольное число . Неравенство будет выполнено, если то есть при . В качестве N возьмем какое-нибудь
- 6. Учитывая, что - бесконечно малые последовательности, и используя теоремы о пределах, получаем Пример 5. Пусть для
- 7. Поскольку Задания для самостоятельного решения Доказать, что , указав для каждого такое N, что для любого
- 9. Скачать презентацию
Теорема 4
Разность сходящихся последовательностей и есть сходящаяся последовательность, предел
Теорема 4
Разность сходящихся последовательностей и есть сходящаяся последовательность, предел
Теорема 5
Произведение сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей и .
Теорема 6
Частное двух сходящихся последовательностей и при условии, что предел последовательности отличен от 0, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей и .
Теорема 7
Если элементы сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравенству , то и предел а этой последовательности удовлетворяет неравенству
Теорема 8
Пусть и . Пусть также начиная с некоторого номера элементы последовательности удовлетворяют неравенству
, тогда
2.Ограниченные и неограниченные последовательности
Определение 1. Последовательность называется ограниченной сверху (снизу), если
2.Ограниченные и неограниченные последовательности
Определение 1. Последовательность называется ограниченной сверху (снизу), если
M – верхняя грань; m – нижняя грань. - условие ограниченности последовательности сверху (снизу).
Замечание Любая ограниченная сверху (снизу) последовательность имеет бесчисленное множество верхних ( нижних) граней.
Определение 2. Последовательность называется ограниченной с обеих сторон или просто ограниченной, если существует такие числа M и m, что каждый элемент последовательности удовлетворяет неравенству
M – верхняя грань; m – нижняя грань.
Если ограничена, то все элементы этой последовательности удовлетворяют неравенству , где
Определение 3. Последовательность называется неограниченной, если для любого положительного числа А найдется элемент этой последовательности, удовлетворяющий неравенству .
Примеры:
1)последовательность -1, -4, -9, …,- ,… - ограничена сверху и не ограничена снизу. Верхняя грань – число больше или равно -1.
2)Последовательность 1, ½,1/3,…,1/n, … - ограничена.
3)Последовательность 1, 2,
2)Последовательность 1, ½,1/3,…,1/n, … - ограничена.
3)Последовательность 1, 2,
3. Монотонные последовательности
Определение
Последовательность называется неубывающей (невозрастающей), если для всех номеров n справедливо неравенство
Общее название – монотонные последовательности.
Если для всех n - возрастающая.
Если для всех n - убывающая.
Общее название – строго монотонные.
4. Бесконечно большие и бесконечно малые последовательности
Определение 1.
Последовательность называется бесконечно большой, если для любого положительного числа А можно указать номер N такой, что для все элементы удовлетворяют неравенству
Определение 2
Последовательность называется бесконечно малой, если для , можно указать номер N такой, что при все элементы этой последовательности удовлетворяют неравенству .
Примеры с решениями
Пример 1. Доказать исходя из определения, что число 1 является пределом последовательности
Доказательство. Рассмотрим модуль разности . Введем
произвольное число . Неравенство будет выполнено, если то есть при
произвольное число . Неравенство будет выполнено, если то есть при
выполнены неравенства . Это и означает, что число 1
есть предел последовательности , то есть
Пример 2. Доказать исходя из определения, что .
Доказательство.
Так как для любого , то .
Пусть , выберем натуральное N такое, что . Тогда для любого имеем . Значит .
Пример 3. Доказать, что последовательность расходится.
Доказательство. Докажем, что данная последовательность неограниченна. Имеем
Пусть С – произвольное положительное число. Возьмем какое-нибудь натуральное число , тогда . Это означает, что последовательность
Пример 4. Найти
Решение. Преобразуем формулу общего элемента к виду
неограниченна, а поэтому расходится.
.
Учитывая, что - бесконечно малые последовательности, и используя теоремы о
Учитывая, что - бесконечно малые последовательности, и используя теоремы о
Пример 5. Пусть для любого n; пусть p – натуральное число.
Доказать, что
Доказательство. Если ,
а если поэтому .
Объединяя эти результаты, для любого получаем .
Так как и . Отсюда
следует, что и
Пример 6. Найти
Решение. Преобразуем формулу общего элемента:
.
Поскольку
Задания для самостоятельного решения
Доказать, что
, указав для каждого
такое
Поскольку
Задания для самостоятельного решения
Доказать, что
, указав для каждого
такое
верно неравенство
, если
1)
2)
(a – произвольное данное число);
4)
5)
6)
3)
2. Доказать, что:
2)
3)
4)
5)
6)
1)
Доказать, что
- бесконечно малая последовательность, если






 Дифференциальные уравнения. (Лекция 3)
Дифференциальные уравнения. (Лекция 3) Поиск оптимального пути в 3D
Поиск оптимального пути в 3D Расстояние от точки до плоскости. Теорема о трех перпендикулярах
Расстояние от точки до плоскости. Теорема о трех перпендикулярах Проект по математике. Фигуры на координатной плоскости
Проект по математике. Фигуры на координатной плоскости Математический диктант. 4 класс
Математический диктант. 4 класс Обыкновенные дроби. Задания для устного счета. 8 класс
Обыкновенные дроби. Задания для устного счета. 8 класс Теорема Пифагора
Теорема Пифагора Математическое путешествие по сказке (для дошкольников)
Математическое путешествие по сказке (для дошкольников) Презентация по математике "Урок одного уравнения" - скачать бесплатно
Презентация по математике "Урок одного уравнения" - скачать бесплатно Сложение чисел с разными знаками
Сложение чисел с разными знаками Формы выражения статистических показателей
Формы выражения статистических показателей Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель
Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель  Обратные действия
Обратные действия Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Иллюзии в математике
Иллюзии в математике Предикаты и кванторы. Действия над предикатами и их свойства
Предикаты и кванторы. Действия над предикатами и их свойства Решение логарифмических уравнений и неравенств
Решение логарифмических уравнений и неравенств Introductory statistics
Introductory statistics Угол поворота. Радианная мера угла
Угол поворота. Радианная мера угла Тригонометрические уравнения
Тригонометрические уравнения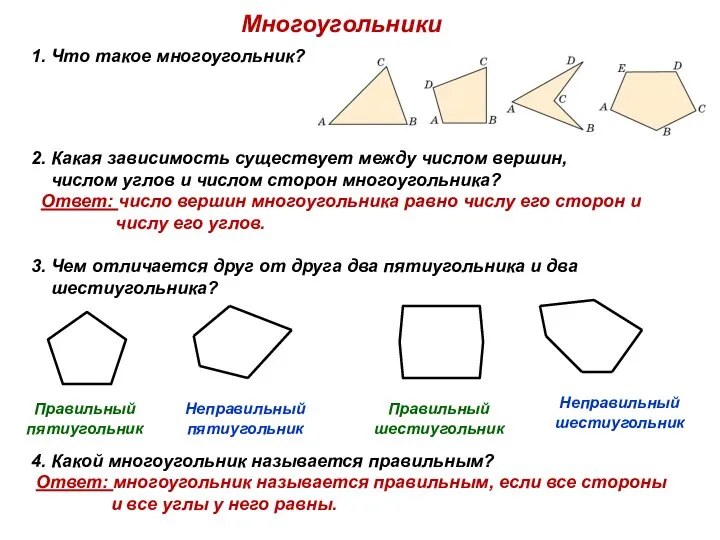 Многоугольники
Многоугольники Моделирование систем
Моделирование систем Четырехугольники. Определение
Четырехугольники. Определение Многозначные числа
Многозначные числа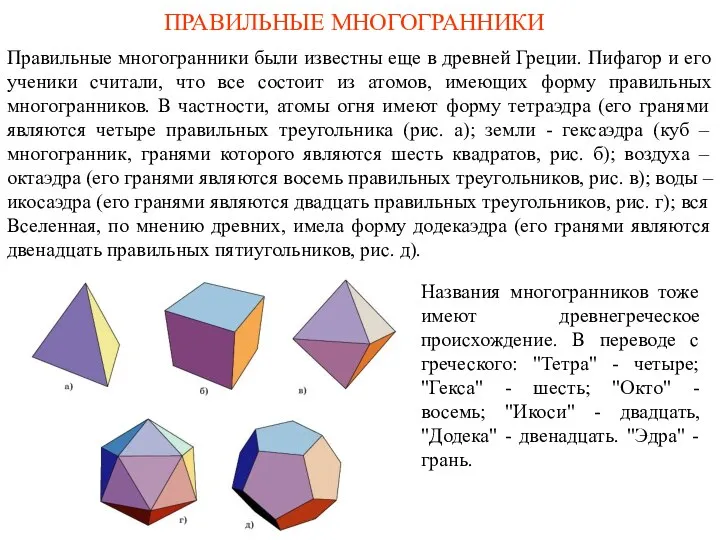 Правильные многогранники
Правильные многогранники Счет 1, 2, 3, 4
Счет 1, 2, 3, 4 Методы многопарметрической оптимизации
Методы многопарметрической оптимизации Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний
Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний