Содержание
- 2. Бесконечно малая и бесконечно большие величины. Переменная величина α называется бесконечно малой, если она изменяется так,
- 3. Переменная величина у называется бесконечно большой, если она изменяется так, что какое бы большое положительное число
- 4. Связь между бесконечно малой и бесконечно большой величины. 1) если , то 2) если , то
- 5. пример: 1) , тогда 2) , тогда
- 6. Предел переменной Число 3 называется пределом переменной х: или
- 7. Постоянная а называется пределом переменной х, если разность между ними есть бесконечно малая величина α�, т.е
- 8. Предел функции
- 9. Определение «на языке последовательности» Число а называется пределом функции f(x) в точке х=х0, если для всех
- 10. Односторонние пределы. Пределы функций при х→х0- и х→х0+ Определение «на языке последовательности»: если f(x) стремится к
- 11. Определение «на языке последовательности»: если f(x) стремится к пределу а при х→х0 так, что х принимает
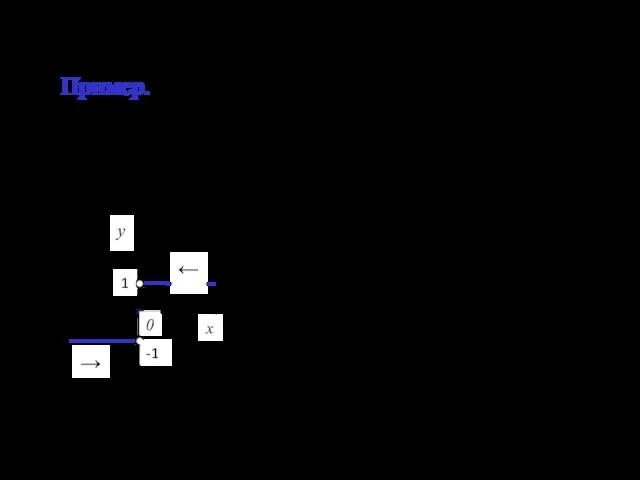
- 12. Пример. у х 0 ← → 1 -1
- 13. Связь между односторонними пределами. Теорема. Функция f(x) имеет в точке х0 предел а тогда и только
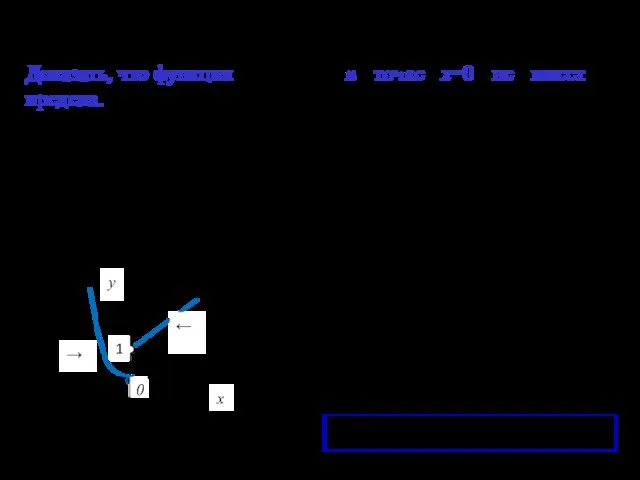
- 14. Доказать, что функция в точке х=0 не имеет предела. не существует у x 0 ← →
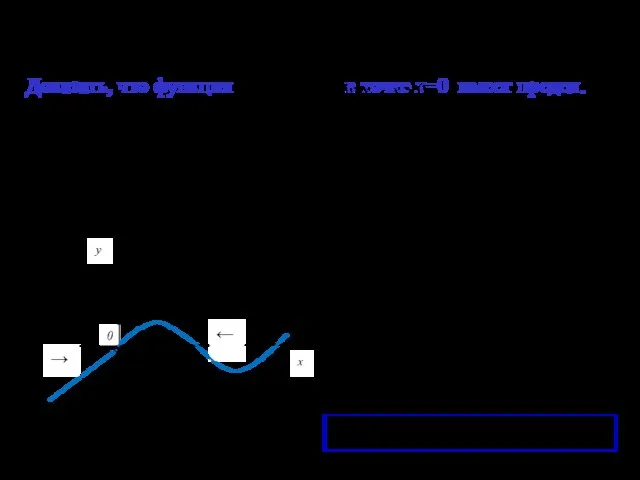
- 15. Доказать, что функция в точке х=0 имеет предел. существует y x 0 ← →
- 16. Пределы функций при х→∞, х→ - ∞ и х→+∞ Определение «на языке последовательности»: число а называется
- 17. Определение «на языке последовательности»: число а называется пределом функции f(x) при х→+∞ (х→-∞), если для всех
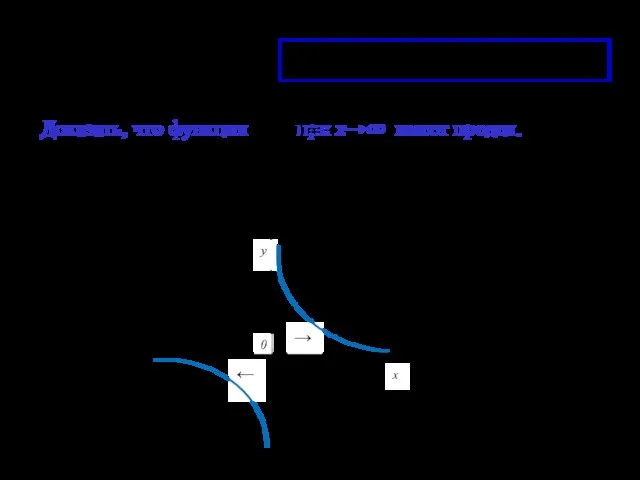
- 18. Справедлива теорема Доказать, что функция при х→∞ имеет предел. существует у x 0 ← →
- 19. Бесконечно малые и бесконечно большие функции. Функция α=α(х) называется бесконечно малой функцией (или просто бесконечно малой)
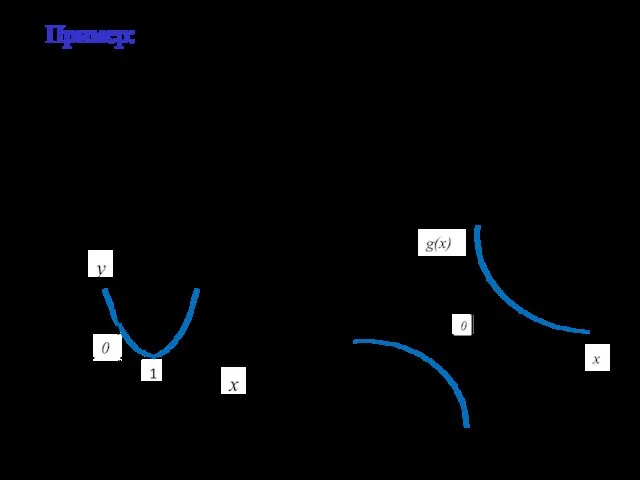
- 20. Пример: 1) функция есть бесконечно малая при х→1, т.к 2) функция есть бесконечно малая при х→∞,
- 21. Функция f(x) называется бесконечно большой функцией (или просто бесконечно большой) в точке х=х0 (или при х→х0),
- 22. Замечание. Функция y=f(x) при х→х0 или при х→∞ может не стремиться к конечному пределу или к
- 23. Основные теоремы о пределах
- 24. Основные теоремы о пределах 7) Пусть функции f(x), g(x) и h(x) определены в некоторой окрестности точки
- 25. I.Вычисление пределов функций. 1) Вычислить
- 26. 2) Вычислить убедимся, что предел знаменателя отличен от 0: тогда применима теорема о пределе дроби:
- 27. II. Вычисление пределов функций. Предел знаменателя равен 0. 3) Вычислить ⇒ (3х-12) есть бесконечно малая величина,
- 28. 4) Вычислить неопределённость
- 29. 5) Вычислить
- 30. III. Вычисление пределов функций. Предел функции при х→∞. 6) Вычислить (4х+3) при х→∞ есть бесконечно большая
- 31. 7) Вычислить
- 33. Скачать презентацию























 Параллельные прямые
Параллельные прямые Корень n – ой степени
Корень n – ой степени Урок математики в 3 классе
Урок математики в 3 классе Решение алгебраических уравнений Выполнил: Нелюбин Алексей 9 «В» класс Школа№3 г. Свирск
Решение алгебраических уравнений Выполнил: Нелюбин Алексей 9 «В» класс Школа№3 г. Свирск  Неравенства. Тест
Неравенства. Тест Системы исчисления у разных племен и народов
Системы исчисления у разных племен и народов Умножение одночлена на многочлен
Умножение одночлена на многочлен Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Умножение 2 и на 2
Умножение 2 и на 2 Ряды. Числовые ряды
Ряды. Числовые ряды Презентация по математике "Определение синуса, косинуса, тангеса острого угла прямоугольного треугольника" - скачать
Презентация по математике "Определение синуса, косинуса, тангеса острого угла прямоугольного треугольника" - скачать  Предмет и задачи начального обучения математике в школе для детей с ТНР
Предмет и задачи начального обучения математике в школе для детей с ТНР Движение в геометрии
Движение в геометрии Презентация по математике "Рациональные числа" - скачать бесплатно
Презентация по математике "Рациональные числа" - скачать бесплатно Міри маси, часу, довжини
Міри маси, часу, довжини Произведение двух последовательных отрицательных чисел
Произведение двух последовательных отрицательных чисел Свойства логарифмов
Свойства логарифмов Математическое ожидание случайной величины
Математическое ожидание случайной величины Урок математики в 1 классе. Прибавить и вычесть число 3. Решение текстовых задач
Урок математики в 1 классе. Прибавить и вычесть число 3. Решение текстовых задач Старинные задачи по элементарной математике
Старинные задачи по элементарной математике Сравнительная оценка методов построения отказоустойчивых и высоконадежных управляющих систем безопасности и аварийной защиты
Сравнительная оценка методов построения отказоустойчивых и высоконадежных управляющих систем безопасности и аварийной защиты Движение
Движение Состав числа 10
Состав числа 10 Квадратный корень из дроби
Квадратный корень из дроби Подобные треугольники. 8 класс
Подобные треугольники. 8 класс Нахождение части целого и целого по его части
Нахождение части целого и целого по его части Векторы в пространстве
Векторы в пространстве Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел