Презентация по математике "Дифференциальное исчисление функции одной переменной" - скачать бесплатно
Содержание
- 2. Дифференциальное исчисление функции одной переменной.
- 3. Определение производной Производной функции y=f(x) в точке х0 Называется , если этот предел существует. Производная обозначается
- 4. Таблица производных
- 7. Правила Дифференцирования Пусть u=u(x) и v=v(x) – функции, дифференцируемые в точке х. Тогда в этой точке
- 8. Производная сложной функции Пусть y=f(u), а u=φ(x). Тогда функция y=f(φ(x)) называется сложной функцией от х. Теорема.
- 9. 16.
- 10. Дифференцирование функций, заданных параметрически Пусть функция y от х задана параметрически уравнениями: x=x(t), y=y(t), t (α;β).
- 11. Пример x=cos3t, y=sin3t. Вычислить yx´´. поэтому
- 12. Дифференцирование функций, заданных неявно. Вычислить y´x, если y5+xy-x2=0. Продифференцируем обе части по х. Получим 5y4y´+y+xy´-2x=0, откуда
- 13. Логарифмическое дифференцирование Найти производную функции y=(sinx)x. Логарифмируем функцию по основанию е: lny=x.lnsinx. Дифференцируем обе части равенства
- 14. Дифференциал функции dy=f´(x)∙dx
- 15. Некоторые теоремы о дифференцируемых функциях!
- 16. Теорема Ферма Пусть функция y=f(x) определена в интервале (a;b) и принимает в точке с этого интервала
- 17. Теорема Ролля Пусть функция y=f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b) и f(a)=f(b)=0. Тогда
- 18. Теорема Лагранжа Пусть функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b). Тогда существует
- 19. Теорема Лопиталя (правило Лопиталя). Пусть f(x) и φ(x) – функции, непрерывные на [a;b], дифференцируемые на (a;b);
- 20. Пример
- 21. Применение производной к исследованию функций
- 22. Экстремумы функции.
- 23. Необходимо условие монотонности функции Если дифференцируемая в интервале (a;b) функция y=f(x) возрастает (убывает) на (a;b), то
- 24. Достаточный признак существования экстремума Если непрерывная на интервале функция y=f(x) имеет производную f´(x) во всех точках
- 25. Выпуклость и вогнутость графика функции График дифференцируемой функции называется выпуклым (вогнутым) в интервале (a;b), если он
- 26. Достаточный признак выпуклости и вогнутости Пусть функция y=f(x) имеет вторую производную f´(x) во всех точках интервала
- 27. Достаточный признак существования точки перегиба Если вторая производная f´(x) непрерывной функции меняет знак при переходе аргумента
- 28. Асимптоты графика функции Асимптотой графика функции y=f(x) называется прямая, расстояние от которой до текущей точки графика
- 29. План исследования функции и построение графика Область определения функции. Точки пересечения графика функции с осями координат.
- 30. Пример Исследовать функцию и построить ее график. Область определения: так как при х=-2 и х=2 знаменатель
- 31. 2. Пусть х=0, тогда у=0. Пусть у=0, тогда , откуда х=0. (0;0) – точка пересечения графика
- 32. - функция четная.
- 33. 4. Функция имеет разрывы в точках х=-2 и х=2, так как f(-2) и f(2) не определены.
- 34. 5.Невертикальные асимптоты следовательно, прямая у=1 – асимптота.
- 35. 6. у´=0, если -8х=0, откуда х=0 – критическая точка. Откуда х=-2 и х=2 – критические точки.
- 36. 7. у´´≠0 при х(-∞;∞), х=-2 и х=2 – критические точки второго порядка. На интервалах (-∞;-2) и
- 38. Скачать презентацию















![Теорема Ролля Пусть функция y=f(x) непрерывна на отрезке [a;b], дифференцируема на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1257351/slide-16.jpg)
![Теорема Лагранжа Пусть функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1257351/slide-17.jpg)













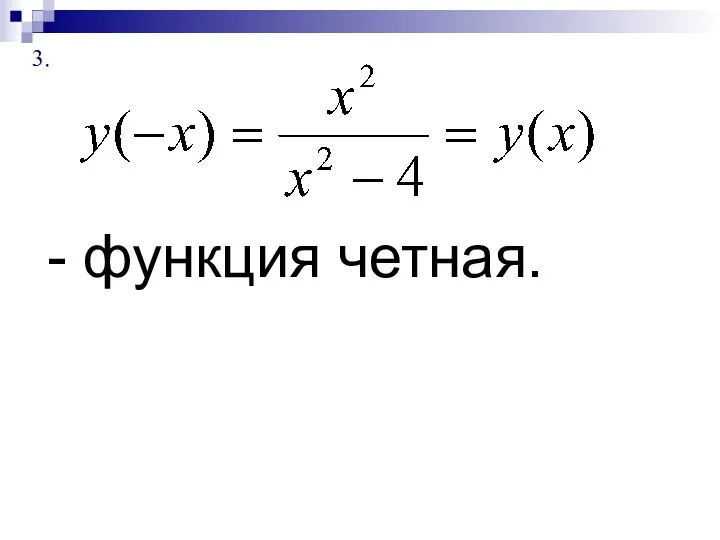




 Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Аттестационная работа. Организация проектной деятельности на уроках математики в основной школе
Аттестационная работа. Организация проектной деятельности на уроках математики в основной школе Булева алгебра
Булева алгебра Алгебра. Подготовка к контрольной работе
Алгебра. Подготовка к контрольной работе Дисперсионный анализ
Дисперсионный анализ Задачи на чертежах по теме трапеция
Задачи на чертежах по теме трапеция Аттестационная работа. Проектно – исследовательская деятельность на уроках математики
Аттестационная работа. Проектно – исследовательская деятельность на уроках математики Точка, линия, прямая и кривая линии. Число 2. Цифра 2
Точка, линия, прямая и кривая линии. Число 2. Цифра 2 Презентация по математике "Игра по математике: Считаем со Смешариками!" - скачать
Презентация по математике "Игра по математике: Считаем со Смешариками!" - скачать  Аттестационная работа. Курс дополнительного образования «Математическая эстафета»
Аттестационная работа. Курс дополнительного образования «Математическая эстафета» Область определения функции. Урок индивидуального обучения
Область определения функции. Урок индивидуального обучения Численные методы решения нелинейных уравнений и систем нелинейных уравнений
Численные методы решения нелинейных уравнений и систем нелинейных уравнений Презентация на тему Нахождение наибольшего и наименьшего значения функции
Презентация на тему Нахождение наибольшего и наименьшего значения функции  Геометрические характеристики плоских сечений
Геометрические характеристики плоских сечений Приёмы письменного деления на однозначное число
Приёмы письменного деления на однозначное число Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал
Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал Решение задач. Определение по графикам формулы функций
Решение задач. Определение по графикам формулы функций Определения многогранников. Теорема Эйлера
Определения многогранников. Теорема Эйлера Деление многозначного числа на однозначное
Деление многозначного числа на однозначное Кривые на плоскости
Кривые на плоскости Подготовка к ГИА. Решение задач обязательной части ГИА по геометрии. Задачи № 9, 10
Подготовка к ГИА. Решение задач обязательной части ГИА по геометрии. Задачи № 9, 10 Правильные многогранники
Правильные многогранники Степенева функція
Степенева функція Дидактическая игра как средство повышения эффективности урока математики
Дидактическая игра как средство повышения эффективности урока математики Геометрическая подготовка младшего школьника
Геометрическая подготовка младшего школьника Площадь трапеции. Свойства площадей
Площадь трапеции. Свойства площадей Десятичные дроби и метрическая система мер
Десятичные дроби и метрическая система мер Сравнение дробей. 5 класс
Сравнение дробей. 5 класс