Презентация по математике "Полная и неполная индукция. Метод математической индукции" - скачать бесплатно
Содержание
- 2. Дедуктивный и индуктивный метод В основе всякого математического исследования лежат дедуктивный и индуктивный методы. Дедуктивный метод
- 3. Полная и неполная индукция Метод математической индукции можно сравнить с прогрессом. Мы начинаем с низшего, в
- 4. Полная индукция Пусть требуется установить, что каждое натуральное чётное число n в пределах 4≤n≤20 представимо в
- 5. Неполная индукция Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных
- 6. Метод математической индукции Пусть нужно доказать справедливость некоторого утверждения для любого натурального числа n. Непосредственная проверка
- 7. Ханойские башни Есть три стержня и колец разного размера. Класть можно только кольцо меньшего размера на
- 8. Пересечение прямых Докажите, что любые n прямых, расположенных на одной плоскости, никакие две из которых не
- 9. Докажите тождество 1. [БАЗА]Проверим, работает ли эта формула при n=1: 2.[ПРЕДПОЛОЖЕНИЕ] Предположим, что тождество верно при
- 11. Рефлексия
- 13. Скачать презентацию







![Докажите тождество 1. [БАЗА]Проверим, работает ли эта формула при n=1: 2.[ПРЕДПОЛОЖЕНИЕ]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1267694/slide-8.jpg)


 Физический и механический смысл производных. Использование производной в физике, механике
Физический и механический смысл производных. Использование производной в физике, механике Производная и первообразная
Производная и первообразная Презентация по математике "Измерение отрезков" - скачать бесплатно
Презентация по математике "Измерение отрезков" - скачать бесплатно Презентация по математике "ДЕСЯТОК. ДВУЗНАЧНЫЕ ЧИСЛА (1 КЛАСС)" - скачать бесплатно
Презентация по математике "ДЕСЯТОК. ДВУЗНАЧНЫЕ ЧИСЛА (1 КЛАСС)" - скачать бесплатно Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Функции y = tg x, y = ctg x, их свойства и графики
Функции y = tg x, y = ctg x, их свойства и графики Цилиндры в профессии повар, кондитер
Цилиндры в профессии повар, кондитер Урок математики в 1 классе На тему : Число 0. Составила ЛАПШИНА ГАЛИНА МАТВЕЕВНА, учитель начальных классов МО
Урок математики в 1 классе На тему : Число 0. Составила ЛАПШИНА ГАЛИНА МАТВЕЕВНА, учитель начальных классов МО Методы решения нелинейных уравнений. Тема 7
Методы решения нелинейных уравнений. Тема 7 Неопределенный интеграл
Неопределенный интеграл Основные тригонометрические формулы
Основные тригонометрические формулы Деление обыкновенных дробей. 6 класс
Деление обыкновенных дробей. 6 класс Многогранники в нашей жизни
Многогранники в нашей жизни Презентация по математике "Построение графиков функций сложных функций на основе свойств монотонности" - скачать
Презентация по математике "Построение графиков функций сложных функций на основе свойств монотонности" - скачать  Показательная и логарифмическая функции. Показательные уравнения
Показательная и логарифмическая функции. Показательные уравнения Математические методы в инженерии
Математические методы в инженерии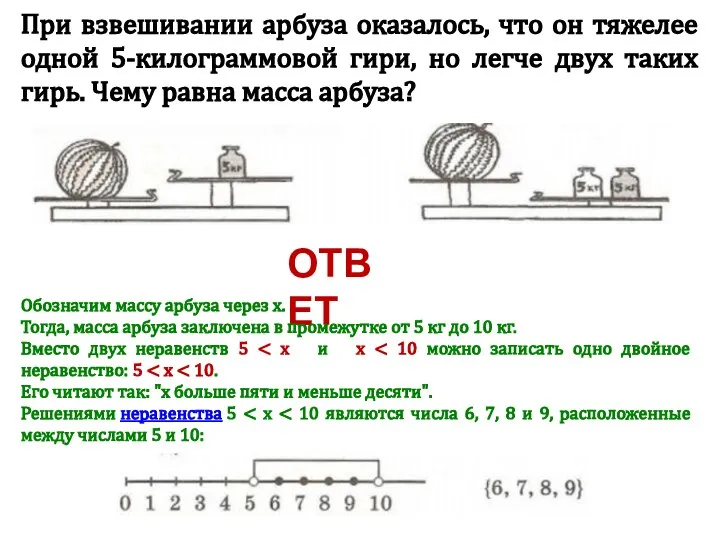 Двойное неравенство
Двойное неравенство Формулы. Урок 1
Формулы. Урок 1 Умножение многочлена на многочлен
Умножение многочлена на многочлен Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии Признаки равенства треугольников
Признаки равенства треугольников Анализ геометрической формы. Порядок чтения чертежей деталей
Анализ геометрической формы. Порядок чтения чертежей деталей Логарифмическая производная. Производная функции, заданной параметрическими уравнениями. (Семинар 9)
Логарифмическая производная. Производная функции, заданной параметрическими уравнениями. (Семинар 9) Изучение научных методов обработки экспериментальных данных
Изучение научных методов обработки экспериментальных данных Упражнения
Упражнения Обернена функція
Обернена функція Алгоритм решения неравенств методом интервалов
Алгоритм решения неравенств методом интервалов Тренировочный тест. Значение выражений
Тренировочный тест. Значение выражений