Содержание
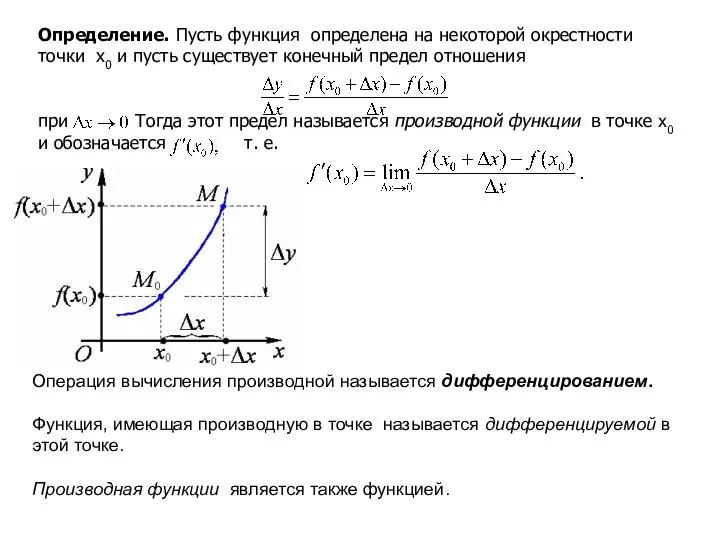
- 2. Определение. Пусть функция определена на некоторой окрестности точки x0 и пусть существует конечный предел отношения при
- 3. Дифференцируемость – более сильное условие на функцию, чем непрерывность. Теорема. Всякая функция, дифференцируемая в точке непрерывна
- 9. Применение производной в экономике Пусть у(х) — затраты на изготовление х экземпляров некоторого продукта. Тогда у'(х)
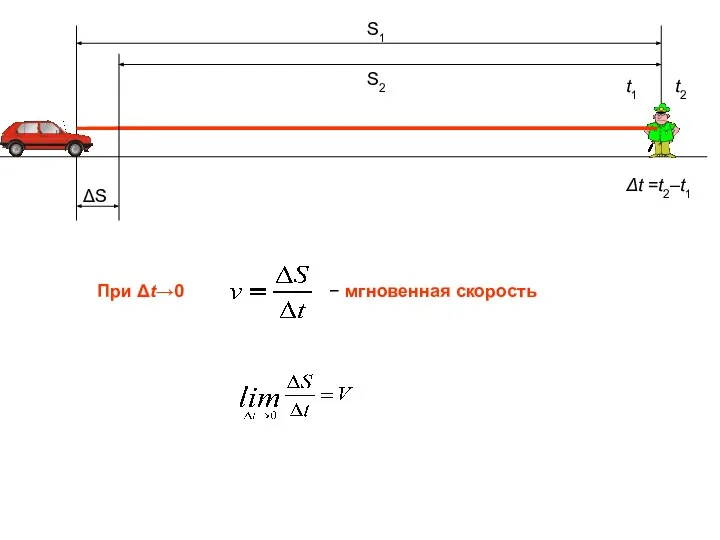
- 10. Физический смысл производной Физический смысл производной. Производная характеризует скорость изменения одной физической величины по отношению к
- 11. t1 t2 Δt =t2–t1 S1 S2 При Δt→0 − мгновенная скорость
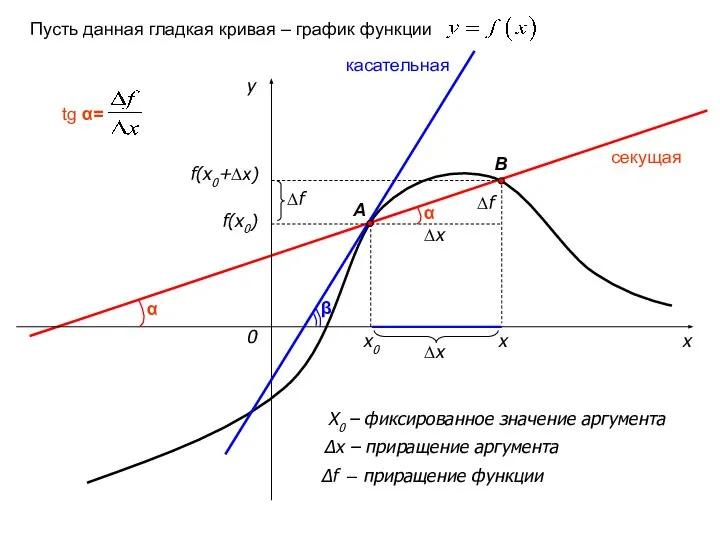
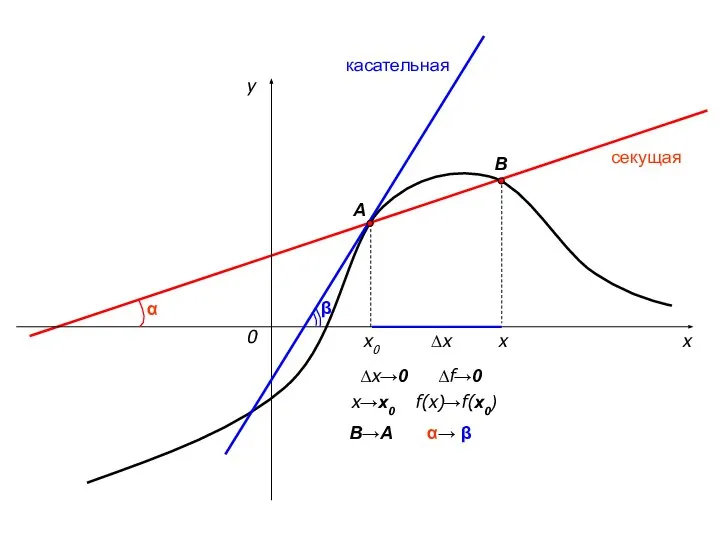
- 12. x y 0 x0 x ∆x секущая касательная Пусть данная гладкая кривая – график функции A
- 13. x y 0 x0 x ∆x ∆x→0 x→x0 секущая касательная A B B→A β ∆f→0 α→
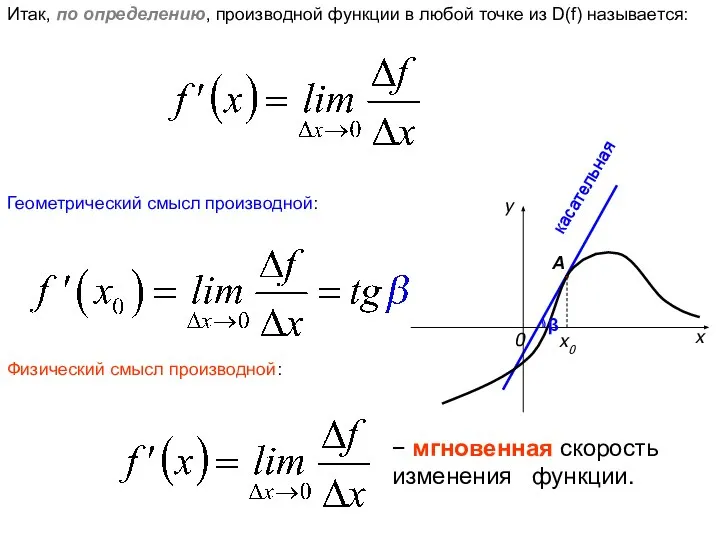
- 14. Итак, по определению, производной функции в любой точке из D(f) называется: Геометрический смысл производной: Физический смысл
- 16. Скачать презентацию



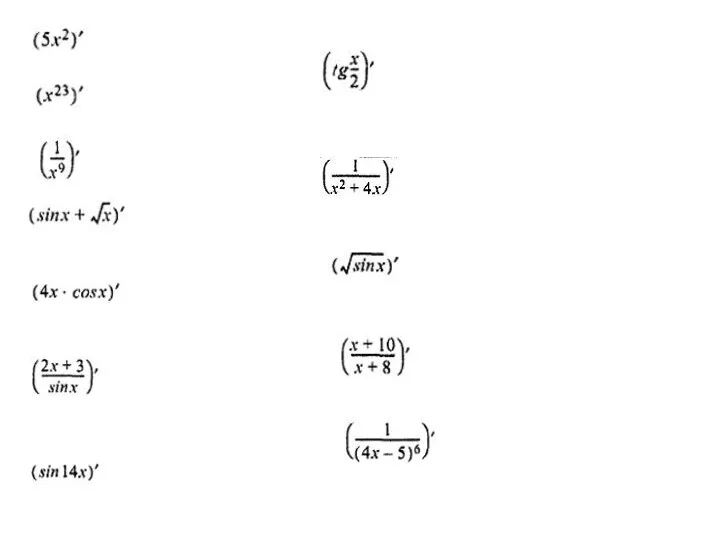




 Деление дробей. 6 класс
Деление дробей. 6 класс Презентация по математике "Построение пирамиды в зависимости от положения высоты" - скачать
Презентация по математике "Построение пирамиды в зависимости от положения высоты" - скачать  Пифагоровы тройки чисел
Пифагоровы тройки чисел Вычисление криволинейных интегралов 2 рода
Вычисление криволинейных интегралов 2 рода Признаки делимости
Признаки делимости Умножение рациональных чисел
Умножение рациональных чисел Решение логарифмических неравенств с помощью метода рационализации
Решение логарифмических неравенств с помощью метода рационализации Признаки равенства треугольников
Признаки равенства треугольников Решение задач с помощью уравнений (6 класс)
Решение задач с помощью уравнений (6 класс)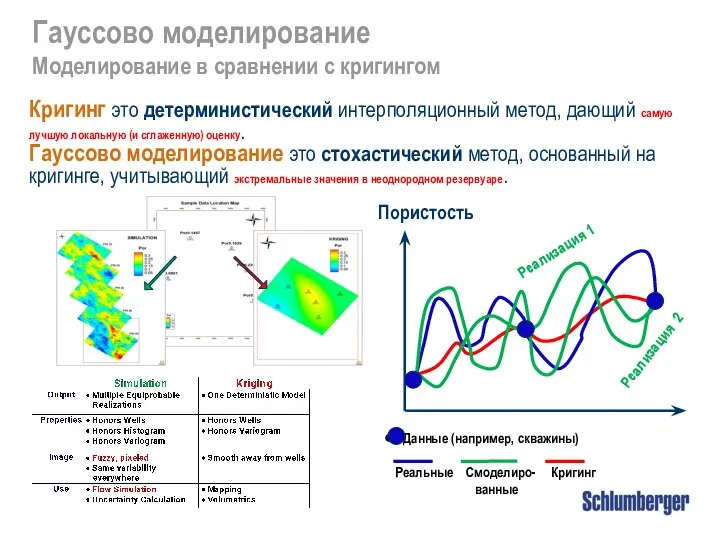 Гауссово моделирование
Гауссово моделирование Элективный курс по математике для учащихся 9 классов
Элективный курс по математике для учащихся 9 классов Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Геометрические фигуры и их свойства. Электронный справочник
Геометрические фигуры и их свойства. Электронный справочник Конформные отображения
Конформные отображения Линейные ДУ
Линейные ДУ Линейное уравнение с одной переменной. Решение задач. 8 класс
Линейное уравнение с одной переменной. Решение задач. 8 класс Презентация по математике "Числа 1-5" - скачать
Презентация по математике "Числа 1-5" - скачать  Лекция 9. Понятие о конечных автоматах
Лекция 9. Понятие о конечных автоматах Сфера, описанная вокруг многогранника
Сфера, описанная вокруг многогранника Презентация по математике "Решение задач с использованием теорем сложений и умножения вероятностей" - скачать бесплатно
Презентация по математике "Решение задач с использованием теорем сложений и умножения вероятностей" - скачать бесплатно Параллельный перенос и его свойства
Параллельный перенос и его свойства РЕШЕНИЕ НЕРАВЕНСТВ (НАЙДИ ОШИБКУ) 8 класс
РЕШЕНИЕ НЕРАВЕНСТВ (НАЙДИ ОШИБКУ) 8 класс  Статистический анализ зависимостей между гидрологическими переменными (лекция 10)
Статистический анализ зависимостей между гидрологическими переменными (лекция 10) Закрепление знаний по теме Табличное сложение и вычитание
Закрепление знаний по теме Табличное сложение и вычитание Паросочетания и покрытия. Лекция 13
Паросочетания и покрытия. Лекция 13 Что такое задача
Что такое задача Применение теории вероятностей в анализе спортивных событий
Применение теории вероятностей в анализе спортивных событий Геометрический смысл производной
Геометрический смысл производной