Содержание
- 2. Критерий согласия Критерии согласия – это статистики, которые позволяют проверить соответствие эмпирической и аналитической кривых распределения
- 3. Критерий χ2 (Пирсона) Критерий χ2 был предложен в начале XX Карлом Пирсоном и в настоящее время
- 4. Критерий χ2 (Пирсона) - продолжение Закон распределения данной статистики не зависит от вида исходного распределения и
- 5. Критерий χ2 (Пирсона) - продолжение Гипотеза о соответствии (согласии) эмпирической и аналитической кривых обеспеченностей не опровергается,
- 6. Критерий Колмогорова Мерой отличия эмпирической кривой распределения от теоретической является абсолютное по величине расхождение между эмпирической
- 7. Критерий Колмогорова Недостатки методики: Учитывается только максимальное расхождение между эмпирической и аналитической функциями распределения Наибольшая разность
- 8. Критерий nω2 (Крамера – Мизеса – Смирнова) Тестовой статистикой данного критерия является средний квадрат отклонений между
- 9. Критерий nω2 (Крамера – Мизеса – Смирнова) - 2 Если эмпирическое значение тестовой статистики, вычисленное с
- 10. Критерии случайности Проверка гидрологических рядов на случайность проводится в рамках общей схемы статистической проверки гипотез. В
- 11. Критерий серий Серия – это всякий участок последовательности, состоящий из элементов одного и того же ряда
- 12. Критерий общего числа серий Для проверки гипотезы о том, что данная совокупность сформирована из независимых значений
- 13. Пример расчета методом серий Допустим Qср. = 57,3 м3/с, тогда получим
- 14. Критерий наибольшей длины серий Этот критерий использует в качестве тестовой статистики наибольшую длину серии из элементов
- 15. Критерий числа повышений и понижений Пусть имеется выборка СВ Х: х1, х2, х3 ….хn. Переход от
- 16. Критерий числа экстремумов Экстремум – это элемент последовательности х1, х2, х3 ….хn для которого выполняется одно
- 18. Скачать презентацию















 Презентация по математике "Чтение и запись десятичных дробей" - скачать бесплатно
Презентация по математике "Чтение и запись десятичных дробей" - скачать бесплатно Действия с положительными и отрицательными числами. 6 класс
Действия с положительными и отрицательными числами. 6 класс Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Решение уравнений с помощью систем
Решение уравнений с помощью систем Paātrināta kustība
Paātrināta kustība Принятие решений на основе методов целочисленного программирования
Принятие решений на основе методов целочисленного программирования Лекция 6. Численное интегрирование функций
Лекция 6. Численное интегрирование функций Презентация на тему Перпендикулярные прямые
Презентация на тему Перпендикулярные прямые  Аттестационная работа. Проектно – исследовательская деятельность на уроках математики
Аттестационная работа. Проектно – исследовательская деятельность на уроках математики Формулы середины отрезка и расстояния между двумя точками
Формулы середины отрезка и расстояния между двумя точками Основные понятия математической статистики
Основные понятия математической статистики Решение задач по теме четырехугольники
Решение задач по теме четырехугольники Классическая линейная регрессия
Классическая линейная регрессия Основные этапы решения задач МПЭ
Основные этапы решения задач МПЭ Аттестационная работа. Работа с учащимися над проектом «Математика в быту и повседневной жизни»
Аттестационная работа. Работа с учащимися над проектом «Математика в быту и повседневной жизни» Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм Устная работа
Устная работа Предел функции
Предел функции Презентация по математике "Задачи о русской дружине" - скачать
Презентация по математике "Задачи о русской дружине" - скачать  Статистика – дизайн информации (Алгебра 9 класс)
Статистика – дизайн информации (Алгебра 9 класс) ЕГЭ. Вероятность. Задачи
ЕГЭ. Вероятность. Задачи Презентация по математике "Решение задач с использованием формулы полной вероятности и формулы Бейеса" - скачать бесплатно
Презентация по математике "Решение задач с использованием формулы полной вероятности и формулы Бейеса" - скачать бесплатно Великие женщины математики работу выполнили обучающиеся 6 а класса МОУ СОШ № 34 г.Волжского Волгоградской области Попова Софья и
Великие женщины математики работу выполнили обучающиеся 6 а класса МОУ СОШ № 34 г.Волжского Волгоградской области Попова Софья и  Задачи в стихах. (Часть 1)
Задачи в стихах. (Часть 1) Матрицы и определители
Матрицы и определители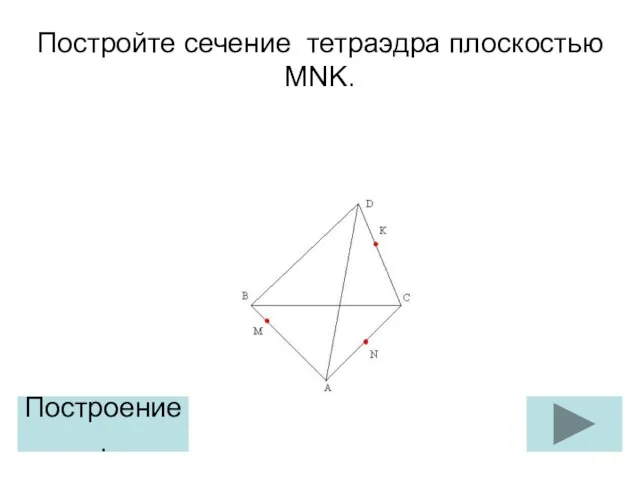 Тетраэдр. Построение сечения (задание 3)
Тетраэдр. Построение сечения (задание 3) Meine heimat
Meine heimat Комплексные числа
Комплексные числа