Regresní a korelační analýza

Regrese a korelace

Regrese charakterizuje průběh závislosti mezi kvantitativními statistickými znaky

Druhy závislostí

Podle počtu kvantitativních znaků
závislost jednoduchá
závislost vícenásobná

Druhy závislostí

Podle typu regresní funkce
lineární závislost
nelineární závislost
Podle směru změn kvantitat. znaků
závislost

Regresní analýza

Základní úkoly regresní analýzy
získání statistických odhadů neznámých parametrů regresní funkce

Základní model
Základní model regresní závislosti
f (xi) …je regresní funkce,
ei

Výběr regresní funkce

Logické posouzení daného vztahu
Vycházíme z grafické analýzy dat
Využití matematicko-statistický

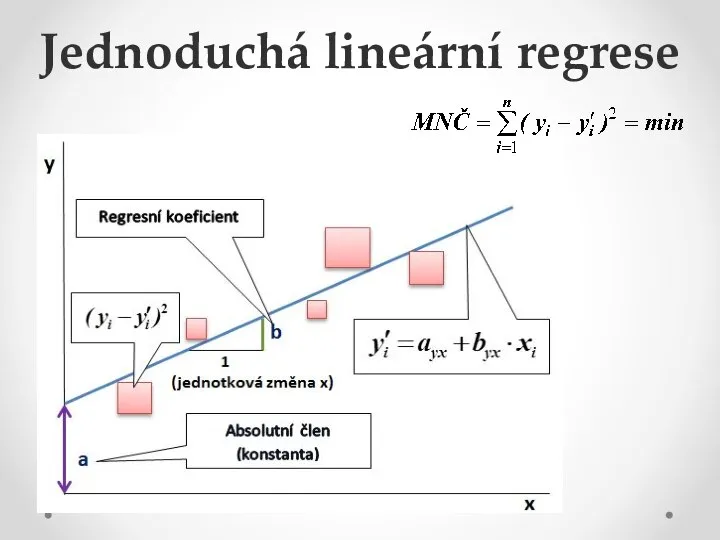
Jednoduchá lineární regrese

Jednoduchá lineární regrese
Model regresní přímky
yi = α +β xi +

Jednoduchá lineární regrese
Metoda nejmenších čtverců vychází z požadavku,
aby součet čtverců

Jednoduchá lineární regrese

Jednostranná závislost – proměnná X je nezávisle
proměnná

Jednoduchá lineární regrese

Korelační analýza
Korelace obecně označuje míru stupně (sílu)
závislosti dvou proměnných X a

Pearsonův koeficient korelace

ryx = rxy
Platí <–1 ≤ r ≤ +1> dvě

Korelační analýza

Koeficient determinace r2yx je druhou mocninou koeficientu korelace.

r2

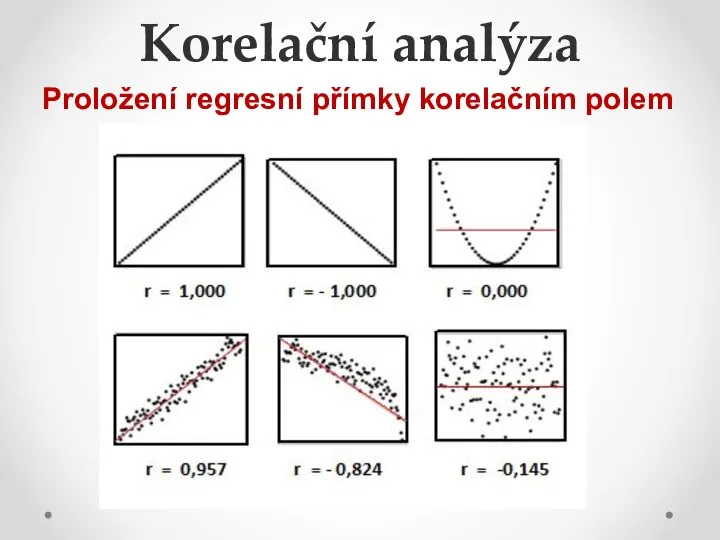
Korelační analýza

Proložení regresní přímky korelačním polem

Spearmanův koeficient pořadí

Spearmanův koeficient korelace rs nabývá
hodnot z