Содержание
- 2. Упорядоченные множества. Перестановки и размещения Множество называется упорядоченным. Если каждому элементу множества противопоставлено некоторое число от
- 3. Варианты перестановок множества Пусть задано множество А из n – элементов, а Pn – число перестановок.
- 4. Примеры Задача 1. Сколькими способами можно поставить 4 книги на полке. Задача 2. Сколькими способами можно
- 5. Перестановки данного множества Задача 3. Сколько можно составить перестановок из n элементов, в которых данные два
- 6. РЕШЕНИЕ ЗАДАЧИ 3 Шаг 1.Определим число перестановок, в которых a и b стоят рядом. Шаг 2.
- 7. РЕШЕНИЕ ЗАДАЧИ 3 Шаг 5. Таким образом число перестановок в которых a и b стоят рядом
- 8. Задача Задача 4. Сколькими способами можно расположить 8 ладей на шахматной доске так , чтобы они
- 9. Задача 4 Ответ: n! = 8! = 40320
- 10. Упорядоченные подмножества данного множества Задано множество А. ВОПРОС: Сколько можно получить упорядоченных подмножеств данного множества? 1.
- 11. Упорядоченные подмножества данного множества ТЕОРЕМА: Число упорядоченных k- элементных подмножеств множества из n элементов равно: Это
- 12. Задача 5 Сколько способов размещения 4 студентов на 25 местах.
- 13. Ответ задачи 5
- 14. Задача 6 Студенту необходимо сдать 4 экзамена в течении 8 дней. Сколько существует вариантов? А если
- 15. Ответы задачи 6 1 2
- 16. Перестановки с повторениями ВОПРОС: Сколько способов разложения множества А, состоящего из n элементов, на сумму множеств
- 17. Перестановки с повторениями Согласно правила умножения количество возможных перестановок равно: ИЗ этого получается следующая теорема
- 18. ТЕОРЕМА А именно, сколько можно составить слов из заданного алфавита?
- 19. Полиномиальные коэффициенты ЗАДАЧА 7. Число слов, которые можно получить из перестановки букв слова МАТЕМАТИКА.
- 20. Ответ задачи 7 ОТВЕТ 10!/(2!*3!*2!)=151200
- 21. Задача 8. Число слов, которые можно составить из 12 букв (4 буквы а; 4 буквы б;
- 22. Ответ на задачу 8 12! / (4!*4!*2!*2!) = 207900
- 23. Взаимно-однозначное соответствие Пусть заданы два множества А и B. Будем считать, что между двумя множествами установлено
- 24. Взаимно-однозначное соответствие? ПРИМЕР 1. А – множество студентов B – множество парт. Каждому студенту, соответствует стол,
- 25. Взаимно-однозначное соответствие? ПРИМЕР 2: А – множество жителей г. Владимира. В – множество домов в городе.
- 26. ПРИМЕР 3. Каждому элементу упорядоченного множества А из n элементов, соответствует свой номер. Взаимно-однозначное соответствие?
- 27. Эквивалентность множеств ОПРЕДЕЛЕНИЕ. Множества, для которых существует взаимно-однозначное соответствие называются эквивалентными. ТЕОРЕМА. Для того, чтобы два
- 28. Эквивалентность множеств
- 29. Эквивалентность множеств Использование следствия эквивалентности для вычисления числа Элементов множества.
- 30. Сочетания с повторениями ОПРЕДЕЛЕНИЕ. Сочетаниями из m элементов по n элементам с повторениями называют группы, содержащие
- 31. Теорема вычисления сочетаний с повторениями Ответ: aa,ac,bc,ab,bb,сс – итого 6. ТЕОРЕМА. Число различных сочетаний из m
- 32. Задача 7 Кости домино можно рассматривать как сочетание с повторениями по два элемента из семи цифр
- 33. Задача 8 В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и картошка. Сколькими способами
- 34. Бином Ньютона Равенство 1 называют биномом Ньютона Биноминальный коэффициент
- 35. Бином Ньютона Формулу бинома Ньютона можно свернуть до вида:
- 36. Треугольник Паскаля Бесконечная таблица Биномиальных коэффициентов
- 37. Закономерности треугольника Паскаля Числа треугольника симметричны (равны) относительно вертикальной оси. В строке с номером n: первое
- 38. Полиномиальная теорема
- 39. Полиномиальная теорема и бином Ньютона Это и есть бином Ньютона
- 41. Скачать презентацию






































 Цилиндр. Общее определение цилиндрического тела
Цилиндр. Общее определение цилиндрического тела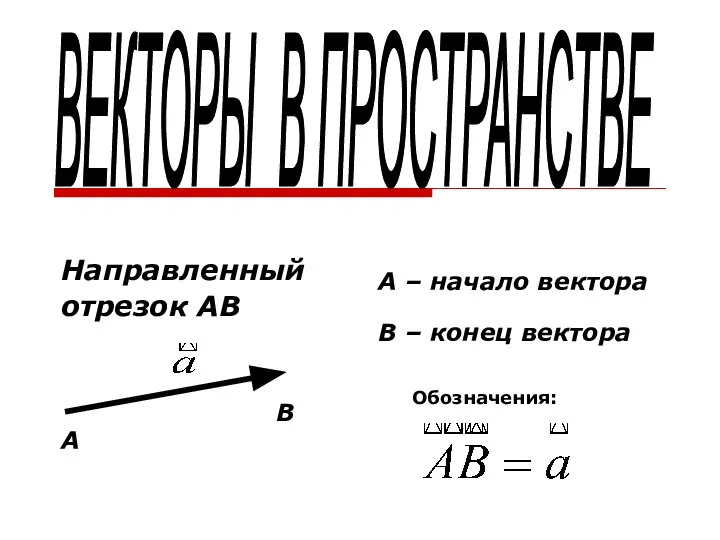 Векторы в пространстве
Векторы в пространстве Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Законы арифметических действий. Решение задач
Законы арифметических действий. Решение задач Числовые промежутки
Числовые промежутки ТЕСТ по математике
ТЕСТ по математике Frekvenční přenos
Frekvenční přenos Интерактивный тренажёр Найди значения выражений. Часть 3
Интерактивный тренажёр Найди значения выражений. Часть 3 Вступ до математичного аналізу. Поняття функції однієї змінної. Методи побудови графіків функцій без використання похідної
Вступ до математичного аналізу. Поняття функції однієї змінної. Методи побудови графіків функцій без використання похідної Модель множественной линейной регрессии
Модель множественной линейной регрессии Тема урока: Действия с обыкновенными дробями
Тема урока: Действия с обыкновенными дробями Решение систем уравнений второй степени способом подстановки
Решение систем уравнений второй степени способом подстановки Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Урок математики
Урок математики  Тест по теме: "Перпендикулярность в пространстве". Практическая часть
Тест по теме: "Перпендикулярность в пространстве". Практическая часть Bisector, median, height of the triangle
Bisector, median, height of the triangle Векторы на плоскости
Векторы на плоскости Решение задач на применение теоремы Пифагора
Решение задач на применение теоремы Пифагора Диференціальні рівняння. Загальні визначення (лекція 4)
Диференціальні рівняння. Загальні визначення (лекція 4) Леонард Эйлер Идеальный математик XVII века
Леонард Эйлер Идеальный математик XVII века  Фигуры планиметрии
Фигуры планиметрии Координатный луч
Координатный луч Многочлен и его стандартный вид
Многочлен и его стандартный вид Удмуртия Презентация МБОУ «СОШ №4» 8а класса Ворончихиной Евгении
Удмуртия Презентация МБОУ «СОШ №4» 8а класса Ворончихиной Евгении Работа с текстом на уроках математики
Работа с текстом на уроках математики Площадь треугольника. Теоремы, следствия и задачи
Площадь треугольника. Теоремы, следствия и задачи Предел последовательности. Пример вычисления предела
Предел последовательности. Пример вычисления предела Измерения, погрешности и точности
Измерения, погрешности и точности