Содержание
- 2. Если ты услышишь, что кто-то не любит математику, не верь. Её нельзя не любить - её
- 3. Цель реферата: Научиться правильно отображать формулы с применением различных способов решения уравнений Задачи реферата: - улучшить
- 4. История квадратных уравнений Необходимость решать уравнения еще в древности была вызвана потребностью решать задачи, связанные с
- 6. Решение уравнений способом «переброски» Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета
- 7. Свойства коэффициентов квадратного уравнения А. ах2 + bх + с = 0, а ≠ 0 1.Если
- 8. Свойства коэффициентов квадратного уравнения А. ах2 + bх + с = 0, а ≠ 0 2.
- 9. Свойства коэффициентов квадратного уравнения Б. ах2 + bх + с = 0, а ≠ 0 Если
- 10. Свойства коэффициентов квадратного уравнения В. уравнение x2 + px + q = 0 совпадает с уравнением
- 11. По теореме о секущих имеем ОВ∙ОD = ОА ∙ ОС, откуда ОС = Центр окружности находиться
- 12. 1. Радиус окружности больше ординаты центра (AS > SK, или R > ), окружность пересекает ось
- 13. Радиус окружности равен ординате центра (AS = SВ, или R = ), окружность касается оси Ох
- 14. Радиус окружности меньше ординаты центра (AS R AS Нет решения S A B Решение квадратных уравнений
- 15. 1. Радиус окружности больше ординаты центра (AS > SK, или R > ), окружность пересекает ось
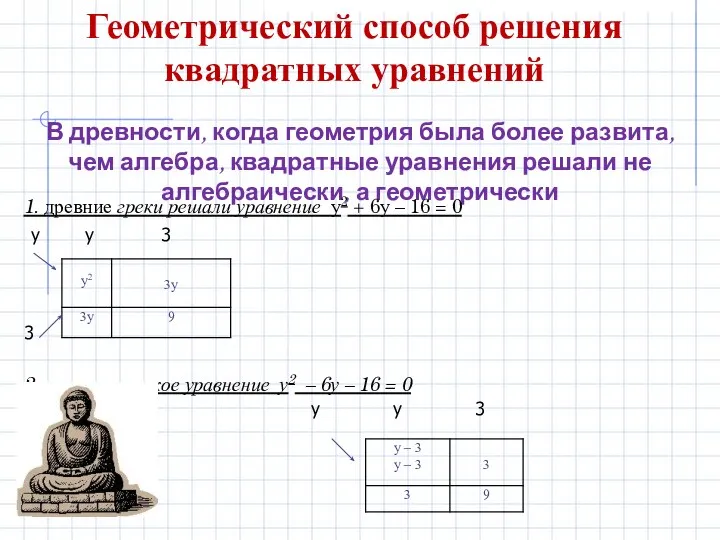
- 16. Геометрический способ решения квадратных уравнений В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения
- 17. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств
- 18. методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников
- 20. Скачать презентацию
















 Фракталы
Фракталы Головоломки мира
Головоломки мира Площадь треугольника
Площадь треугольника Умножение многочлена на многочлен
Умножение многочлена на многочлен Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Подготовка к контрольной работе
Подготовка к контрольной работе Деление окружности на равные части
Деление окружности на равные части Многогранники. Урок-лекция
Многогранники. Урок-лекция Занимательная математика
Занимательная математика Декартовы координаты на плоскости (решение задач)
Декартовы координаты на плоскости (решение задач) Решение задач в два действия. 1 класс
Решение задач в два действия. 1 класс Уңай һәм тискәре саннар
Уңай һәм тискәре саннар Деление десятичных дробей на натуральное число
Деление десятичных дробей на натуральное число Синтез оптимальных дискретных детерминированных систем. Нахождение оптимального программного управления (лекция 2)
Синтез оптимальных дискретных детерминированных систем. Нахождение оптимального программного управления (лекция 2) Решение задач с параметрами
Решение задач с параметрами Прямая на плоскости
Прямая на плоскости Неполные квадратные уравнения
Неполные квадратные уравнения Средние величины и показатели вариации
Средние величины и показатели вариации The Distribution of Molecules over Velocities Maxwell Distribution
The Distribution of Molecules over Velocities Maxwell Distribution Деление с остатком
Деление с остатком Игра. Сосчитай зайчиков (начальная школа)
Игра. Сосчитай зайчиков (начальная школа) Применение систем нечеткой логики
Применение систем нечеткой логики Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений Средние величины в статистике
Средние величины в статистике Проверка статистических гипотез. (Лекция 4)
Проверка статистических гипотез. (Лекция 4) Деление дробей. Делимое. Взаимо обратные
Деление дробей. Делимое. Взаимо обратные К чему может привести знание свойств линейной функции. Учебный проект
К чему может привести знание свойств линейной функции. Учебный проект Решение дробно-рациональных уравнений с модулем
Решение дробно-рациональных уравнений с модулем