Содержание
- 2. Системи лінійних алгебраїчних рівнянь Систему алгебраїчних рівнянь називають лінійною, якщо вона може бути записана у вигляді
- 3. - розширена матриця С.Л.А.Р.. стовпець вільних членів стовпець невідомих; - основна матриця С.Л.А.Р Системи лінійних алгебраїчних
- 4. Системи лінійних алгебраїчних рівнянь Розв’язком системи називають множину дійсних чисел с1, с2, …, сn , підстановка
- 5. Переваги застосування метода Гаусса: 1) дозволяє дослідити систему на сумісність; 2) у випадку сумісності знайти іі
- 6. . (Е.П.) матриці називають перетворення слідуючого вигляду: відкидання нульового рядка (стовпця); множення всіх елементів рядка (стовпця)
- 7. Мінором k-го порядку матриці називають визначник порядку k, який отримують викресленням будь-яких рядків і стовпців з
- 8. Мінор матриці Приклад 1 (продовження )
- 9. Рангом матриці А називають найвищий порядок її ненульового мінора. Позначення: rang(A), r(A) Властивості rang(A) r(A) ≤
- 10. Приклад 2 Обчислити ранг матриці А за допомогою Е.П. Ранг матриці А = внаслідок того, що
- 11. Ранг матриці Розв’язок
- 12. Система m лінійних рівнянь з n невідомими сумісна тоді і тільки тоді, коли r(A) = r(A)
- 13. метод Гаусса Суть метода Гаусса полягає в тому , що шляхом елементарних перетворень С.Л.А.Р. приводять до
- 14. Приклад 3 Дослідити систему рівнянь на сумісність і у випадку сумісності знайти розв’язки метод Гаусса Розв’язок
- 15. метод Гаусса Приклад 3 (продовження ) ~ 0 = -16 Отже, початкова система несумісна. б) r(A)
- 16. метод Гаусса Приклад 3 (продовження ) Розв’язок ~ ~ ~ ~ ~ ~ . r(A) =
- 17. метод Гаусса Приклад 3 (продовження ) в) Розв’язок ~ ~
- 18. метод Гаусса Приклад 3 (продовження ) r(A) = r(A) = 3 Система сумісна і невизначена. Вважаємо
- 19. Системи n лінійних рівнянь з n невідомими Якщо то r(A) = r(A) = n (кількість рівнянь
- 20. Цей визначник отримано шляхом послідовної заміни j-го стовпця визначника ∆ стовпцем чисел b1 , b2 ,
- 21. Приклад 4 Розв’язати систему лінійних алгебраїчних рівнянь за формулами Крамера: Розв’язок ∆ ≠ 0, можемо застосувати
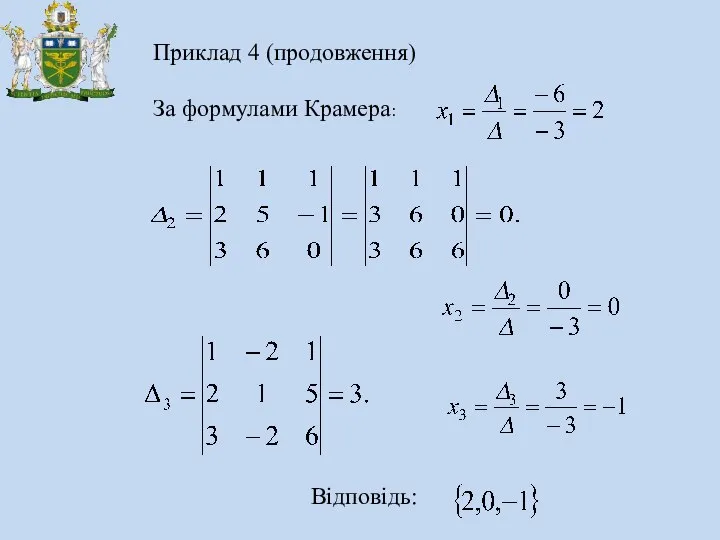
- 22. Приклад 4 (продовження) За формулами Крамера: Відповідь:
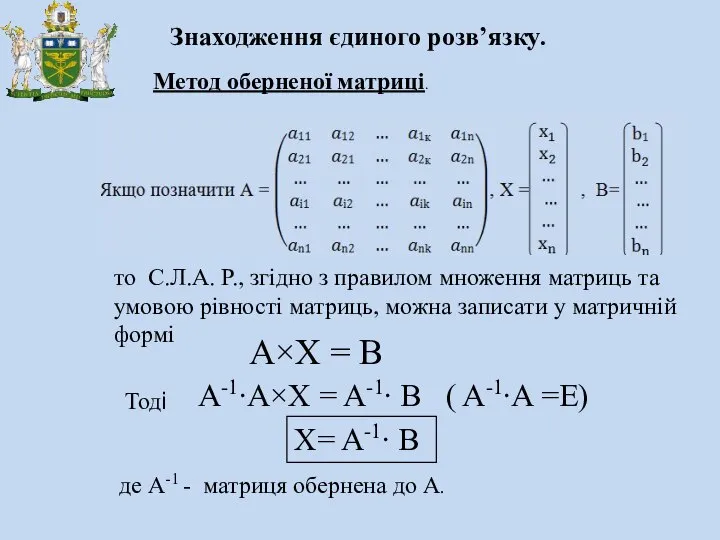
- 23. Метод оберненої матриці. то С.Л.А. Р., згідно з правилом множення матриць та умовою рівності матриць, можна
- 24. Приклад 5 Розв’язати C.Л.А.Р. методом оберненої матриці Запишемо систему рівнянь у вигляді матричного рівняння Розв’язок де
- 25. Приклад 5 (продовження ) Визначник матриці А не дорівнює нулю, тому існує А-1 і розвязок можна
- 26. Приклад 5 (продовження) Записуємо обернену матрицю до матриці А
- 27. Приклад 5 (продовження) Відповідь: .
- 29. Скачать презентацию
























 Прославленное число Шахерезады 1001
Прославленное число Шахерезады 1001 Преобразование квадратных корней
Преобразование квадратных корней Логарифмы вокруг нас
Логарифмы вокруг нас Презентация на тему Сложение и вычитание чисел
Презентация на тему Сложение и вычитание чисел  Применение производной к исследованию функции
Применение производной к исследованию функции Геометрические тела
Геометрические тела Задачи на построение
Задачи на построение Предикаты и кванторы. Действия над предикатами и их свойства
Предикаты и кванторы. Действия над предикатами и их свойства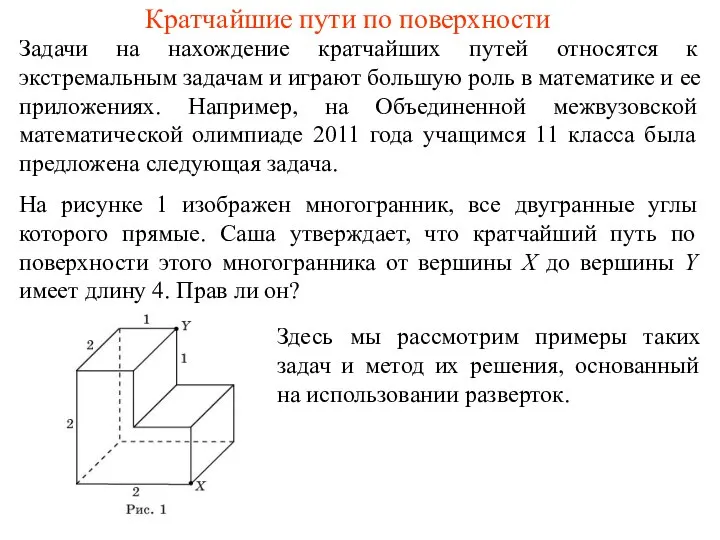 Кратчайшие пути на поверхности
Кратчайшие пути на поверхности Статистические гипотезы и достоверность статистических характеристик
Статистические гипотезы и достоверность статистических характеристик Моделирование выборочных данных суммой экспоненциальных функций Лекция 12
Моделирование выборочных данных суммой экспоненциальных функций Лекция 12 Приближение модели LES моделью Gabls методами Луиса и Эзау
Приближение модели LES моделью Gabls методами Луиса и Эзау Жай бөлшектерді қосу және азайту
Жай бөлшектерді қосу және азайту Пересекающиеся плоскости
Пересекающиеся плоскости Свойства числовых неравенств
Свойства числовых неравенств Скрещивающиеся прямые
Скрещивающиеся прямые Элементарные функции
Элементарные функции Определение квадратного уравнения. Неполные квадратные уравнения
Определение квадратного уравнения. Неполные квадратные уравнения Статистические оценки параметров распределения
Статистические оценки параметров распределения Теория предикатов. Операции над предикатами
Теория предикатов. Операции над предикатами Деление обыкновенных дробей. 6 класс
Деление обыкновенных дробей. 6 класс Решение задач по теме «Многогранники».
Решение задач по теме «Многогранники».  Нумерация чисел от 1 до 100. Тест
Нумерация чисел от 1 до 100. Тест ДРУЖОК правила по математике для начальных классов
ДРУЖОК правила по математике для начальных классов Призма. Элементы призмы
Призма. Элементы призмы Решение уравнений и задач при помощи уравнений
Решение уравнений и задач при помощи уравнений Линии. 5 класс
Линии. 5 класс Випадкова подія. Ймовірність випадкової події. (6 клас)
Випадкова подія. Ймовірність випадкової події. (6 клас)