Системы линейных алгебраических уравнений

Сентябрь 13, 2022

Главная
Математика
Системы линейных алгебраических уравнений

Содержание

2. Системы любого числа линейных алгебраических уравнений О п р е д е л е н и
3. Системы любого числа линейных алгебраических уравнений где a11,…,amn, b1,…,bm некоторые числа. Если b1=0,….,bm=0, то система называется
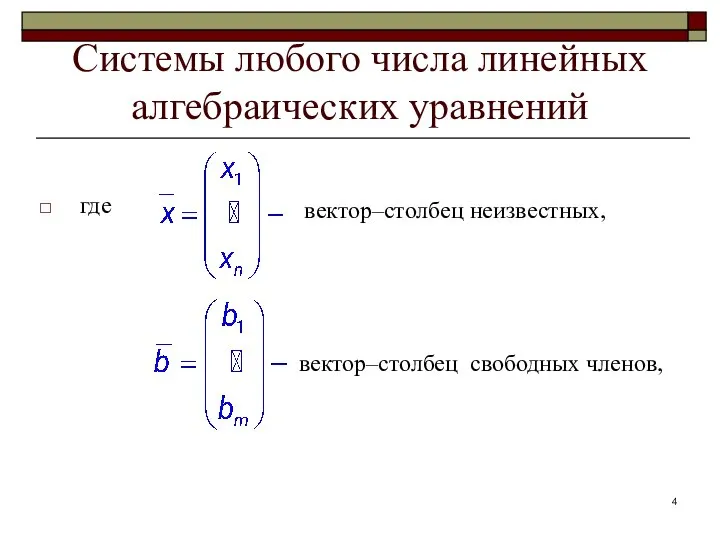
4. Системы любого числа линейных алгебраических уравнений где вектор–столбец неизвестных, вектор–столбец свободных членов,
5. Системы любого числа линейных алгебраических уравнений О п р е д е л е н и
6. Системы любого числа линейных алгебраических уравнений О п р е д е л е н и
7. Системы любого числа линейных алгебраических уравнений О п р е д е л е н и
8. Системы любого числа линейных алгебраических уравнений Т е о р е м а 2. Решение системы
9. Системы любого числа линейных алгебраических уравнений Метод Гаусса Для решения системы (2) с матрицей А размерности
10. Системы любого числа линейных алгебраических уравнений - система совместна, - базисными неизвестными объявить те, номера которых
11. Системы любого числа линейных алгебраических уравнений 3) Привести ступенчатую матрицу, полученную при выполнении шага 1), к
12. Системы любого числа линейных алгебраических уравнений З а м е ч а н и е 2.
13. ПРИМЕРЫ П р и м е р 1. Для системы: указать матрицу системы А и столбец
14. ПРИМЕРЫ Тогда матрица А рассматриваемой системы составляется из числовых коэффициентов, стоящих в системе при неизвестных:
15. ПРИМЕРЫ Столбец составляется из свободных членов системы: Поэтому систему можно переписать в векторной форме: О т
16. ПРИМЕРЫ П р и м е р 2. Исследовать на совместность систему: Р е ш е
17. ПРИМЕРЫ Выполним шаг 1) метода Гаусса: Следовательно: и О т в е т: система несовместна.
18. ПРИМЕРЫ П р и м е р 3. Решить систему: Р е ш е н и
19. ПРИМЕРЫ
20. ПРИМЕРЫ О т в е т:
21. ПРИМЕРЫ П р и м е р 4. Исследовать на совместность и решить систему:
22. ПРИМЕРЫ Р е ш е н и е. Воспользуемся методом Гаусса: составим матрицу А рассматриваемой системы,
23. ПРИМЕРЫ
24. ПРИМЕРЫ
26. Скачать презентацию

Слайд 2

Системы любого числа линейных алгебраических уравнений
О п р е д е

л е н и е 1. Системой линейных алгебраических уравнений, состоящей из m уравнений с n неизвестными х1,…,хn, называется система вида:

(1)

Слайд 3

Системы любого числа линейных алгебраических уравнений
где a11,…,amn, b1,…,bm некоторые числа. Если

b1=0,….,bm=0, то система называется линейной однородной. В противном случае система (1) называется линейной неоднородной системой.
З а м е ч а н и е 1. Система (1) может быть записана в векторной форме:

(2)

Слайд 4

Системы любого числа линейных алгебраических уравнений
где
вектор–столбец неизвестных,
вектор–столбец свободных членов,

Слайд 5

Системы любого числа линейных алгебраических уравнений
О п р е д е

л е н и е 2. Расширенной матрицей системы (1) называется матрица, обозначаемая и полученная приписыванием к матрице А справа после вертикальной черты столбца .

матрица системы.

Слайд 6

Системы любого числа линейных алгебраических уравнений
О п р е д е

л е н и е 3. Решением системы (2) называется любой n- мерный вектор подстановка которого в (2) дает тождество.

Слайд 7

Системы любого числа линейных алгебраических уравнений
О п р е д

е л е н и е 4. Система называется совместной, если она имеет хотя бы одно решение. В противном случае система называется несовместной.
Т е о р е м а 1. (Кронекера – Капелли). Система (1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы, то есть:
При этом если то система имеет единственное решение; если то система имеет бесконечное множество решений (n –число неизвестных).

Слайд 8

Системы любого числа линейных алгебраических уравнений
Т е о р е м

а 2. Решение системы (2) имеет вид:
где частное решение линейной неоднородной системы (2); число k, называемое числом свободных неизвестных системы (2), вычисляется по формуле
произвольные постоянные числа; постоянные n- мерные векторы, являющиеся линейно независимыми решениями соответствующей линейной однородной системы .

(3)

Слайд 9

Системы любого числа линейных алгебраических уравнений
Метод Гаусса
Для решения системы (2)

с матрицей А размерности mxn и столбцом свободных членов нужно выполнить следующие действия:
1) Составить расширенную матрицу и привести ее к ступенчатому виду с помощью элементарных преобразований строк;
2) Если записать ответ: система несовместна.
Если сделать выводы:

Слайд 10

Системы любого числа линейных алгебраических уравнений
- система совместна,
- базисными неизвестными объявить

те, номера которых совпадут с номерами базисных столбцов ступенчатого вида матрицы А, содержащих опорные элементы этой матрицы; остальные неизвестные объявить свободными,
- число свободных неизвестных равно ,
- перейти к выполнению следующего шага;

Слайд 11

Системы любого числа линейных алгебраических уравнений
3) Привести ступенчатую матрицу, полученную

при выполнении шага 1), к виду Гаусса;
4) Написать систему линейных уравнений, соответствующую матрице, построенной на шаге 3), обозначив свободные неизвестные ;
5) Выразить из полученной системы базисные неизвестные через свободные неизвестные;
6) Записать ответ, воспользовавшись или векторной формой записи (5), или координатной формой:

Слайд 12