Содержание
- 2. Достаточное условие существования определенного интеграла Если на отрезке [a,b] функция y=f(x) непрерывна, то она интегрируема на
- 3. Свойства определенного интеграла 1 Постоянный множитель можно выносить за знак определенного интеграла.
- 4. Доказательство: Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим интегральную сумму: Переходим к пределу в
- 5. Следовательно по определению:
- 6. 2 Определенный интеграл от алгебраической суммы (разности) двух функций равен сумме (разности) интегралов от этих функций.
- 7. 3 Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов по
- 8. Геометрически это означает, что если a
- 9. S S S
- 10. 4 Если на [a,b], где a то
- 11. Доказательство: Пусть фиксировано разбиение отрезка [a,b] и выбор точек то для интегральных сумм: Если Переходим к
- 12. Следствие. Пусть на [a,b], где a где m и M некоторые числа. Тогда
- 13. Доказательство: По свойству 4 имеем: По свойству 1 и геометрическому смыслу определенного интеграла:
- 14. 5 Если на [a,b], где a Теорема о среднем что
- 15. Доказательство: По свойству функции, непрерывной на отрезке, для произвольного значения справедливо неравенство: Где m и М
- 16. Но функция, непрерывная на отрезке, принимает любое значение, заключенное между ее наименьшим и наибольшим значениями, поэтому
- 17. Пусть Тогда теорема о среднем утверждает, что найдется такая точка что площадь под кривой y=f(x) на
- 19. Равенство называется формулой среднего значения. называется средним значением функции.
- 21. Скачать презентацию
![Достаточное условие существования определенного интеграла Если на отрезке [a,b] функция y=f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463571/slide-1.jpg)

![Доказательство: Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим интегральную](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463571/slide-3.jpg)




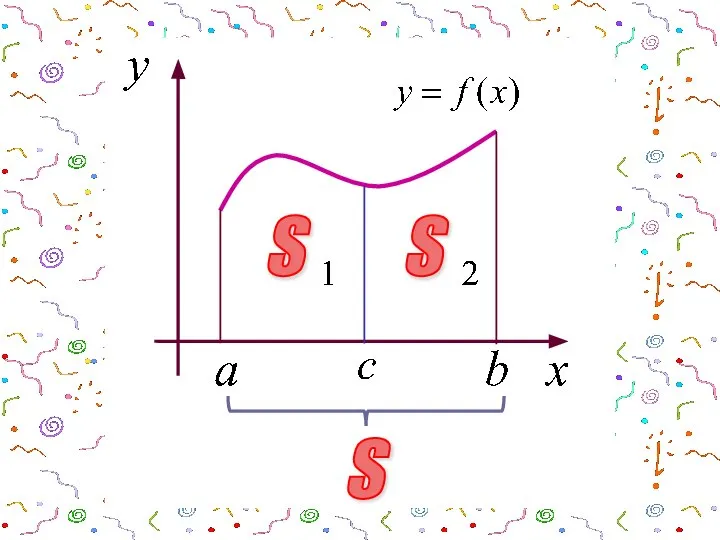
![4 Если на [a,b], где a то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463571/slide-9.jpg)
![Доказательство: Пусть фиксировано разбиение отрезка [a,b] и выбор точек то для](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463571/slide-10.jpg)
![Следствие. Пусть на [a,b], где a где m и M некоторые числа. Тогда](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463571/slide-11.jpg)

![5 Если на [a,b], где a Теорема о среднем что](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463571/slide-13.jpg)



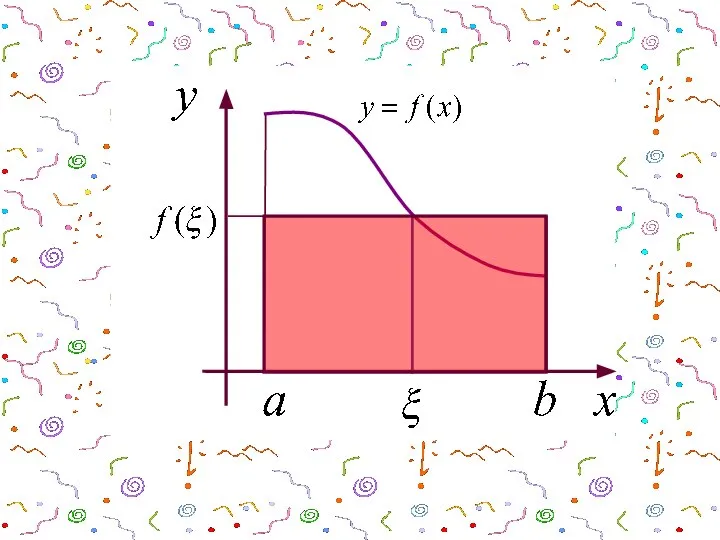

 Решение уравнений. ГИА 2014 Модуль «Алгебра» №4
Решение уравнений. ГИА 2014 Модуль «Алгебра» №4 Ф.И. Класс Тема урока
Ф.И. Класс Тема урока Диагонали четырёхугольников
Диагонали четырёхугольников Моделирование информационных систем. Примеры систем
Моделирование информационных систем. Примеры систем Параллельные прямые. Материалы к уроку
Параллельные прямые. Материалы к уроку Площади параллелограмма, треугольника и трапеции. Урок 20
Площади параллелограмма, треугольника и трапеции. Урок 20 Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов)
Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов) МОУ Афанасьевская СОШ Урок математики в 1 классе Тема: «Прибавление числа 4» Подготовила
МОУ Афанасьевская СОШ Урок математики в 1 классе Тема: «Прибавление числа 4» Подготовила  Презентация по математике "Язык уравнений" - скачать бесплатно
Презентация по математике "Язык уравнений" - скачать бесплатно Компланарные векторы
Компланарные векторы Линейная функция. Построение графика функции у= 2х-1
Линейная функция. Построение графика функции у= 2х-1 Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов Решение задач с помощью квадратных уравнений (по материалам Бородинского сражения)
Решение задач с помощью квадратных уравнений (по материалам Бородинского сражения) Организационный момент Французский писатель 19 века Анатоль Франс однажды заметил: «Учиться можно только весело. Чтобы пе
Организационный момент Французский писатель 19 века Анатоль Франс однажды заметил: «Учиться можно только весело. Чтобы пе Умножение десятичных дробей
Умножение десятичных дробей Признаки равенства треугольников
Признаки равенства треугольников Основные понятия теории вероятностей
Основные понятия теории вероятностей Свойства алгоритма
Свойства алгоритма Элементы прикладной математики
Элементы прикладной математики Решение СЛАУ методом Гаусса
Решение СЛАУ методом Гаусса Случайные события и их вероятности
Случайные события и их вероятности Разложение квадратного трёхчлена на множители
Разложение квадратного трёхчлена на множители Тест. Векторы. Сумма векторов. Умножение вектора на число. 10 класс
Тест. Векторы. Сумма векторов. Умножение вектора на число. 10 класс Знаменитые математики в истории комплексных чисел Выполнил ученик класса и-10-1 Маслов Геннадий
Знаменитые математики в истории комплексных чисел Выполнил ученик класса и-10-1 Маслов Геннадий Метрологические характеристики МКХА
Метрологические характеристики МКХА Лекции по теории функции комплексной переменной
Лекции по теории функции комплексной переменной Задача на вычисление производной
Задача на вычисление производной Измерительные шкалы
Измерительные шкалы