Содержание
- 2. 2. Системы линейных уравнений
- 3. Понятие СЛУ Система m линейных уравнений с n переменными имеет вид: В кратком виде такую систему
- 4. Виды СЛУ СЛУ называется совместной, если она имеет хотя бы одно решение. Если решений нет, то
- 5. СЛУ в матричной форме Матрицей системы называется матрица коэффициентов при переменных:
- 6. СЛУ в матричной форме Матрица-столбец неизвестных: Матрица-столбец свободных членов (правых частей): Тогда СЛУ можно записать в
- 7. Метод обратной матрицы Пусть в СЛУ AX = B матрица A квадратная и невырожденная. Тогда для
- 8. Метод расширенной матрицы Составим расширенную матрицу системы (A|B). Элементарными преобразованиями строк расширенной матрицы приведем матрицу A
- 9. Метод Крамера Теорема Крамера: Пусть матрица СЛУ квадратная и невырожденная. Пусть |Ai| – определитель матрицы, получаемой
- 10. Элементарные преобразования в СЛУ Теорема (о равносильности СЛУ): При любых элементарных преобразованиях строк расширенной матрицы СЛУ
- 11. Метод Гаусса Построим для СЛУ расширенную матрицу. С помощью элементарных преобразований приведем расширенную матрицу к ступенчатому
- 12. Совместность СЛУ Теорема Кронекера-Капелли (о совместности СЛУ): СЛУ совместна тогда и только тогда, когда ранг матрицы
- 13. Базисные переменные Пусть ранг r расширенной матрицы СЛУ меньше числа переменных. В этом случае СЛУ имеет
- 14. Базисные решения Если эта матрица невырождена, то выбранные переменные называются основными или базисными. Оставшиеся переменные называются
- 15. Однородные СЛУ Однородная СЛУ всегда совместна (как минимум, имеется нулевое решение). Для существования ненулевых решений ранг
- 16. Фундаментальные решения Совокупность линейно независимых решений однородной СЛУ называется фундаментальной, если любое возможное решение этой СЛУ
- 18. Скачать презентацию















 Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Последовательности. Арифметическая и геометрическая прогрессии
Последовательности. Арифметическая и геометрическая прогрессии Презентация к уроку математики по теме «Отношения и пропорции» Автор: учитель математики школы № 436 Иванова Е.С.
Презентация к уроку математики по теме «Отношения и пропорции» Автор: учитель математики школы № 436 Иванова Е.С. Чисельні методи. Елементи теорії похибок. (Лекція 1)
Чисельні методи. Елементи теорії похибок. (Лекція 1) Способы умножения натуральных чисел
Способы умножения натуральных чисел Урок математики в 1 классе На тему : Число 0. Составила ЛАПШИНА ГАЛИНА МАТВЕЕВНА, учитель начальных классов МО
Урок математики в 1 классе На тему : Число 0. Составила ЛАПШИНА ГАЛИНА МАТВЕЕВНА, учитель начальных классов МО Аттестационная работа. Образовательная программа элективного курса - Занимательная математика
Аттестационная работа. Образовательная программа элективного курса - Занимательная математика Аттестационная работа. Методическая разработка по выполнению проекта «Таблица умножения с увлечением»
Аттестационная работа. Методическая разработка по выполнению проекта «Таблица умножения с увлечением» Измерения
Измерения Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Подготовка учащихся к городскому туру олимпиады по математике 2009-2010 уч. г.
Подготовка учащихся к городскому туру олимпиады по математике 2009-2010 уч. г. Аттестационная работа. Элективный курс по математике Избранные вопросы математики. (8 класс)
Аттестационная работа. Элективный курс по математике Избранные вопросы математики. (8 класс) Числа и вычисления. Теория
Числа и вычисления. Теория Задача экономического содержания в ЕГЭ № 19
Задача экономического содержания в ЕГЭ № 19 Частотная таблица
Частотная таблица Презентация по математике "Метод графов" - скачать
Презентация по математике "Метод графов" - скачать 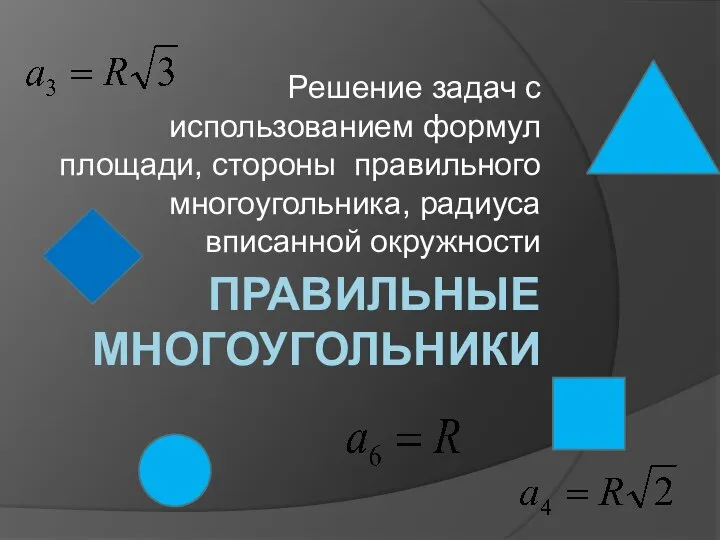 Решение задач с использованием формул площади, стороны многоугольника, радиуса вписанной окружности. Правильные многоугольники
Решение задач с использованием формул площади, стороны многоугольника, радиуса вписанной окружности. Правильные многоугольники УРОК-ПРОЕКТ УРОК-ПРОЕКТ Работу выполнила учитель математики МКОУ ООШ с.Ку
УРОК-ПРОЕКТ УРОК-ПРОЕКТ Работу выполнила учитель математики МКОУ ООШ с.Ку Текстовая задача и процесс ее решения
Текстовая задача и процесс ее решения 11 марта. Классная работа.
11 марта. Классная работа. Площадь
Площадь Аттестационная работа. Проектно – исследовательская деятельность на уроках математики
Аттестационная работа. Проектно – исследовательская деятельность на уроках математики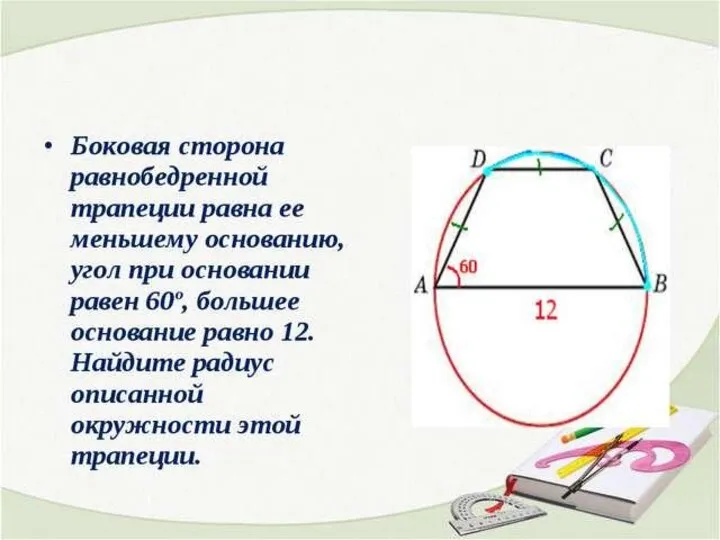 Боковая сторона равнобедренной трапеции
Боковая сторона равнобедренной трапеции Методы решения систем уравнений второй степени. 9 класс
Методы решения систем уравнений второй степени. 9 класс Комплексные числа
Комплексные числа Умножение двучлена на двучлен
Умножение двучлена на двучлен Площади параллелограмма, треугольника, трапеции. Подготовка к ГИА
Площади параллелограмма, треугольника, трапеции. Подготовка к ГИА Функция. Предел функции
Функция. Предел функции