Содержание
- 2. Запись числа в стандартном виде В науке и технике встречаются как очень большие, так и очень
- 3. Рассмотрим примеры: Скорость света 300 000 000 м/с
- 4. Рассмотрим примеры: Скорость света 3 00 000 000 м/с 8 нулей
- 5. Рассмотрим примеры: Скорость света 3 00 000 000 м/с = 3 ∙ 108 м/с 8 нулей
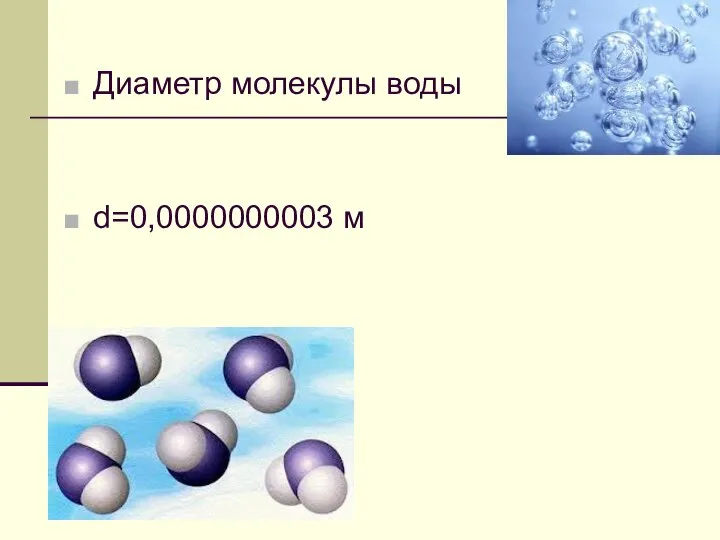
- 6. Диаметр молекулы воды d=0,0000000003 м
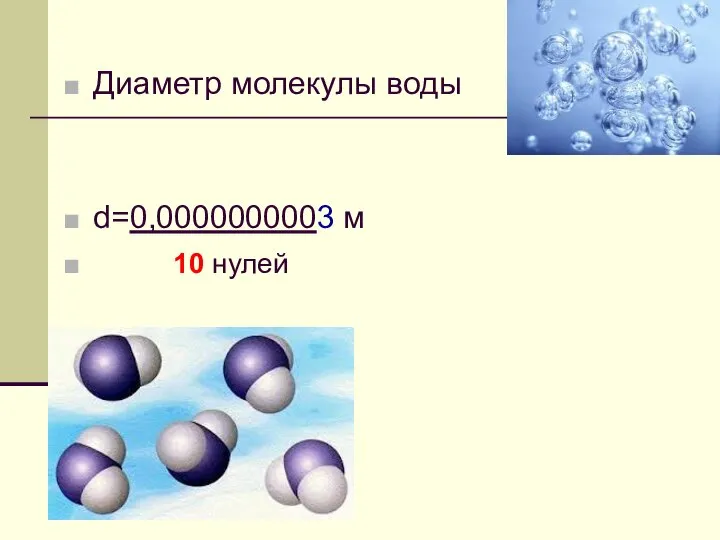
- 7. Диаметр молекулы воды d=0,0000000003 м 10 нулей
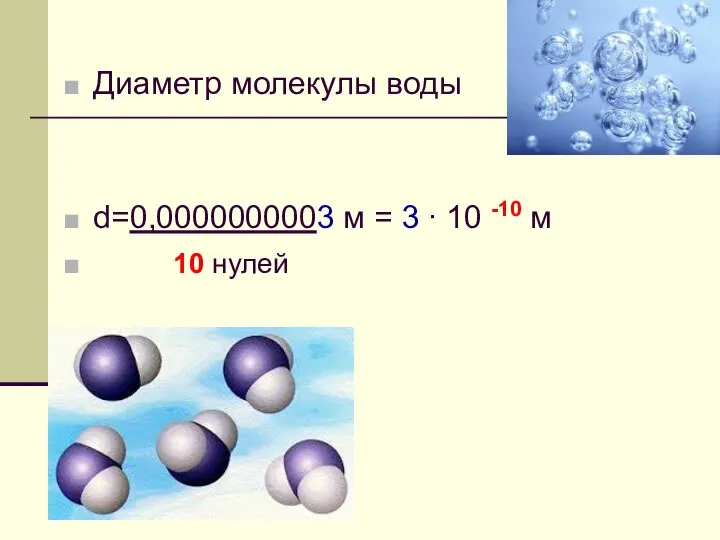
- 8. Диаметр молекулы воды d=0,0000000003 м = 3 ∙ 10 -10 м 10 нулей
- 9. Масса атома водорода m = 0,0000000000000000000017 г Т.к. число 1
- 10. Масса атома водорода m = 0,0000000000000000000017 г = 21 нуль = 1,7 ∙ 10 -21 г
- 11. Масса планеты Венера М=4870000000000000000000000 кг
- 12. Масса планеты Венера М=4 870000000000000000000000 кг Отделяем первую цифру числа и ставим после неё запятую, число
- 13. Масса планеты Венера М=4 870000000000000000000000 кг = 24 цифры =4,87 ∙ 10 24 кг
- 14. Итак видим, что если число большое (>1), то показатель степени n положителен, а если число очень
- 15. Действия с числами в стандартном виде Запишем правила умножения и деления чисел в стандартном виде формулами:
- 16. Примеры умножения чисел в стандартном виде (4 ∙107) ∙ (2 ∙109)= 8 ∙ 107+9 = (8∙1012)
- 17. Примеры умножения чисел в стандартном виде (4 ∙107) ∙ (2 ∙109)= 8 ∙ 107+9 = 8
- 18. Примеры умножения чисел в стандартном виде (4 ∙107) ∙ (2 ∙109)= 8 ∙ 107+9 = 8
- 19. Примеры деления чисел в стандартном виде (9 ∙1012) : (2 ∙109)= 4,5 ∙1012-9 = (2 ∙1012)
- 20. Примеры деления чисел в стандартном виде (9 ∙1012) : (2 ∙109)= 4,5 ∙1012-9 = 4,5 ∙103
- 21. Примеры деления чисел в стандартном виде (9 ∙1012) : (2 ∙109)= 4,5 ∙1012-9 = 4,5 ∙103
- 23. Скачать презентацию

















 Показательная и логарифмическая функции. Показательные уравнения
Показательная и логарифмическая функции. Показательные уравнения Системы линейных уравнений с двумя переменными. 7 класс
Системы линейных уравнений с двумя переменными. 7 класс Геометрические задачи С2, по материалам ЕГЭ
Геометрические задачи С2, по материалам ЕГЭ Несобственные интегралы с бесконечными пределами
Несобственные интегралы с бесконечными пределами Углы. Виды углов и их построение. 5 класс
Углы. Виды углов и их построение. 5 класс Построение сечений многогранников
Построение сечений многогранников Сумма углов треугольника
Сумма углов треугольника Определение первообразной
Определение первообразной Правильные многогранники. Метапредмет – хаос и порядок
Правильные многогранники. Метапредмет – хаос и порядок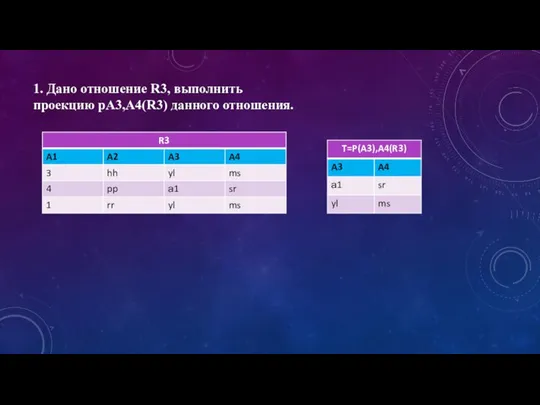 Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения
Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения Дисперсионный анализ ANOVA (продолжение). Занятие 4
Дисперсионный анализ ANOVA (продолжение). Занятие 4 Способы преобразования чертежа
Способы преобразования чертежа Формулы двойного аргумента. (Часть 1)
Формулы двойного аргумента. (Часть 1) Математика царица всех наук. Вперёд к приключениям
Математика царица всех наук. Вперёд к приключениям Теорема Пифагора
Теорема Пифагора Презентация по математике "Решение задач на разностное и кратное сравнение чисел" - скачать бесплатно
Презентация по математике "Решение задач на разностное и кратное сравнение чисел" - скачать бесплатно Алгоритмизация. Виды и свойства алгоритмов
Алгоритмизация. Виды и свойства алгоритмов Первообразные
Первообразные Современный урок. Математика
Современный урок. Математика Математика. Думать – коллективно!
Математика. Думать – коллективно! Теорема Фалеса
Теорема Фалеса Математика в спорте. Хоккей
Математика в спорте. Хоккей Упрощение выражений. Тест
Упрощение выражений. Тест Свойства степени с натуральным показателем. 9 класс
Свойства степени с натуральным показателем. 9 класс Факторный анализ
Факторный анализ Составление и решение задач разного типа различными способами Лоретц Анна Васильевна, Учитель начальных классов, МОУ «СОШ №
Составление и решение задач разного типа различными способами Лоретц Анна Васильевна, Учитель начальных классов, МОУ «СОШ № Конус
Конус Сложение и вычитание многочленов
Сложение и вычитание многочленов