Пусть f(x,y) – функция, ограниченная в некоторой замкнутой ограниченной
области D.
- частичная область области D. - площадь частичной области
значение функции в точке
Составим сумму (*)
Сумма (*) называется интегральной суммой для функции f(x,y) в области D,
соответствующей данному разбиению области D на n – частичных
областей.
Определение
Двойным интегралом от функции f(x,y) по области D называется предел, к
которому стремится интегральная сумма при стремлении к 0 наибольшего
диаметра частичных областей
Запись








 Игра "Поле чудес" геометрия
Игра "Поле чудес" геометрия Презентация по математике "Трансцендентная кривая. Спираль Архимеда" - скачать
Презентация по математике "Трансцендентная кривая. Спираль Архимеда" - скачать  Функция нескольких переменных
Функция нескольких переменных Преобразования графиков функций. 10 класс
Преобразования графиков функций. 10 класс Перевірка статистичних гіпотез
Перевірка статистичних гіпотез Геометрия моими глазами. Евклидова и неевклидова геометрия
Геометрия моими глазами. Евклидова и неевклидова геометрия Что лишнее?
Что лишнее? Письмове додавання трицифрових чисел, коли сума одиниць дорівнює 10 або сума десятків дорівнює 10 десяткам
Письмове додавання трицифрових чисел, коли сума одиниць дорівнює 10 або сума десятків дорівнює 10 десяткам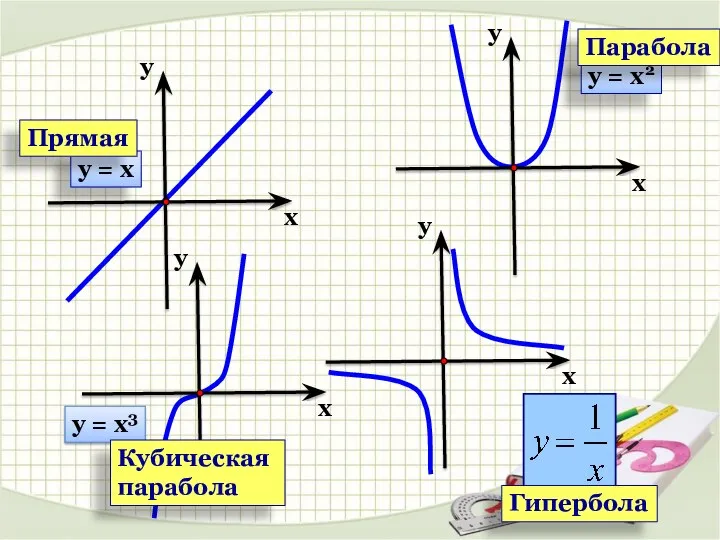 Степенная функция
Степенная функция Первый признак равенства треугольников
Первый признак равенства треугольников Логика предикатов
Логика предикатов Решение неравенств и систем неравенств. 8 класс
Решение неравенств и систем неравенств. 8 класс Математические задачи компьютерной томографии
Математические задачи компьютерной томографии Математическая модель ведения боевых действий с учетом сил авиации и ПВО
Математическая модель ведения боевых действий с учетом сил авиации и ПВО Координатная прямая Урок математики в 6 классе с использованием интерактивной доски Panasonic elite Panаboard book
Координатная прямая Урок математики в 6 классе с использованием интерактивной доски Panasonic elite Panаboard book  Аттестационная работа. Программа элективного курса Математические основы информатики
Аттестационная работа. Программа элективного курса Математические основы информатики Презентация Теория принятия решении в условиях неопределенности
Презентация Теория принятия решении в условиях неопределенности Расстояние между параллельными прямыми
Расстояние между параллельными прямыми Движение_в_противоположном_направлении
Движение_в_противоположном_направлении Корреляции. Регрессионный анализ
Корреляции. Регрессионный анализ Логарифмы. Определение логарифма
Логарифмы. Определение логарифма Системы линейных дифференциальных уравнений
Системы линейных дифференциальных уравнений Презентация по математике "Сажень" - скачать бесплатно
Презентация по математике "Сажень" - скачать бесплатно Квадратные уравнения
Квадратные уравнения Теория графов путь, цепь, цикл
Теория графов путь, цепь, цикл Презентация на тему Признаки параллельности прямых
Презентация на тему Признаки параллельности прямых  Тіла обертання. Циліндр
Тіла обертання. Циліндр Двойные интегралы
Двойные интегралы