Содержание
- 2. Конечные поля Теория конечных полей является центральной математической теорией, лежащей в основе помехоустойчивого кодирования и криптологии.
- 3. Определение Пусть F есть множество с двумя бинарными операциями + и *. F называется полем, если
- 4. Определение Если число элементов F конечно, то F называется конечным полем
- 5. Арифметика по модулю Обозначим: Zn = {0, 1, … , n-1} a mod n есть остаток
- 6. Теорема: (p – простое число) с операциями сложения и умножения целых чисел по модулю p есть
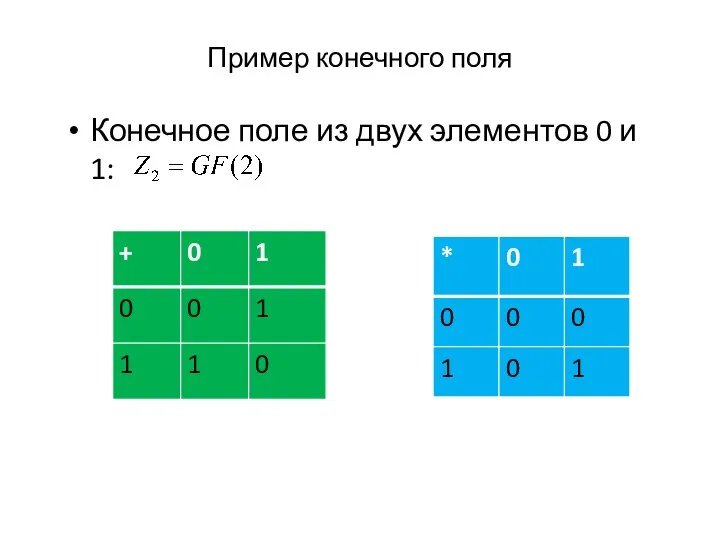
- 7. Пример конечного поля Конечное поле из двух элементов 0 и 1:
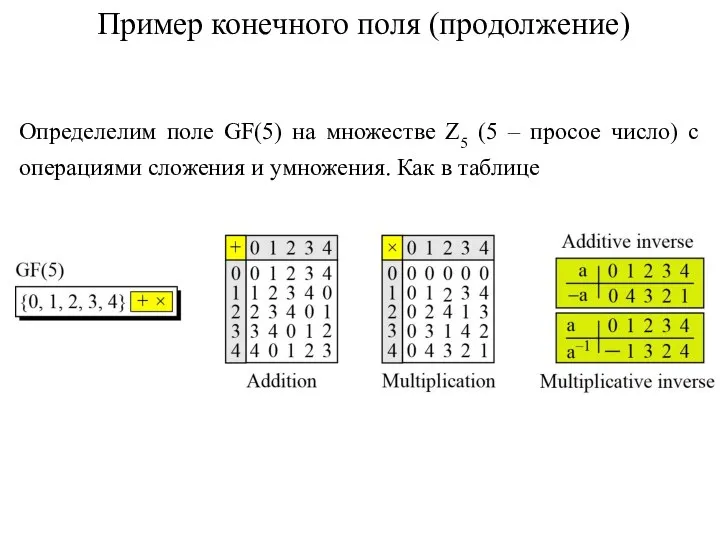
- 8. Пример конечного поля (продолжение) Определелим поле GF(5) на множестве Z5 (5 – просое число) с операциями
- 9. Циклические группы Определение: Элемент g конечной группы G называется порождающим или примитивным элементом, если все элементы
- 10. Определение Порядок группы G – число элементов группы (обозначение |G| ). Порядок элемента g є G
- 11. Теорема 1: является циклической только если n есть одно из чисел , где p есть нечетное
- 12. Теорема 4: Пусть G есть циклическая группа из n элементов и являются делителями n, тогда существуют
- 13. Конечные поля Эварист Галуа(1811 -1832)
- 14. Многочлены Многочлен степени n ai – коэффициенты из некоторого множества (поля)
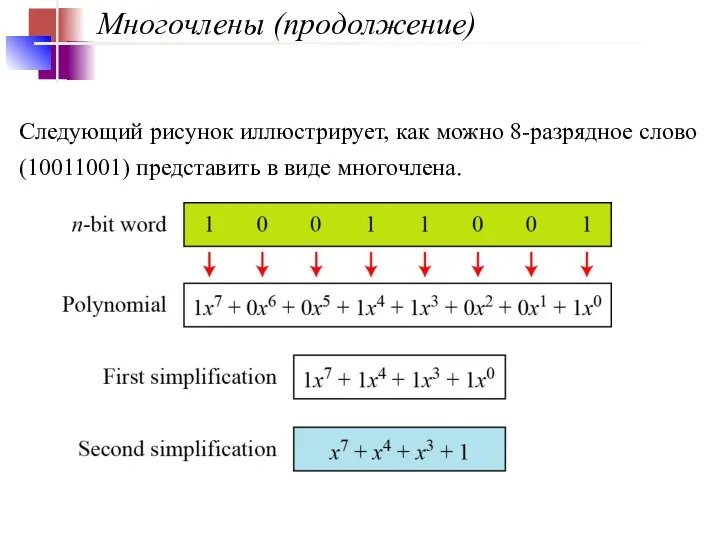
- 15. Многочлены (продолжение) Следующий рисунок иллюстрирует, как можно 8-разрядное слово (10011001) представить в виде многочлена.
- 16. Расширенные конечные поля Конечные поля существуют только для порядков q=pm (p – простое, m – натуральное).
- 17. Расширенные конечные поля Подобно этому расширенное поле GF(pm) порядка q=pm при m>1 можно ассоциировать с множеством
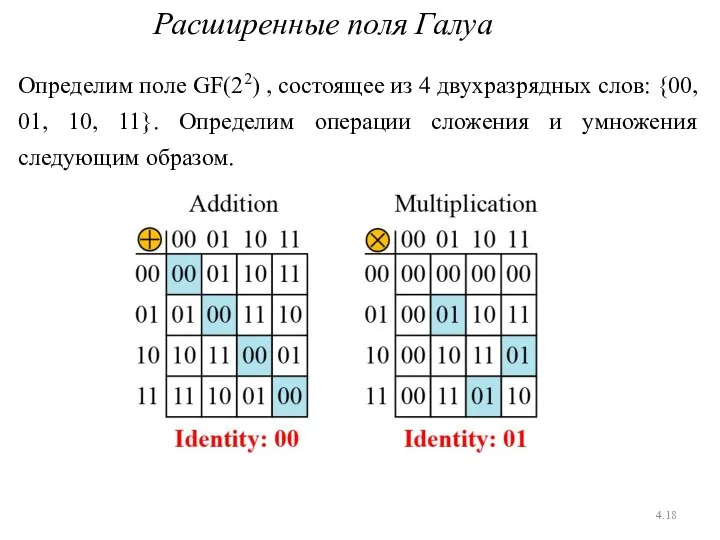
- 18. 4. Расширенные поля Галуа Определим поле GF(22) , состоящее из 4 двухразрядных слов: {00, 01, 10,
- 19. Многочлены - модули Для построения поля GF(2n) используются многочлены – модули над полем GF(2), которые должны
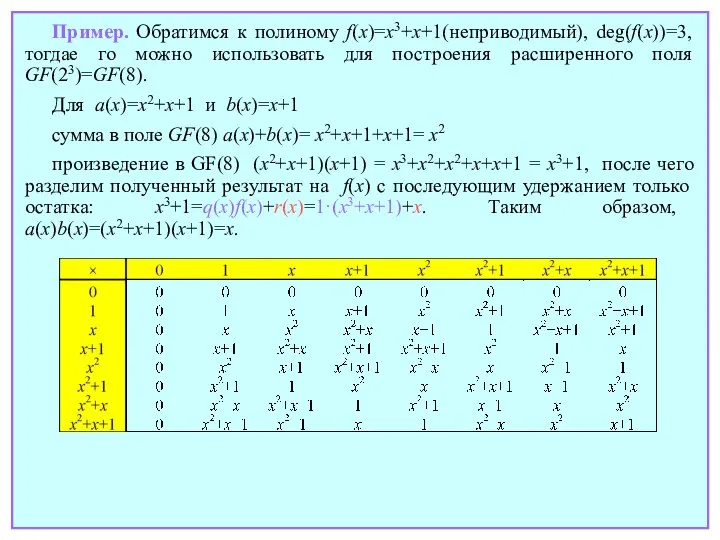
- 20. Пример. Обратимся к полиному f(x)=x3+x+1(неприводимый), deg(f(x))=3, тогдае го можно использовать для построения расширенного поля GF(23)=GF(8). Для
- 21. Мультипликативный порядок элементов поля. Примитивные элементы В любом поле GF(q), будь оно простым или расширенным, можно
- 22. Возьмем некоторый ненулевой элемент α∈GF(q) и рассмотрим его степени α1, α2, …, αl, … . Поскольку
- 23. Пример 1. Элемент 2 поля GF(7) имеет мультипликативный порядок t=3 поскольку для него 21=2, 22=4, 23=1.
- 24. Структура конечных полей Пусть f(x) – неприводимый многочлен степени n над полем F и α -
- 25. Структура конечных полей Пример: α корень многочлена 1+x+x3 над GF(2) , то есть 1+x+x3 GF(2)[x]. Следовательно,
- 26. Структура конечных полей Таблица логарифмов Zech: Пусть α – примитивный элемент GF(q). Для каждого 0≦i≦q-2 или
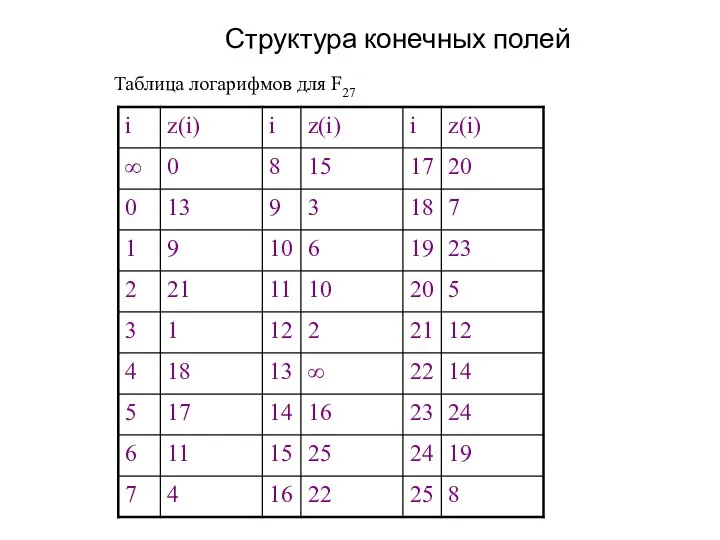
- 27. Структура конечных полей Таблица логарифмов для F27
- 28. Теорема: Произвольный неприводимы многочлен над полем GF(2) делит многочлен Xn+1, где n = 2m-1 и m
- 29. Примитивные многочлены Неприводимый многочлен p(X) степени m называется примитивным, если n – наименьшее положительное целое число
- 30. Пример. Элементы 3 и 5 поля GF(7) являются примитивными, тогда как остальные ненулевые элементы непримитивны. Действительно,
- 31. Построение расширенного поля GF(pm) в виде таблицы степеней примитивного элемента начинается с выбора примитивного полинома степени
- 32. Пример. Полином f(x)=x3+x+1 примитивен над GF(2). Учтя, что в GF(8) построенном с помощью f(x), x3= x+1
- 33. Некоторые свойства расширенных конечных полей Теорема 1. Среди всех элементов расширенного поля GF(2m) лишь элементы основного
- 34. Построение полиномов с заданными корнями Одно из фундаментальных положений классической алгебры утверждает, что любой полином f(x)
- 35. Пример 1. Рассмотрим полином g(z)=z3+z2+1. Легко убедиться, что у него нет корней в GF(2): g(1)= g(0)=1.
- 36. где все q–1 ненулевых элементов GF(q) выражены как степени примитивного элемента ς. Теорема 1. Пусть l
- 37. Алгоритмы Алгоритм Евклида нахождения НОД Расширенный алгоритм Евклида Возведение в степень
- 38. Векторное пространство(V,F, +, .) F - поле V множество элементов(векторов) Сложение векторов(коммутативное, ассоциат-е) Умножение на число
- 40. Скачать презентацию































 Обратная матрица. (Тема 7)
Обратная матрица. (Тема 7) Абсолютные и относительные показатели
Абсолютные и относительные показатели Функції багатьох змінних
Функції багатьох змінних Системы счисления. Арифметические действия над систематическими числами
Системы счисления. Арифметические действия над систематическими числами Независимая переменная имеет больше двух уровней
Независимая переменная имеет больше двух уровней Математика 5 класс Тема: Деление и дроби Учитель: Мифтахова Гелнур Фаритовна, СОШ №24 г.Набережные Челны 2010 год
Математика 5 класс Тема: Деление и дроби Учитель: Мифтахова Гелнур Фаритовна, СОШ №24 г.Набережные Челны 2010 год  Умножение круглых чисел
Умножение круглых чисел Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс Прямоугольный треугольник
Прямоугольный треугольник Понятия НОД и НОК,
Понятия НОД и НОК, Презентация по математике "Страна математических вычислений" - скачать
Презентация по математике "Страна математических вычислений" - скачать  Делимость чисел Презентация по математике
Делимость чисел Презентация по математике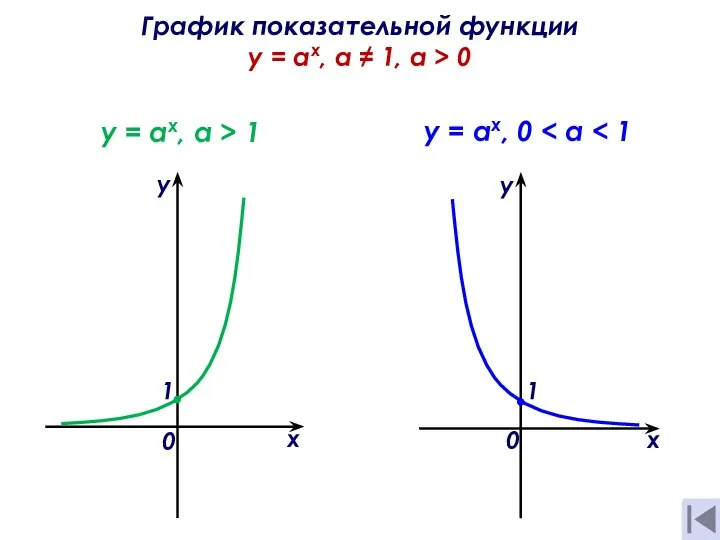 Показательные уравнения
Показательные уравнения Простые и сложные проценты. Составитель: учитель математики МОУ Кулуевская СОШ Ишбирдина Таслима Нуховна
Простые и сложные проценты. Составитель: учитель математики МОУ Кулуевская СОШ Ишбирдина Таслима Нуховна Презентация по математике "Аликвота" - скачать бесплатно
Презентация по математике "Аликвота" - скачать бесплатно Элементы теории множеств
Элементы теории множеств Нахождение целого по части
Нахождение целого по части Хронология. Счет времени
Хронология. Счет времени Проценты. Решение задач на проценты. 5 класс
Проценты. Решение задач на проценты. 5 класс Презентация по математике "Математическая формула прекрасного" - скачать
Презентация по математике "Математическая формула прекрасного" - скачать  Конические поверхности. Поверхности вращения
Конические поверхности. Поверхности вращения Линейная функция. Методическая разработка
Линейная функция. Методическая разработка Таблица умножения и ее секреты
Таблица умножения и ее секреты Симметрия – вокруг нас Геометрия
Симметрия – вокруг нас Геометрия  Деление многозначного числа на однозначное число
Деление многозначного числа на однозначное число Логарифмические спирали
Логарифмические спирали Презентация на тему Слежение и вычитание положительных и отрицательных чисел
Презентация на тему Слежение и вычитание положительных и отрицательных чисел  Теорема Фалеса
Теорема Фалеса