Содержание
- 2. Нарахування простих процентів Нехай на початкову суму (теперішня величина грошових коштів) PV нараховують річну процентну ставку
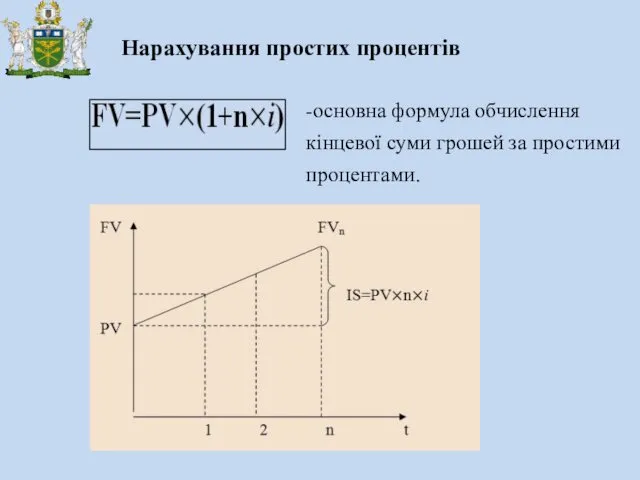
- 3. Нарахування простих процентів -основна формула обчислення кінцевої суми грошей за простими процентами.
- 4. Петро Клименко хоче дати в борг на один рік 1 млн. грн. під 9% річних. В
- 5. Приклад 1 (продовження) В кінці n-го року - Необхідно звернути увагу на слідуюче: - нарахування за
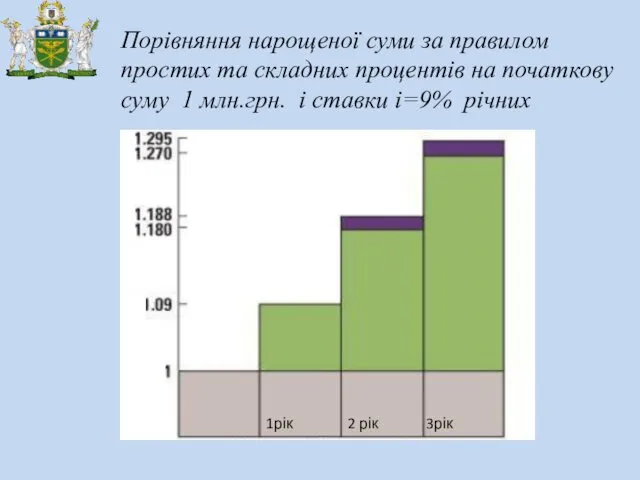
- 6. Порівняння нарощеної суми за правилом простих та складних процентів на початкову суму 1 млн.грн. і ставки
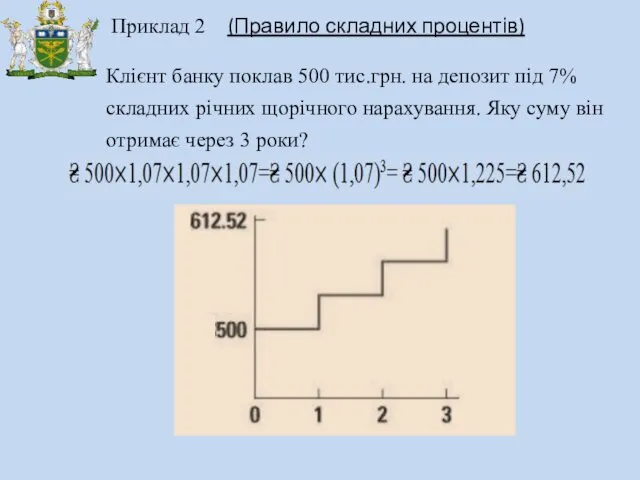
- 7. Клієнт банку поклав 500 тис.грн. на депозит під 7% складних річних щорічного нарахування. Яку суму він
- 8. Отже, в загальному вигляді нарощена сума буде змінюватись за правилом: формула нарощування за складними процентами множник
- 9. У випадку, якщо відсотки нараховуються m разів на рік, відсоток за період року складає де i-
- 10. Розглянемо випадок, коли кількість нарахувань необмеженно збільшується, тобто прямує до нескінченності (неперервне нарахування ) . Приймемо
- 11. Числова послідовність Позначення : x, y, z,.. – змінні; a, b, c,.. - сталі Означення 1.
- 12. Іншими словами: Числова послідовність - це функція натурального аргумента yn = f (n). Якщо із збільшенням
- 13. Означення 3. Число а називають границею числової послідовності хn , якщо для всякого наперед заданого як
- 14. Числова послідовність. Границя числової послідовності. Приклад 3. Показати, що змінна величина (числова послідовність) хn =2+1/1, x2=2+
- 15. Границя функції в точці.. Означення 3. Будемо розглядати функцію у =f (x ),визначену в деякому околі
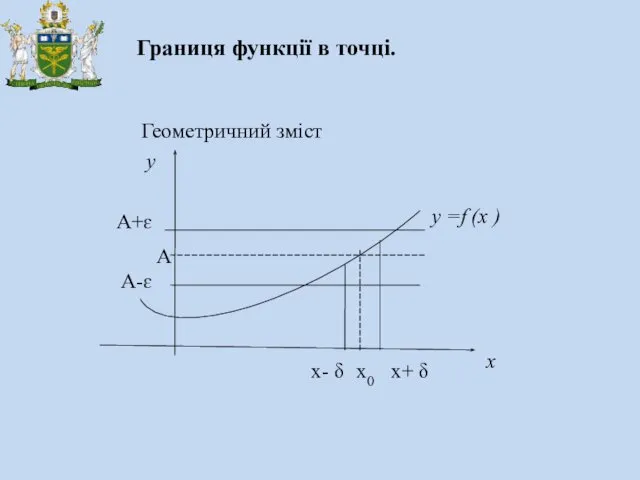
- 16. Границя функції в точці. Геометричний зміст y x A A+ɛ A-ɛ х0 х- δ х+ δ
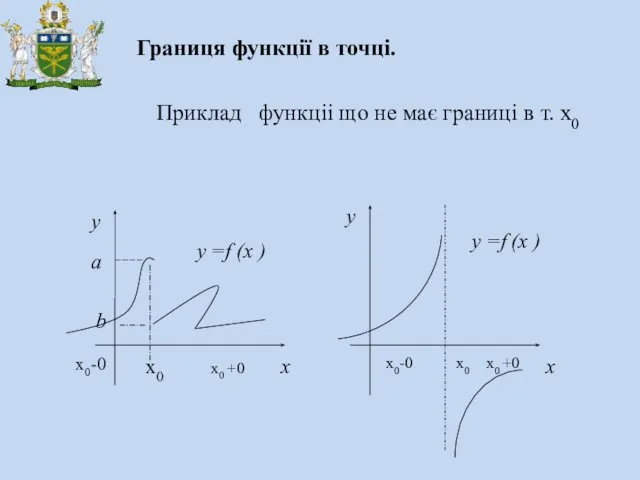
- 17. x0-0 x0 +0 Границя функції в точці. Приклад функціі що не має границі в т. х0
- 18. Односторонні границі. Означення 5 Якшо у =f (x ) прямує до границі А1, коли х прямує
- 19. Нескінченно малі величини. Означення 6. Функцію y =f (х) називають нескінченно малою коли х→х0 , або
- 21. Скачать презентацию













 Понятие логарифма
Понятие логарифма Несобственные интегралы
Несобственные интегралы Разные способы доказательства теоремы о сумме углов треугольника
Разные способы доказательства теоремы о сумме углов треугольника Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Тела вращения. Зачет
Тела вращения. Зачет Старинные меры длины
Старинные меры длины Эйлеровы графы. Гамильтоновы графы
Эйлеровы графы. Гамильтоновы графы Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел Презентация по математике "Построение циркулем и линейкой" - скачать бесплатно
Презентация по математике "Построение циркулем и линейкой" - скачать бесплатно Бір факторлы және екі факторлы дисперсиялық талдау
Бір факторлы және екі факторлы дисперсиялық талдау Платоновы тела. Правильные выпуклые многогранники
Платоновы тела. Правильные выпуклые многогранники Треугольники и их виды. Практическая работа № 1
Треугольники и их виды. Практическая работа № 1 Интерполирование и численное дифференцирование функций
Интерполирование и численное дифференцирование функций Геометрія. Многогранники
Геометрія. Многогранники Реализация концепции развития математического образования и проект “Математическая вертикаль”
Реализация концепции развития математического образования и проект “Математическая вертикаль” Линейная функция. Урок 35
Линейная функция. Урок 35 Длина ломаной
Длина ломаной Логическое следствие и метод резолюций. (Глава 3)
Логическое следствие и метод резолюций. (Глава 3) Разложение многочлена на множители способом группировки. 7 класс
Разложение многочлена на множители способом группировки. 7 класс Функции и их графики
Функции и их графики Взаимно простые числа. Признак делимости
Взаимно простые числа. Признак делимости Презентация на тему Блочно модульная технология
Презентация на тему Блочно модульная технология  Параллельность прямой и плоскости. Решение задач
Параллельность прямой и плоскости. Решение задач Многочлени. Узагальнення знання учнів
Многочлени. Узагальнення знання учнів Уравнение прямой
Уравнение прямой Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Матрицы. Определители. Их свойства. Системы линейных уравнений с неизвестными. Однородные системы линейных уравнений
Матрицы. Определители. Их свойства. Системы линейных уравнений с неизвестными. Однородные системы линейных уравнений Из истории десятичных дробей
Из истории десятичных дробей