Содержание
- 2. Отношения «равно», «меньше», «больше»
- 3. Аксиоматический подход Число а равно числу b (а = b), если они непосредственно следуют за одним
- 4. Пусть А и В – конечные множества, n(А) = а, n(В) = b, т. е. а
- 5. - Множества А и В содержат поровну элементов, т. е. А и В равночисленны - Множества
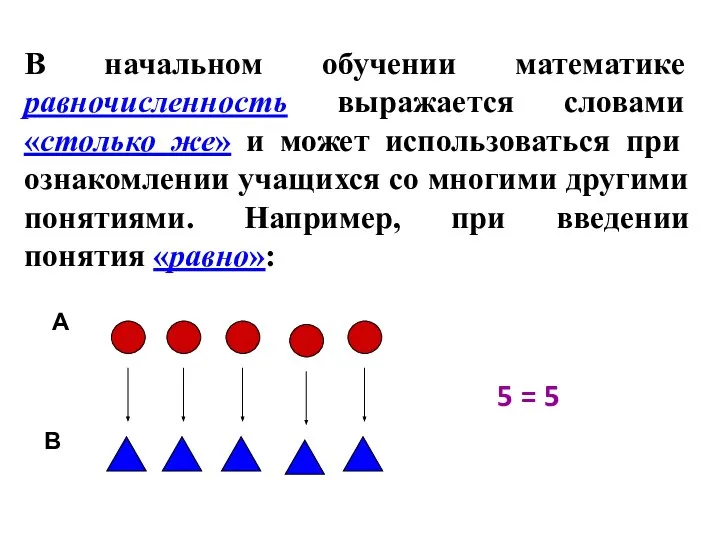
- 6. В начальном обучении математике равночисленность выражается словами «столько же» и может использоваться при ознакомлении учащихся со
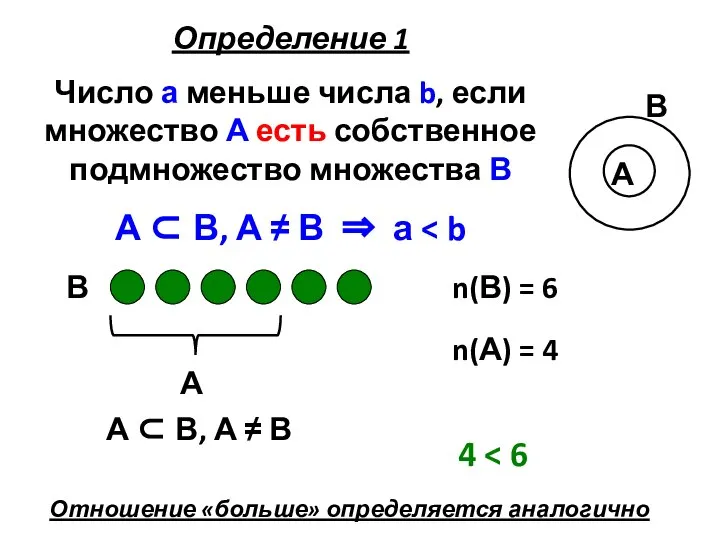
- 7. Определение 1 Число а меньше числа b, если множество А есть собственное подмножество множества В А
- 8. Пример: используя теоретико-множественный подход к понятию числа, покажите, что 3 А = {а, b, c}, n(A)
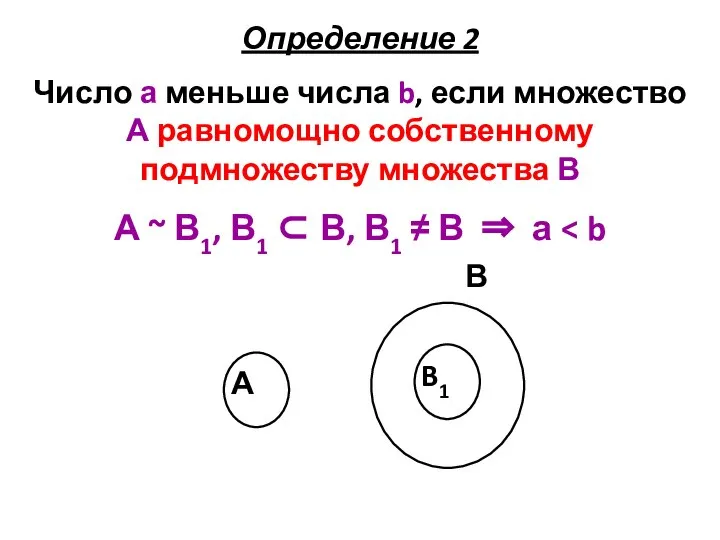
- 9. Определение 2 Число а меньше числа b, если множество А равномощно собственному подмножеству множества В А
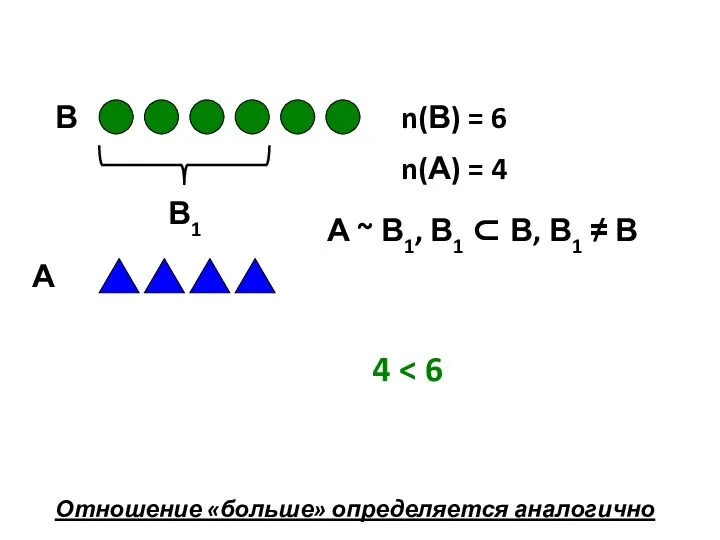
- 10. 4 Отношение «больше» определяется аналогично
- 11. Пример: используя теоретико-множественный подход к понятию числа, покажите, что 3 А = {а, b, c}, n(A)
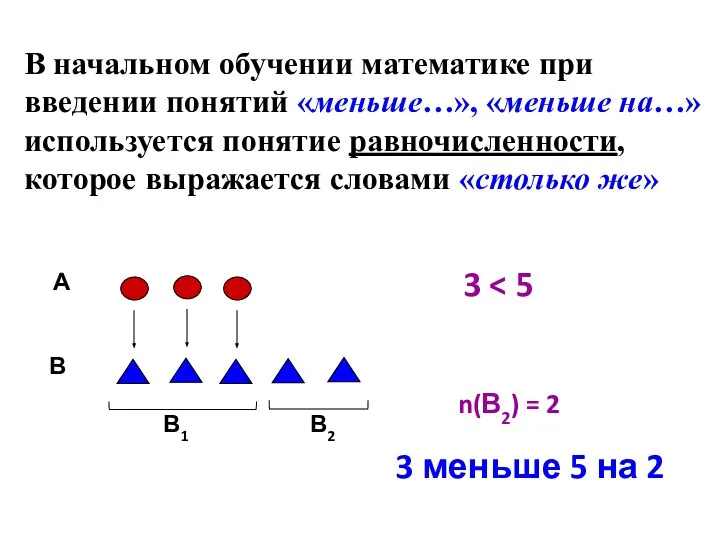
- 12. В начальном обучении математике при введении понятий «меньше…», «меньше на…» используется понятие равночисленности, которое выражается словами
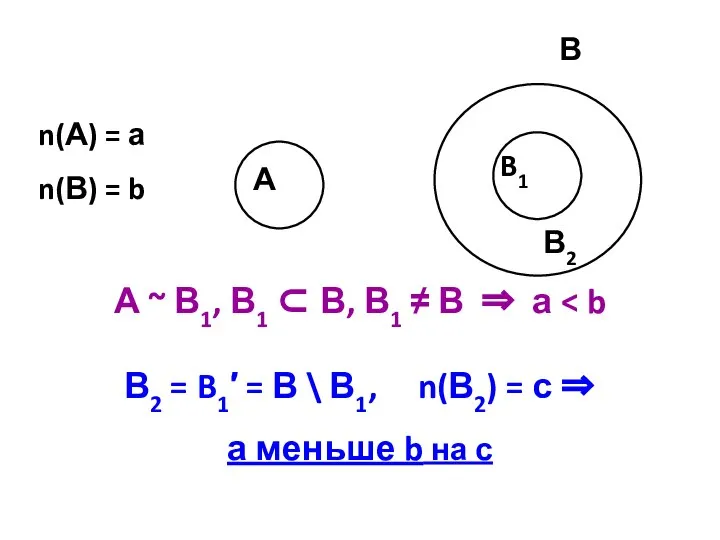
- 13. А ~ В1, В1 ⊂ В, В1 ≠ В ⇒ а В2 = B1′ = В
- 14. Если длины отрезков а и b выражаются натуральными числами р и q (при одной и той
- 15. Свойства отношения равно рефлексивность: а = а 2) симметричность: а = b ⇒ b = а
- 16. Свойства отношения «меньше» 2) Транзитивность: а Отношение «меньше» на множестве N является отношением порядка, так как
- 17. Для любых натуральных чисел а, b и с верно только одно из следующих отношений: а =
- 18. Свойства множества натуральных чисел 1) Бесконечность (А 2) 2) Упорядоченность (отношения «меньше», больше») 3) Во множестве
- 20. а = b, если а и b непосредственно следуют за одним и тем же числом n
- 22. Скачать презентацию













 Иррациональные уравнения
Иррациональные уравнения Смежные углы
Смежные углы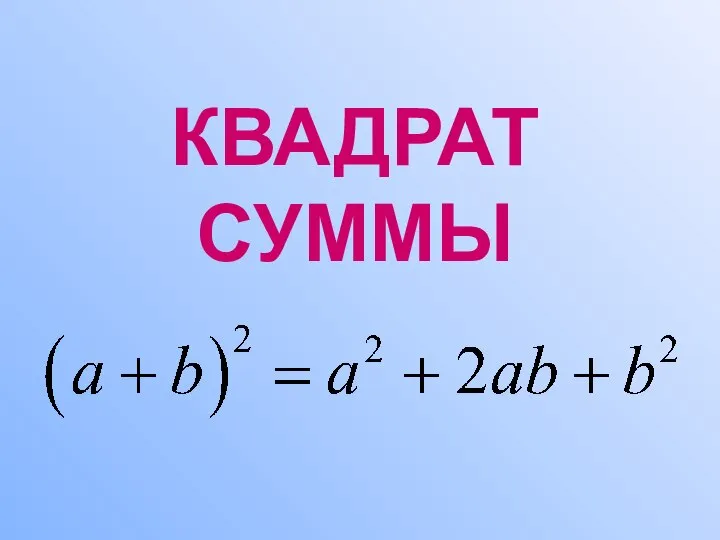 Квадрат суммы
Квадрат суммы Подготовительный этап к изучению нумерации в программе Дорофеева Г.В
Подготовительный этап к изучению нумерации в программе Дорофеева Г.В Построение правильных многоугольников
Построение правильных многоугольников Задания по математике (5 класс, часть 6)
Задания по математике (5 класс, часть 6) Логические высказывания
Логические высказывания Математика. 4 класс
Математика. 4 класс Геометрические фигуры. Игра
Геометрические фигуры. Игра Сложение и вычитание смешанных чисел (урок математики в 6 классе)
Сложение и вычитание смешанных чисел (урок математики в 6 классе) Геометрические миниатюры
Геометрические миниатюры Мир чисел
Мир чисел Презентация по математике "Решение текстовых задач арифметическим способом с помощью смешанных дробей" - скачать
Презентация по математике "Решение текстовых задач арифметическим способом с помощью смешанных дробей" - скачать  Синус, косинус, тангенс острого угла прямоугольного треугольника
Синус, косинус, тангенс острого угла прямоугольного треугольника Признаки равенства треугольников
Признаки равенства треугольников Композиция функций (сложная функция)
Композиция функций (сложная функция) Иностранные меры длины
Иностранные меры длины Нелинейная динамика. Лекция 4
Нелинейная динамика. Лекция 4 Матрицы и определители. (Лекция 1)
Матрицы и определители. (Лекция 1) Относительная частота случайного события
Относительная частота случайного события Правила математических знаков
Правила математических знаков Многогранники. Гимнастика ума
Многогранники. Гимнастика ума Масштаб и его виды
Масштаб и его виды Треугольники. Высота, медиана, биссектриса треугольника
Треугольники. Высота, медиана, биссектриса треугольника Творческая работа «Ремонт комнаты». Сделать верные расчёты
Творческая работа «Ремонт комнаты». Сделать верные расчёты Development of an information system for evaluating the work of production employees based on statistical analysis
Development of an information system for evaluating the work of production employees based on statistical analysis Построение сечений многогранников
Построение сечений многогранников 6 класс
6 класс