Содержание
- 2. Определение числовой функции Тригонометрические функции Обратные тригонометрические функции ОГЛАВЛЕНИЕ
- 3. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Тригонометрические функции Числовая окружность Синус и косинус Тангенс и котангенс Тригонометрические функции числового аргумента
- 4. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Обратные тригонометрические функции Функция y = arcsin x Свойства функции y = arcsin
- 5. ОПРЕДЕЛЕНИЕ ЧИСЛОВОЙ ФУНКЦИИ Определение 1. Если даны числовое множество X и правило f, позволяющее поставить в
- 6. Задача тригонометрии. Определение сторон и углов треугольника, когда уже известны некоторые из них. Определение. Тригонометрические функции
- 7. Определение. Числовая окружность – единичная окружность с установленным соответствием (между действительными числами и точками окружности). Уравнение
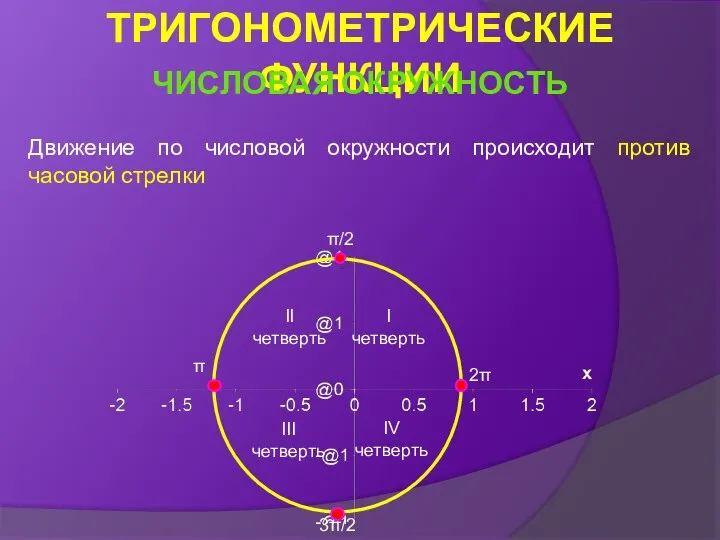
- 8. Движение по числовой окружности происходит против часовой стрелки π/2 π 3π/2 2π I четверть II четверть
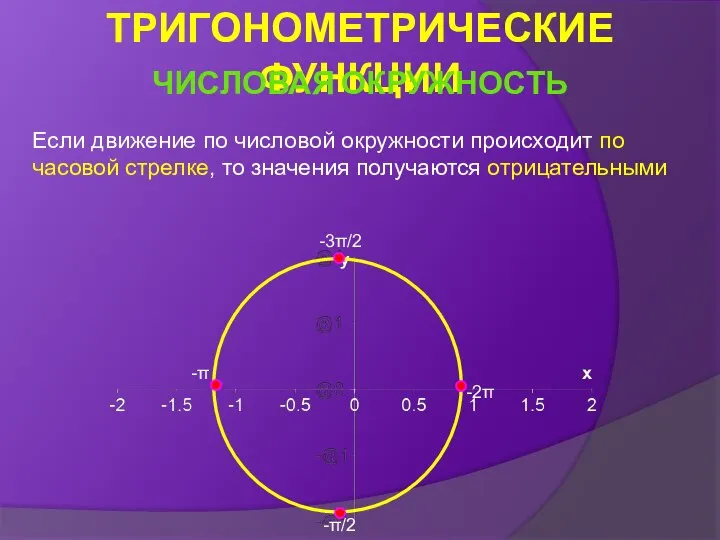
- 9. Если движение по числовой окружности происходит по часовой стрелке, то значения получаются отрицательными -π/2 -π -3π/2
- 10. Если точка М числовой окружности соответствует числу t, то она соответствует и числу вида t +
- 11. Определение. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа
- 12. Свойство 1. Для любого числа t справедливы равенства: Свойство 2. Для любого числа t справедливы равенства:
- 13. Определение. Отношение синуса числа t к косинусу того же числа называют тангенсом числа t и обозначают
- 14. Свойство 1. Для любого допустимого значения t справедливы равенства: Свойство 2. Для любого допустимого значения t
- 15. Определение. Тригонометрические функции числового аргумента t – функции y = sin t, y = cos t,
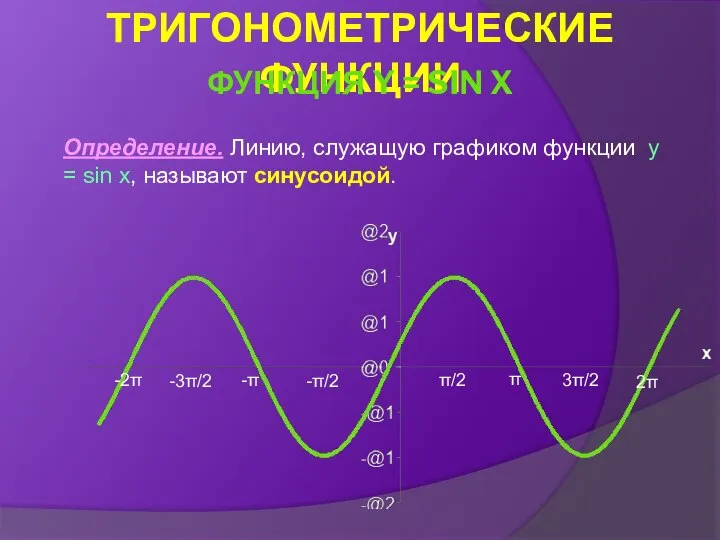
- 16. Определение. Линию, служащую графиком функции y = sin x, называют синусоидой. 2π -π π -2π -3π/2
- 17. СВОЙСТВА ФУНКЦИИ Y = SIN X. Свойство 1. D(y) = (-∞;+∞). Свойство 2. E(y) = [-1;1].
- 18. СВОЙСТВА ФУНКЦИИ Y = SIN X. Свойство 6. Функция y = sin x периодическая, ее основной
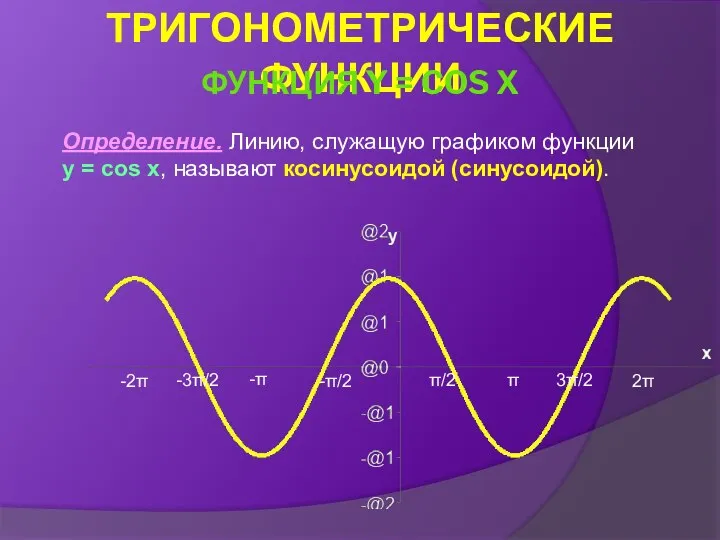
- 19. Определение. Линию, служащую графиком функции y = cos x, называют косинусоидой (синусоидой). -π/2 -3π/2 3π/2 π/2
- 20. СВОЙСТВА ФУНКЦИИ Y = COS X. Свойство 1. D(y) = (-∞;+∞). Свойство 2. E(y) = [-1;
- 21. СВОЙСТВА ФУНКЦИИ Y = COS X. Свойство 6. Функция y = cos x периодическая, ее основной
- 22. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ФУНКЦИЯ Y = TG X Определение. Линию, служащую графиком функции y = tg x
- 23. СВОЙСТВА ФУНКЦИИ Y = TG X. Свойство 1. D(y) = множество всех действительных чисел, за исключением
- 24. СВОЙСТВА ФУНКЦИИ Y = TG X. Свойство 5. Функция y = tg x возрастает на любом
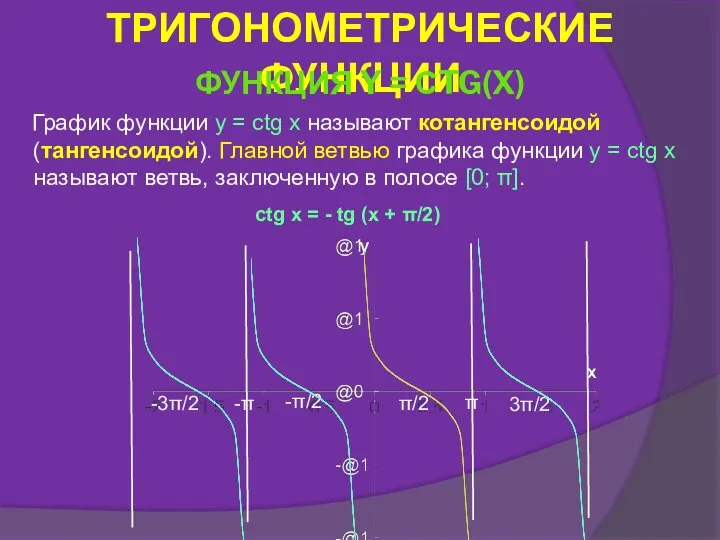
- 25. График функции y = ctg x называют котангенсоидой (тангенсоидой). Главной ветвью графика функции y = ctg
- 26. СВОЙСТВА ФУНКЦИИ Y = CTG X. Свойство 1. D(y) = множество всех действительных чисел, за исключением
- 27. СВОЙСТВА ФУНКЦИИ Y = CTG X. Свойство 5. Функция y = сtg x убывает на любом
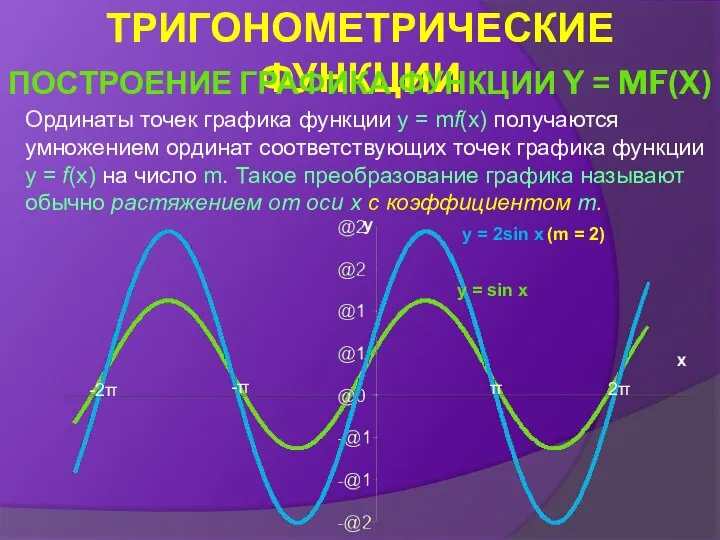
- 28. Ординаты точек графика функции y = mf(x) получаются умножением ординат соответствующих точек графика функции y =
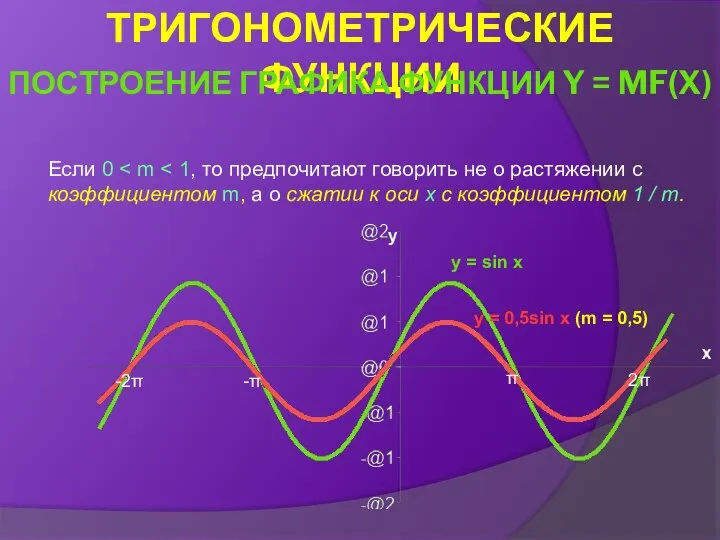
- 29. Если 0 y = sin x y = 0,5sin x (m = 0,5) -2π -π π
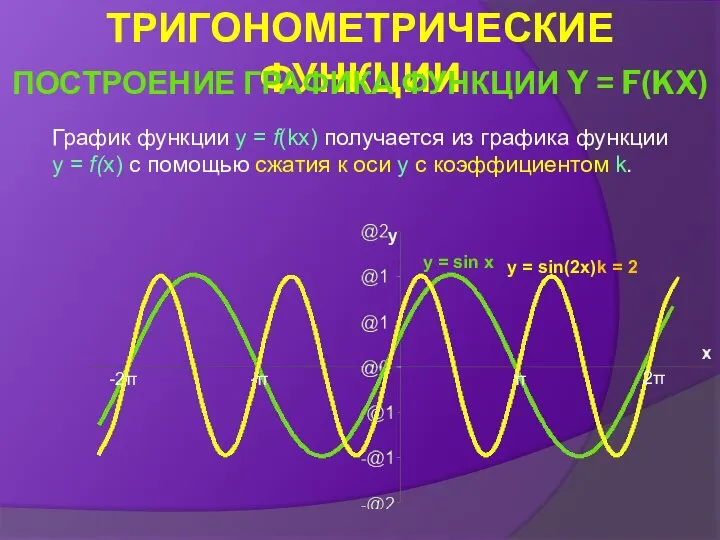
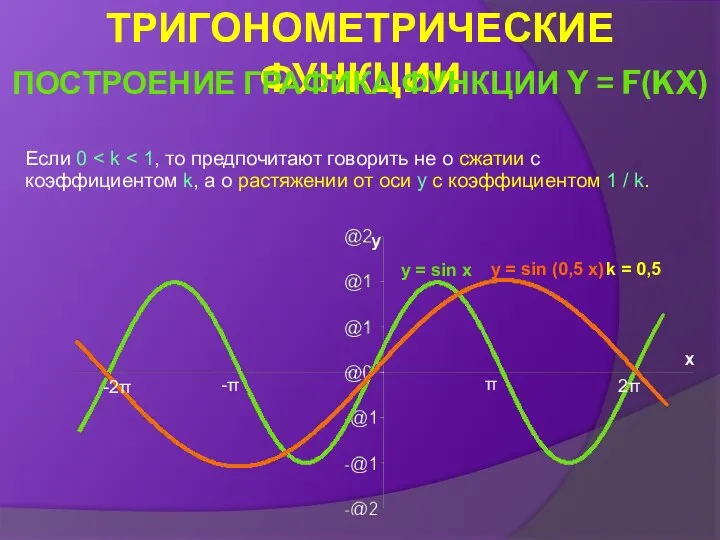
- 30. График функции y = f(kx) получается из графика функции y = f(x) с помощью сжатия к
- 31. Если 0 y = sin x y = sin (0,5 x) k = 0,5 -2π -π
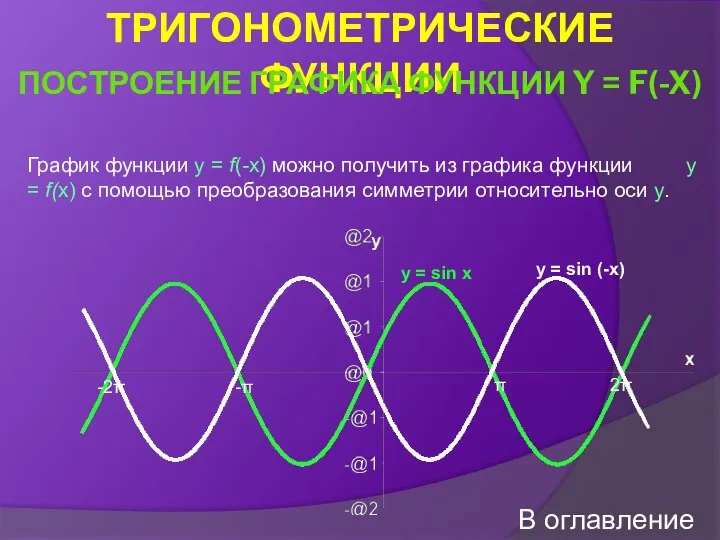
- 32. График функции y = f(-x) можно получить из графика функции y = f(x) с помощью преобразования
- 33. Закон (уравнение) гармонических колебаний: s – отклонение материальной точки от положения равновесия A (или – А,
- 34. Рассмотрим пример s = 3 sin (2t + π/3), где амплитуда равна трем (А = 3),
- 35. Дадим параметру k два соседних значения 0 и 1. При k = 0 получаем: t1 =
- 36. Найдем значение заданной функции в точке π/12: Точка C(π/12; 3) – верхняя точка искомой полуволны. ТРИГОНОМЕТРИЧЕСКИЕ
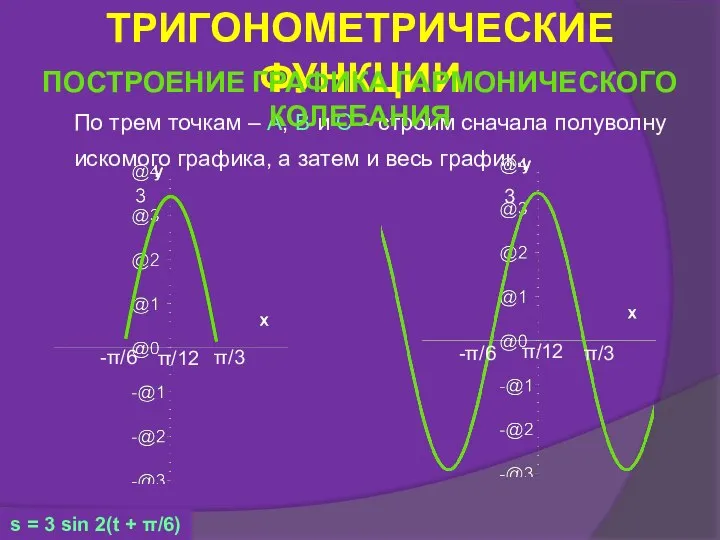
- 37. По трем точкам – A, B и C – строим сначала полуволну искомого графика, а затем
- 38. Определение. Обратными тригонометрическими функциями (или аркфункциями) называют функции вида y = arcsin x, y = arccos
- 39. Определение. y = arcsin x (читают: арксинус x) – это функция, обратная к функции y =
- 40. СВОЙСТВА ФУНКЦИИ Y = ARCSIN X. Свойство 1. D(f) = [-1;1]. Свойство 2. E(f) = [-π/2;
- 41. Определение. Если |a| ≤ 1, то arcsin a – это такое число из отрезка [-π/2; π/2],
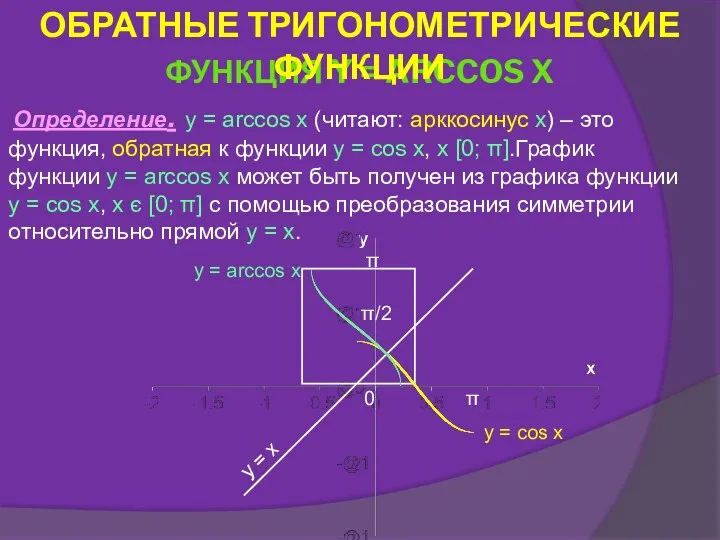
- 42. Определение. y = arccos x (читают: арккосинус x) – это функция, обратная к функции y =
- 43. СВОЙСТВА ФУНКЦИИ Y = ARCCOS X. Свойство 1. D(f) = [-1;1]. Свойство 2. E(f) = [0;
- 44. Определение. Если |a| ≤ 1, то arccos a – это такое число из отрезка [0; π],
- 45. Теорема. Для любого a є [-1; 1] выполняется равенство arccos a + arccos (-a) = π.
- 46. Определение. y = arctg x ( читают: арктангенс x) – это функция, обратная к функции y
- 47. СВОЙСТВА ФУНКЦИИ Y = ARCTG X. Свойство 1. D(f) = (-∞; +∞). Свойство 2. E(f) =
- 48. Определение. arctgs a – это такое число из интервала (-π/2; π/2), тангенс которого равен а. ОБРАТНЫЕ
- 49. Определение. y = arcctg x ( читают: арккотангенс x) – это функция, обратная к функции y
- 50. СВОЙСТВА ФУНКЦИИ Y = ARCCTG X. Свойство 1. D(f) = (-∞; +∞). Свойство 2. E(f) =
- 51. Определение. arcсtgs a – это такое число из интервала (0; π), котангенс которого равен а. ОБРАТНЫЕ
- 52. Наиболее важные соотношения для обратных тригонометрических функций: ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
- 54. Скачать презентацию



























![СВОЙСТВА ФУНКЦИИ Y = ARCSIN X. Свойство 1. D(f) = [-1;1].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/629905/slide-39.jpg)

![СВОЙСТВА ФУНКЦИИ Y = ARCCOS X. Свойство 1. D(f) = [-1;1].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/629905/slide-42.jpg)

![Теорема. Для любого a є [-1; 1] выполняется равенство arccos a](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/629905/slide-44.jpg)







 Нелинейная регрессия
Нелинейная регрессия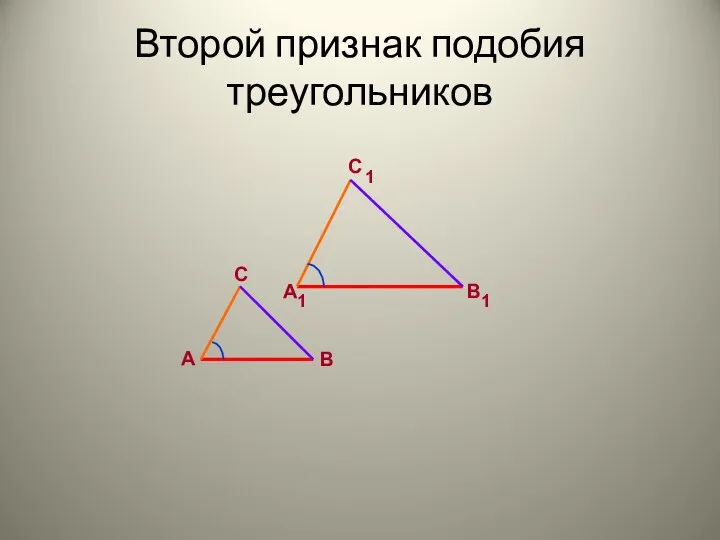 Второй признак подобия треугольников
Второй признак подобия треугольников Решаем выражения
Решаем выражения Объем конуса
Объем конуса Разложение многочлена на множители способом группировки
Разложение многочлена на множители способом группировки Генеральная совокупность и частотное распределение. Измерение связи между качественными переменными
Генеральная совокупность и частотное распределение. Измерение связи между качественными переменными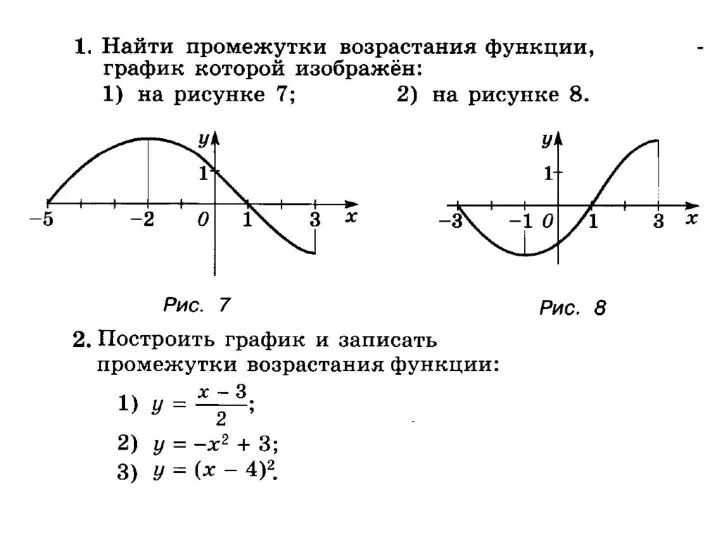 Четность и нечетность функции
Четность и нечетность функции Расстояние между точками координатной прямой
Расстояние между точками координатной прямой Функции нескольких переменных
Функции нескольких переменных Первый урок математики в 5 классе
Первый урок математики в 5 классе Нахождение дроби от числа
Нахождение дроби от числа МПМ-матрица посадочных лист
МПМ-матрица посадочных лист Количественные характеристики случайной величины. Описательная статистика. (Лекция 4)
Количественные характеристики случайной величины. Описательная статистика. (Лекция 4) Вправи на засвоєння таблиці додавання і віднімання числа 7
Вправи на засвоєння таблиці додавання і віднімання числа 7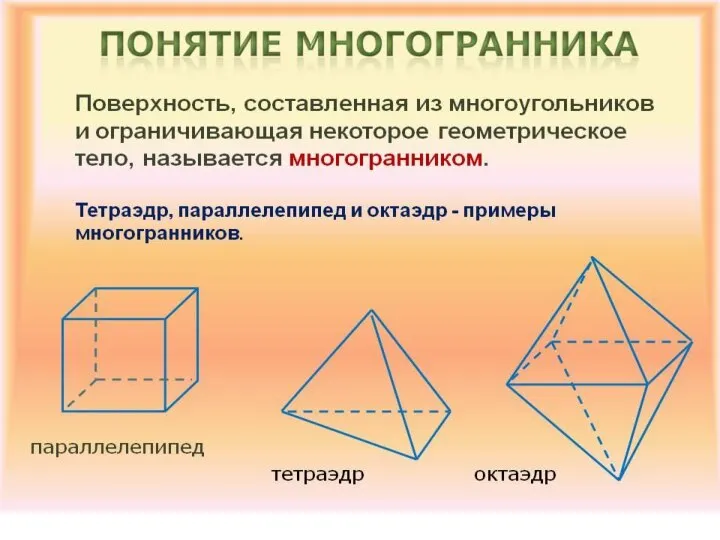 Понятие многогранника
Понятие многогранника Математическая логика_сокращ
Математическая логика_сокращ Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников ВКОШП-2011. Разбор задач
ВКОШП-2011. Разбор задач Комбинаторика. Комбинаторные конструкции
Комбинаторика. Комбинаторные конструкции Правила сложения и умножения в комбинаторике
Правила сложения и умножения в комбинаторике Линейная функция и её график
Линейная функция и её график Исследовательская работа Арифметика Л.Ф. Магницкого – «врата учёности» М.В. Ломоносова Работу выполнила: ученица 10«Б» класса
Исследовательская работа Арифметика Л.Ф. Магницкого – «врата учёности» М.В. Ломоносова Работу выполнила: ученица 10«Б» класса  Проценты. В здоровом теле – здоровый ум. 5 класс
Проценты. В здоровом теле – здоровый ум. 5 класс Тригонометрия в окружающем нас мире и в жизни человека
Тригонометрия в окружающем нас мире и в жизни человека Теорема Виета. Квадратные уравнения
Теорема Виета. Квадратные уравнения ОГЭ 2018. Модуль «Геометрия»
ОГЭ 2018. Модуль «Геометрия»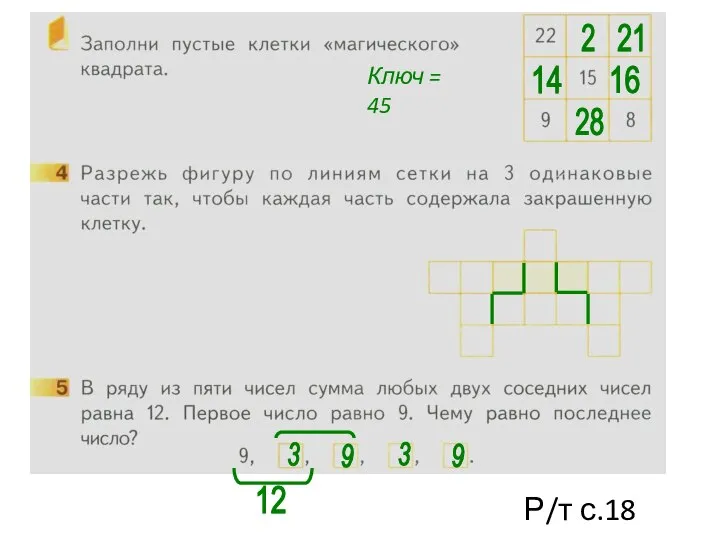 Помогайка
Помогайка Обыкновенные дроби
Обыкновенные дроби