Содержание
- 2. Трехмерная область Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью G. Пусть в области
- 3. Составление интегральных сумм Разобьём эту область V произвольным образом на элементарные ячейки с объёмами (i=1, 2,
- 4. Определение Назовём диаметром области максимальное расстояние между двумя точками области, лежащими на границе. Устремим максимальный диаметр
- 5. Определение Если существует конечный предел интегральных сумм при условии, что максимальный диаметр ячеек стремится к нулю,
- 6. Правильная трехмерная область Пусть пространственная область V, ограниченная замкнутой поверхностью G, удовлетворяет условиям: 1) всякая прямая,
- 7. Вычисление тройного интеграла Если область имеет вид как на рисунке, то тройной интеграл по такой области
- 8. Вычисление тройного интеграла Пример 1. Вычислить где V ограничена плоскостями x=0, y=0, z=0.
- 9. Решение.
- 11. Тройной интеграл в цилиндрических координатах При переходе от декартовых координат к цилиндрическим по формулам x=rcosφ, y=rsinφ,
- 12. Объем тела В декартовых координатах объем тела равен
- 13. Объем тела Общая формула для вычисления объема (независимо от системы координат) имеет вид
- 14. Объем тела Объём пространственной области V в цилиндрических координатах
- 15. Найти объем тела Вычислить объём тела, ограниченного поверхностями
- 16. Решение Найдём линию пересечения плоскостей, ограничивающих тело сверху и снизу. Очевидно, это y=1.
- 18. Найти объем тела Вычислить объём тела, ограниченного сферой и параболоидом (внутри параболоида).
- 19. Решение Вычислим объём тела, переходя к цилиндрическим координатам. Для этого запишем уравнения поверхностей в цилиндрических координатах:
- 20. Подставляя z= в одно из уравнений системы, получим
- 22. Скачать презентацию







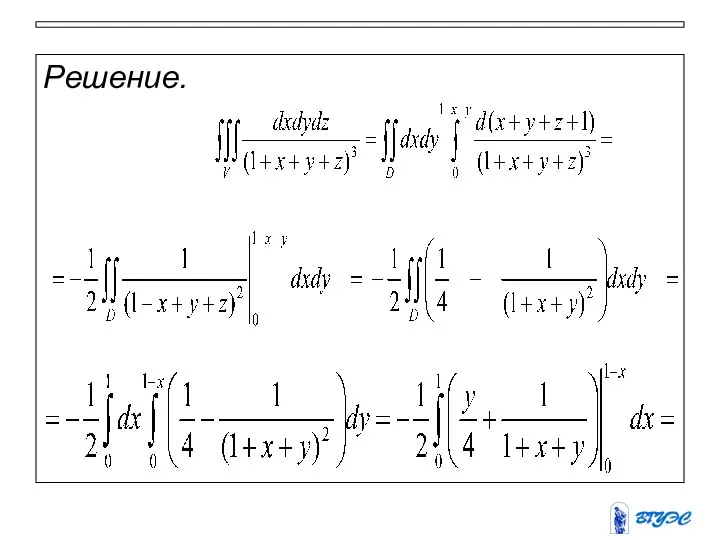





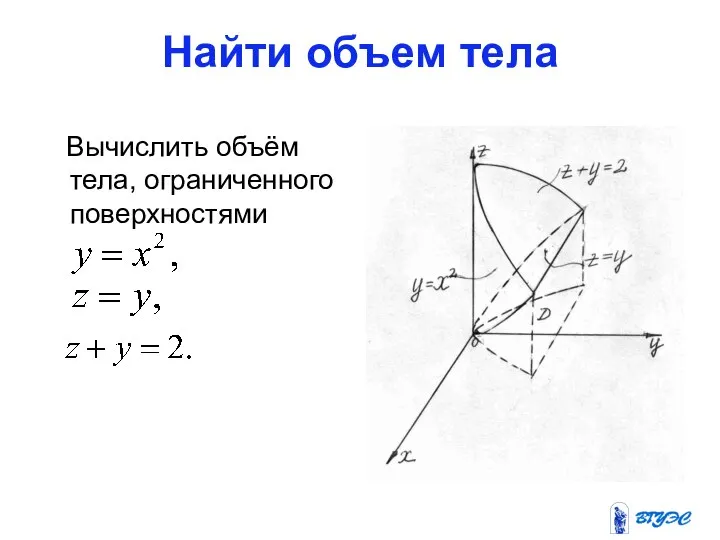


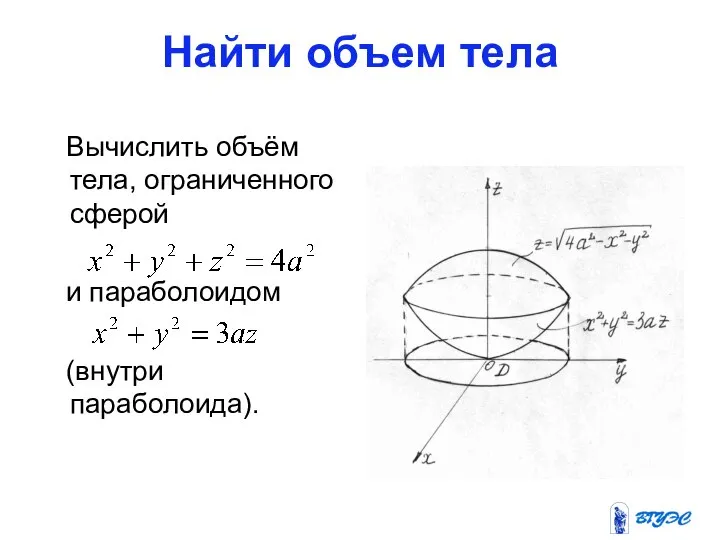


 График функции
График функции Числовая окружность
Числовая окружность Проценты. Скидки
Проценты. Скидки Случаи сложения и вычитания, основанные на знании нумерации чисел. 1 класс
Случаи сложения и вычитания, основанные на знании нумерации чисел. 1 класс Полигоны частот. Урок 1
Полигоны частот. Урок 1 Комбинаторная задача с лампочками
Комбинаторная задача с лампочками Последовательности
Последовательности Внутренний угол треугольника. Теорема о внешнем угле треугольника. Сумма углов треугольника
Внутренний угол треугольника. Теорема о внешнем угле треугольника. Сумма углов треугольника Точка. Задачи по геометрии №1-10
Точка. Задачи по геометрии №1-10 Высшая математика (практика)
Высшая математика (практика) Аттестационная работа. Математическое моделирование производственных процессов
Аттестационная работа. Математическое моделирование производственных процессов Презентация по математике "Учебные материалы" - скачать
Презентация по математике "Учебные материалы" - скачать  Есептеулер
Есептеулер Координатная прямая
Координатная прямая Конус. Усеченный конус. Основные понятия
Конус. Усеченный конус. Основные понятия Великие математики
Великие математики Презентация по математике "Число 10" - скачать бесплатно
Презентация по математике "Число 10" - скачать бесплатно Решение заданий ГИА. Модуль Геометрия
Решение заданий ГИА. Модуль Геометрия Введение понятия целого и дробного выражения
Введение понятия целого и дробного выражения Решение уравнений. 6 класс
Решение уравнений. 6 класс Введение в геометрию. 7 класс
Введение в геометрию. 7 класс Турнир юных математиков (5 класс)
Турнир юных математиков (5 класс) Проекция жазықтарын алмастыру әдісі
Проекция жазықтарын алмастыру әдісі Построение сечений тетраэдра. Решение задач
Построение сечений тетраэдра. Решение задач Презентация по математике "Даты и судьбы" - скачать
Презентация по математике "Даты и судьбы" - скачать  Презентация по математике "Первый признак равенства треугольников" - скачать бесплатно_
Презентация по математике "Первый признак равенства треугольников" - скачать бесплатно_ Правовая статистика
Правовая статистика Прямая и обратная пропорциональность. 6 класс
Прямая и обратная пропорциональность. 6 класс