Содержание
- 2. Цель урока: научиться применять таблицу производных при исследовании функций и построении графиков
- 3. Математический диктант Вариант 1. (Cu)’=… …=(u’v-v’u)/v² (cos x)’=… …=1/cos² x (ex)’=… Вариант 2. C’=… …=(u’v+v’u) (sin
- 4. Классная работа Одной из основных задач, возникающих при исследовании функции, является нахождение промежутков монотонности функции (промежутков
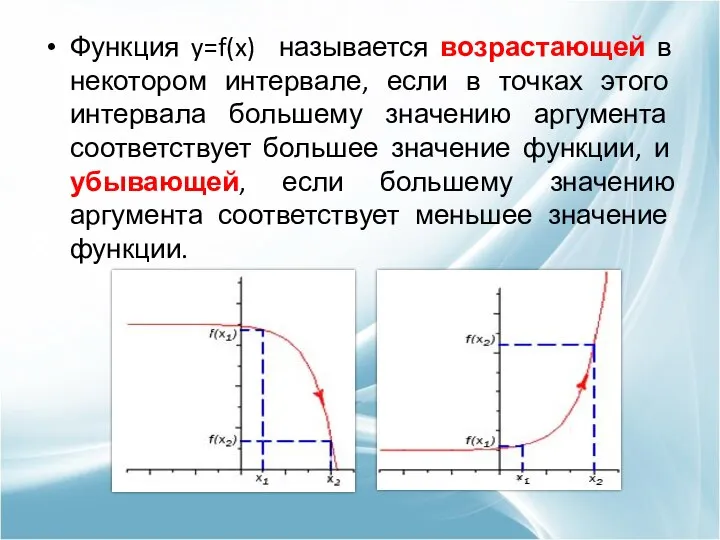
- 5. Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует
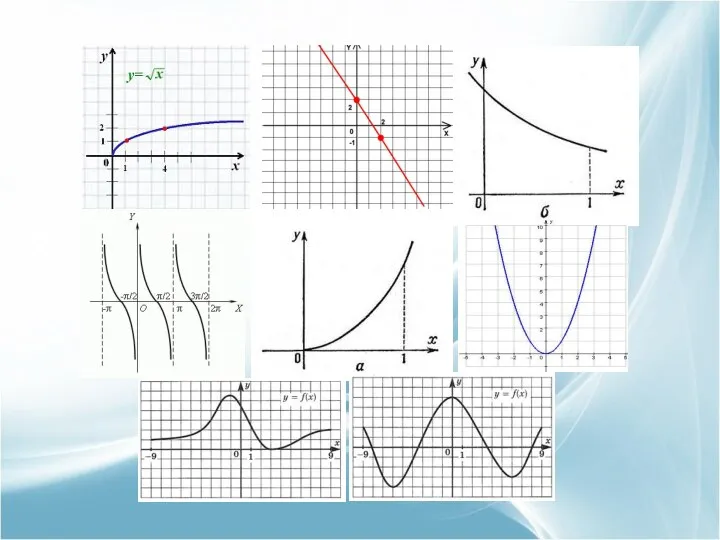
- 6. возрастающая убывающая убывающая убывающая возрастающая возрастающая и убывающая на интервалах возрастающая и убывающая на интервалах возрастающая
- 7. Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не
- 8. Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция в этом интервале монотонно возрастает
- 9. Находим область определения функции f(x). Вычисляем производную f’(x) данной функции. Находим точки, в которых f’(x)=0 или
- 10. Область определения: R. Функция непрерывна. Вычисляем производную : y’=6x²-6x-36. Находим критические точки: y’=0. x²-x-6=0 Д=1-4*(-6)*1=1+24=25 Делим
- 11. Область определения: R. Функция непрерывна. Вычисляем производную : y’=3x²-6x. Находим критические точки: y’=0. x²-2x=0 x(x-2)=0 x1=0
- 12. Точку x=x0 называют точкой минимума функции y=f(x), если у этой точки существует окрестность, для всех точек
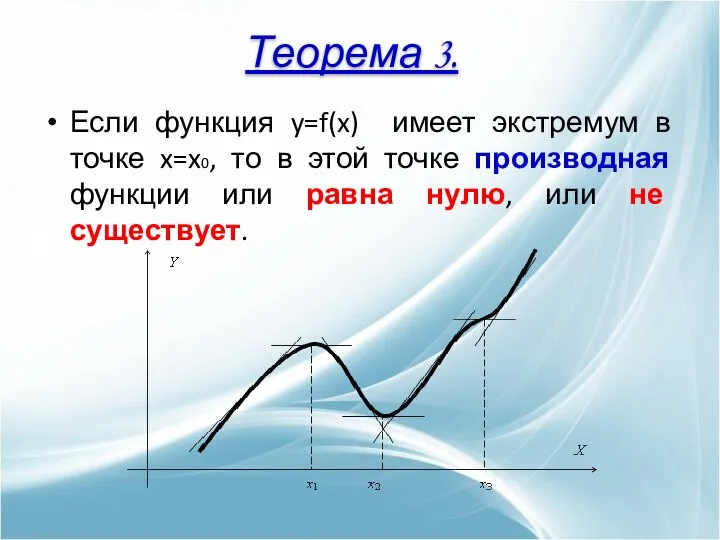
- 13. Если функция y=f(x) имеет экстремум в точке x=x0, то в этой точке производная функции или равна
- 14. Если производная f’(x) при переходе через точку x0 меняет знак, то точка x0 является точкой экстремума
- 15. Область определения: R. Функция непрерывна. Вычисляем производную : y’=-6x²-6x+12. Находим критические точки: y’=0. -x²-x+2=0 Д=1-4*(-1)*2=1+8=9 x1=1;
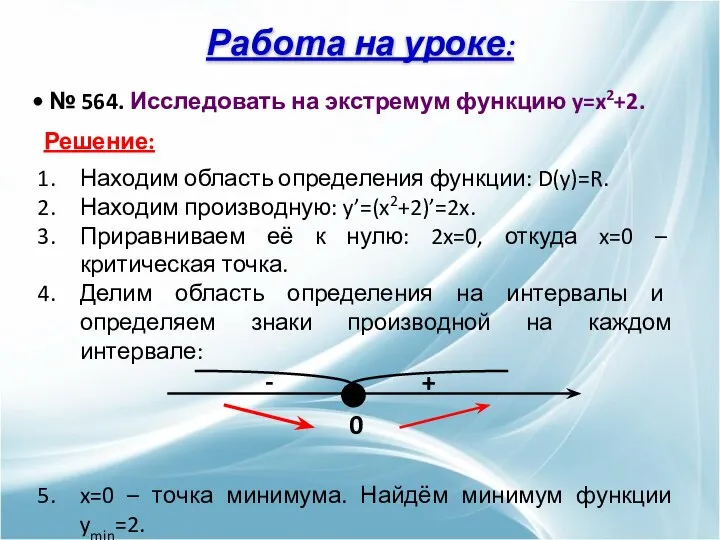
- 16. Работа на уроке: № 564. Исследовать на экстремум функцию y=x2+2. Решение: Находим область определения функции: D(y)=R.
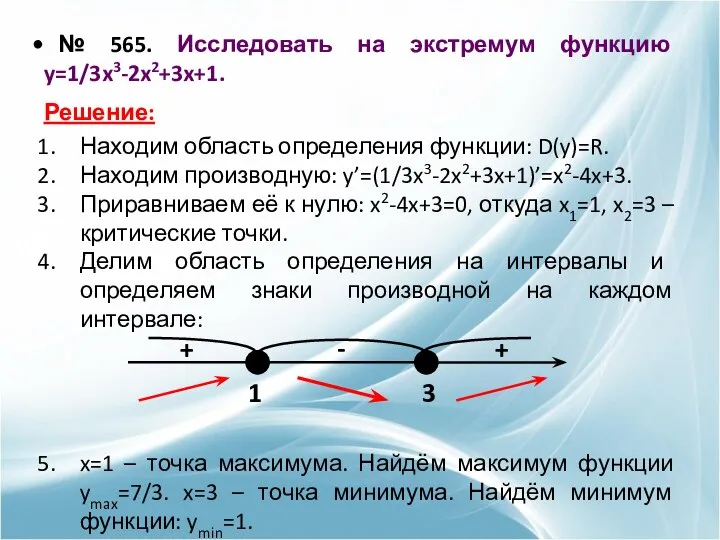
- 17. № 565. Исследовать на экстремум функцию y=1/3x3-2x2+3x+1. Решение: Находим область определения функции: D(y)=R. Находим производную: y’=(1/3x3-2x2+3x+1)’=x2-4x+3.
- 18. № 566. Исследовать на экстремум функцию y=x3+3x2+9x-6. Решение: Находим область определения функции: D(y)=R. Находим производную: y’=(x3+3x2+9x-6)’=3x2+6x+9.
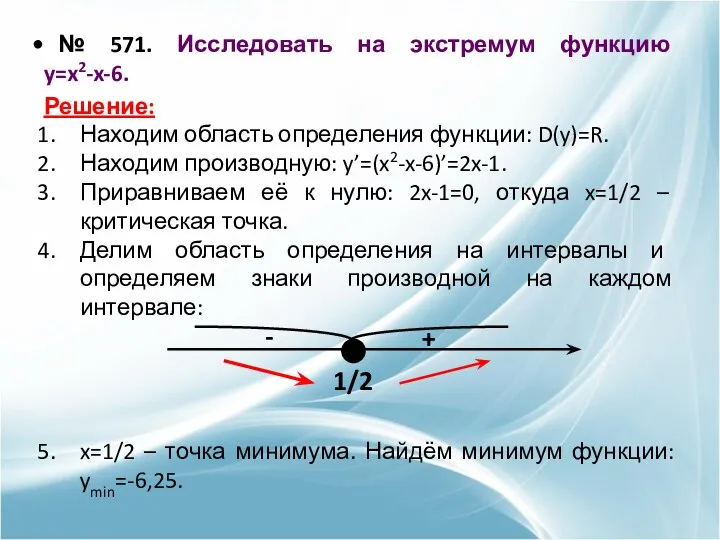
- 19. № 571. Исследовать на экстремум функцию y=x2-x-6. Решение: Находим область определения функции: D(y)=R. Находим производную: y’=(x2-x-6)’=2x-1.
- 21. Скачать презентацию












 Математическая статистика в жизни нашего класса. МАОУ «СОШ №1» с углублённым изучением отдельных предметов им. И. А. Куратова г. Сы
Математическая статистика в жизни нашего класса. МАОУ «СОШ №1» с углублённым изучением отдельных предметов им. И. А. Куратова г. Сы Простейшие показательные уравнения
Простейшие показательные уравнения Линейная алгебра. Определители. (Лекция 2)
Линейная алгебра. Определители. (Лекция 2) Презентация по математике "Числа Бернулли" - скачать
Презентация по математике "Числа Бернулли" - скачать  Комбинаторика. Определение множества
Комбинаторика. Определение множества Обслуговування викликів у СРІ типу M/M/v/L
Обслуговування викликів у СРІ типу M/M/v/L Үш перпендикуляр туралы теорема. Перпендикуляр және көлбеу
Үш перпендикуляр туралы теорема. Перпендикуляр және көлбеу Бинарные отношения и их свойства
Бинарные отношения и их свойства Основы теории нечетких множеств. Логические операции с нечеткими множествами
Основы теории нечетких множеств. Логические операции с нечеткими множествами Викторина «О, счастливчик» (шуточные тесты "математика вокруг нас")
Викторина «О, счастливчик» (шуточные тесты "математика вокруг нас") Третий признак равенства треугольников
Третий признак равенства треугольников Подготовка к сдаче ОГЭ (геометрический блок)
Подготовка к сдаче ОГЭ (геометрический блок) Решение тригонометрических уравнений Работа учителя ГБОУ СОШ №380 Трофименко З. С.
Решение тригонометрических уравнений Работа учителя ГБОУ СОШ №380 Трофименко З. С. Кафедра высшей математики
Кафедра высшей математики Схема независимых испытаний Бернулли
Схема независимых испытаний Бернулли Итоговый урок
Итоговый урок Учет инфляции в финансовых вычислениях
Учет инфляции в финансовых вычислениях Вычисления и преобразования. Значение выражений
Вычисления и преобразования. Значение выражений Презентация по математике "Методы решения тригонометрических уравнений" - скачать
Презентация по математике "Методы решения тригонометрических уравнений" - скачать  Решение тригонометрических и комбинированных уравнений
Решение тригонометрических и комбинированных уравнений Вычисление значений функции по формуле 7 класс
Вычисление значений функции по формуле 7 класс Разложение на множители
Разложение на множители Расстояние от точки до прямой. Перпендикулярные прямые. Урок 94
Расстояние от точки до прямой. Перпендикулярные прямые. Урок 94 Модуль числа
Модуль числа Фракталы. Понятия фрактал и фрактальная геометрия
Фракталы. Понятия фрактал и фрактальная геометрия Мир десятичных дробей
Мир десятичных дробей Прогрессии: арифметическая и геометрическая
Прогрессии: арифметическая и геометрическая Решение тригонометрических уравнений
Решение тригонометрических уравнений