Содержание
- 2. §4 Поверхности второго порядка Поверхности второго порядка описываются уравнениями второго порядка относительно переменных x, y, z.
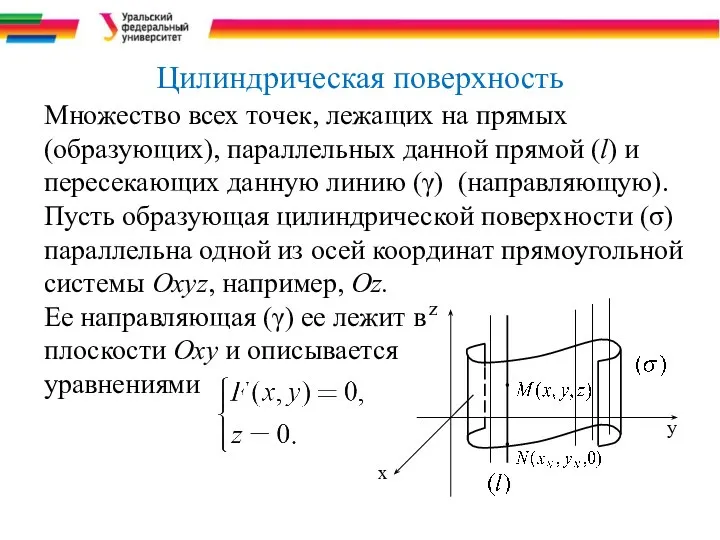
- 3. Цилиндрическая поверхность Множество всех точек, лежащих на прямых (образующих), параллельных данной прямой (l) и пересекающих данную
- 4. Требуется составить уравнение этой цилиндрической поверхности Точка , где (l) – одна из образующих цилиндрической поверхности
- 5. Подставив в равенство (*) вместо хN и yN соответственно х и у, получим равенство F(x,y)=0, которое
- 6. Замечания Уравнение цилиндрической поверхности, подобной рассмотренной, совпадает с уравнением ее направляющей, расположенной в одной из координатных
- 7. Пример. - уравнение цилиндрической поверхности с образующей, параллельной оси Oz (в уравнении отсутствует переменная z), с
- 8. Поверхности второго порядка Общее уравнение поверхности 2-го порядка имеет вид: где .
- 9. Поверхности второго порядка Теорема. Общее уравнение поверхности 2-го порядка с помощью симметрии относительно плоскости, поворота оси
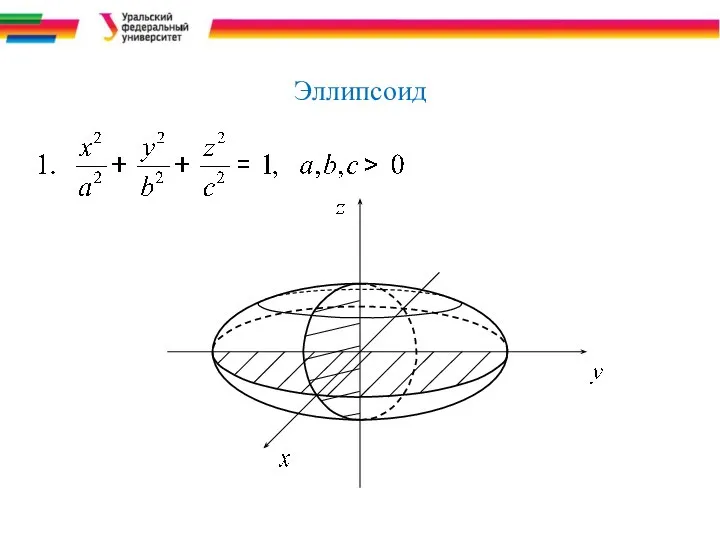
- 10. Эллипсоид
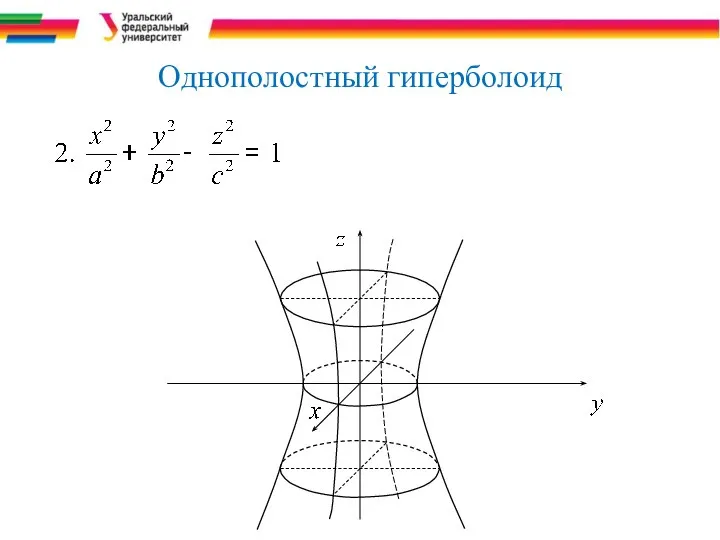
- 11. Однополостный гиперболоид
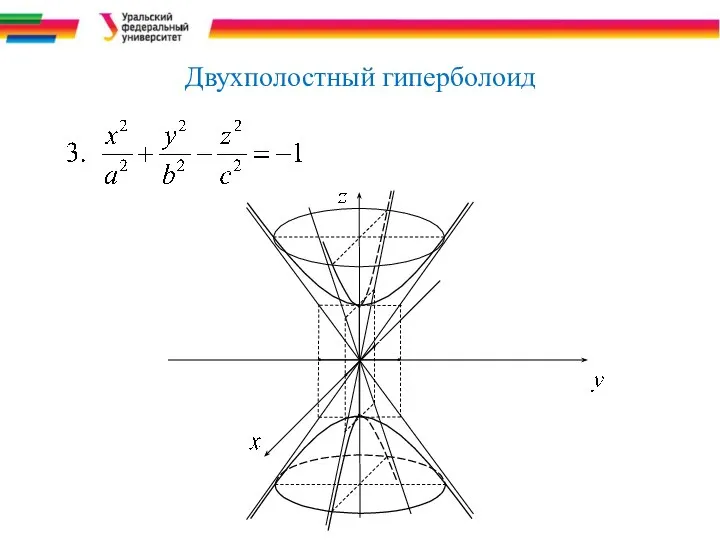
- 12. Двухполостный гиперболоид
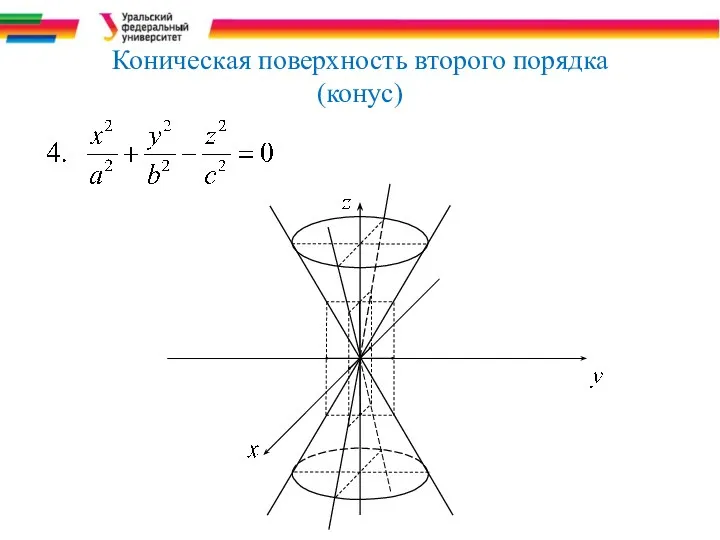
- 13. Коническая поверхность второго порядка (конус)
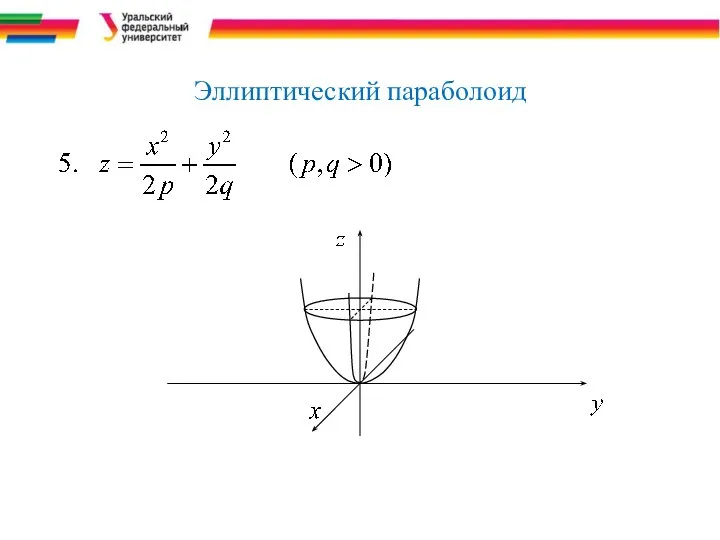
- 14. Эллиптический параболоид
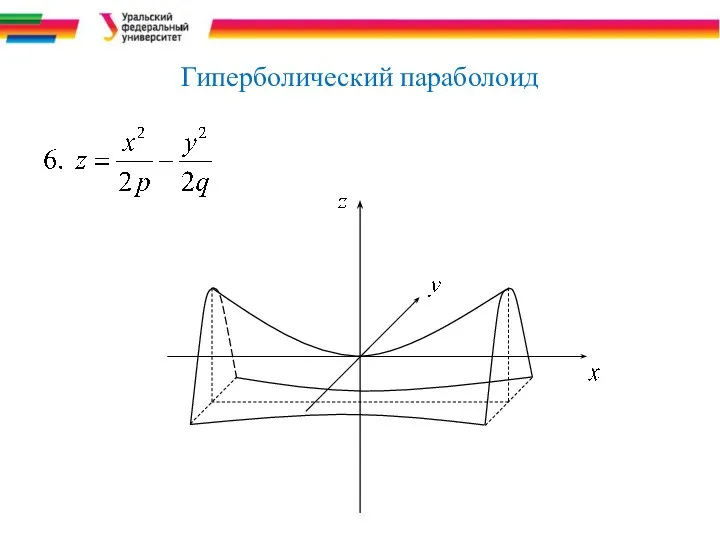
- 15. Гиперболический параболоид
- 16. 7. (a,b>0) – эллиптический цилиндр 8. - гиперболический цилиндр
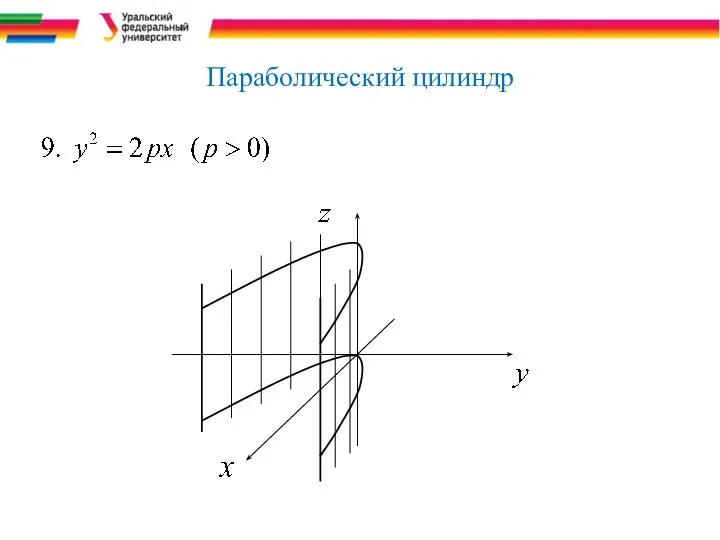
- 17. Параболический цилиндр
- 18. 10. - пара пересекающихся плоскостей, 11. - пара параллельных плоскостей, 12. - пара совпадающих плоскостей, -
- 19. - точка (0, 0, 0) (мнимый конус), - ∅ (мнимый эллипсоид), 16. - ∅ (мнимый эллиптический
- 20. Метод сечений Пересечение исследуемой поверхности с плоскостью дает плоскую кривую. Ряд таких пересечений (называемых сечениями) позволяет
- 21. Метод сечений Из уравнения видно, что эллипсоид представляет собой ограниченную поверхность, заключенную в параллелепипеде Координатные плоскости
- 22. Эллипсоид Дальше исследуем форму эллипсоида по его сечениям плоскостями. Рассмотрим сечение эллипсоида координатной плоскостью Оху. В
- 23. Эллипсоид Аналогично устанавливается сечение данного эллипсоида с плоскостью Oxz - эллипс с полуосями a и с,
- 24. Эллипсоид Рассмотрим теперь сечение эллипсоида с плоскостями , параллельными плоскости Оху. Уравнения линий пересечения будут или
- 25. Эллипсоид Если положить , то уравнения запишутся в виде Отсюда видно, что полуоси и являются действительными
- 26. Эллипсоид При эллипсоид и плоскость пересекаются в одной точке (вырожденный эллипс). Если |h|>c, то эллипсоид и
- 27. Эллипсоид Таким образом, эллипсоид представляет собой ограниченную поверхность, линиями пересечения которой с координатными плоскостями и им
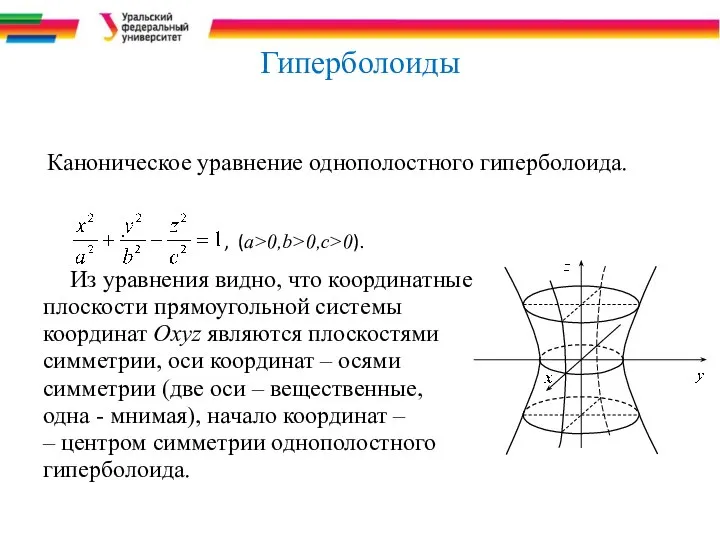
- 28. Гиперболоиды Каноническое уравнение однополостного гиперболоида. , (a>0,b>0,c>0). Из уравнения видно, что координатные плоскости прямоугольной системы координат
- 29. Гиперболоид Исследуем форму этого гиперболоида по его сечениям координатными и параллельными им плоскостями. Линия пересечения гиперболоида
- 30. Гиперболоид Эти уравнения определяют эллипс с полуосями а и b. Линиями пересечения данного гиперболоида с плоскостями
- 31. Гиперболоид Линией пересечения данного гиперболоида с плоскостью Oxz будет гипербола с действительной полуосью Ox и мнимой
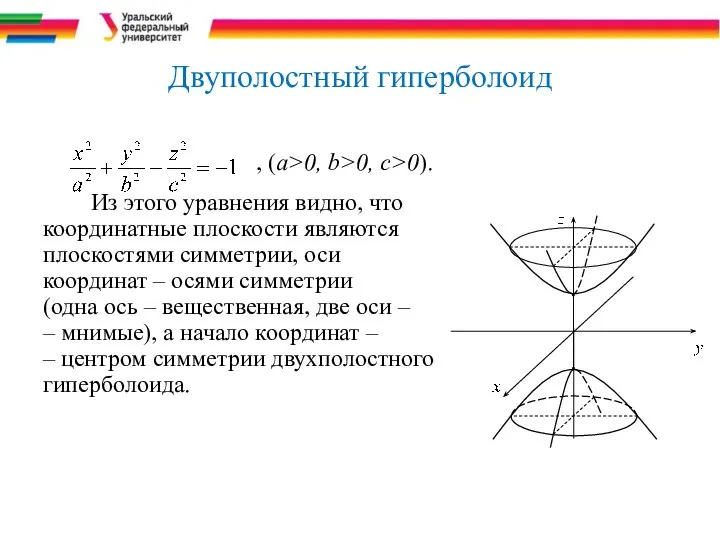
- 32. Двуполостный гиперболоид , (a>0, b>0, c>0). Из этого уравнения видно, что координатные плоскости являются плоскостями симметрии,
- 33. Двуполостный гиперболоид В сечении данного гиперболоида с координатной плоскостью Оху получается мнимый эллипс: Это значит, что
- 34. Двуполостный гиперболоид Линии пересечения данного гиперболоида с плоскостями z=h представляют собой эллипсы, уравнения которых имеют вид:
- 35. Двуполостный гиперболоид Полуоси и являются действительными числами лишь при Это означает, что в пространстве между плоскостями
- 36. Двуполостный гиперболоид Линией пересечения двухполостного гиперболоида с плоскостью Oxz будет гипербола с действительной полуосью с и
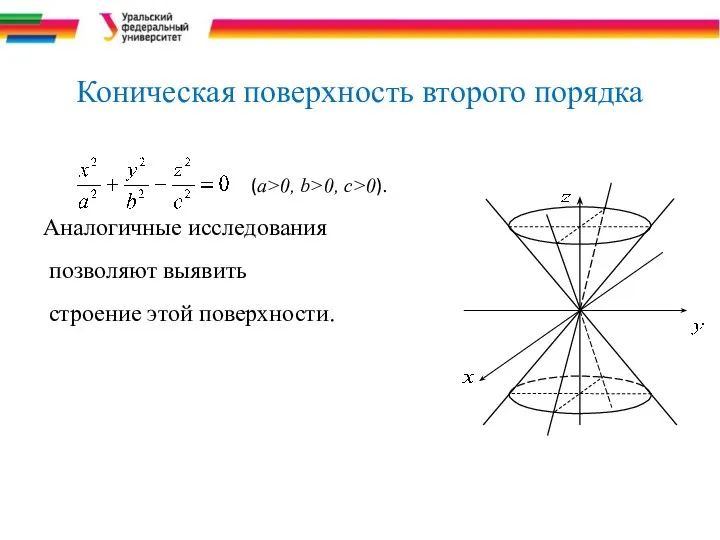
- 37. Коническая поверхность второго порядка (a>0, b>0, c>0). Аналогичные исследования позволяют выявить строение этой поверхности.
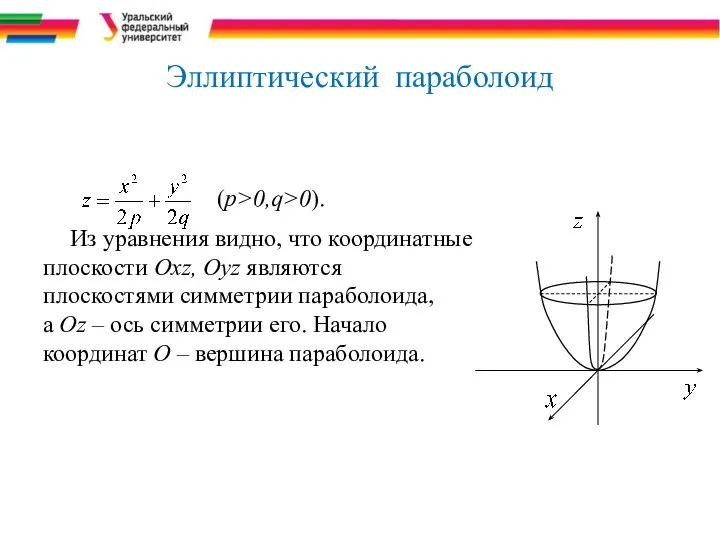
- 38. Эллиптический параболоид (p>0,q>0). Из уравнения видно, что координатные плоскости Охz, Оуz являются плоскостями симметрии параболоида, а
- 40. Скачать презентацию

























 Уравнения прямой и окружности
Уравнения прямой и окружности Построение сечений тетраэдра. (10 класс)
Построение сечений тетраэдра. (10 класс) Арифметический квадратный корень
Арифметический квадратный корень Алгоритм письменного умножения многозначного числа на двузначное
Алгоритм письменного умножения многозначного числа на двузначное Тригонометрия. Формулы приведения
Тригонометрия. Формулы приведения Переключательные схемы
Переключательные схемы Умозаключения
Умозаключения Построение графиков. Общая схема построения
Построение графиков. Общая схема построения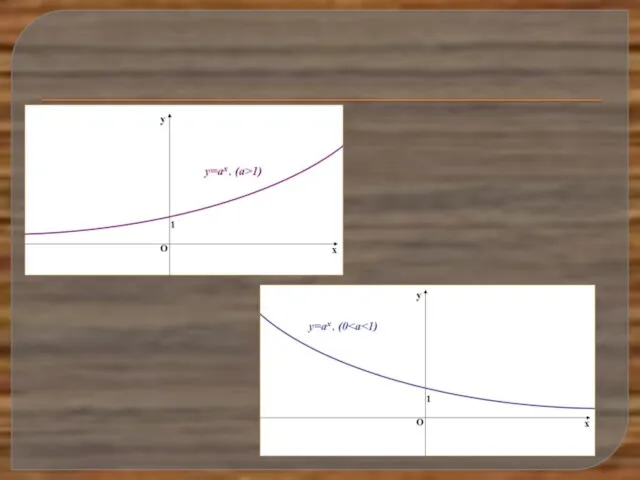 Понятие логарифма
Понятие логарифма Статистика – дизайн информации
Статистика – дизайн информации Величины и их измерение
Величины и их измерение Какие числа не употребляются в математике?
Какие числа не употребляются в математике? Задачи на увеличение (уменьшение) числа на несколько единиц
Задачи на увеличение (уменьшение) числа на несколько единиц Элементы стереометрии
Элементы стереометрии 5 КЛАСС ОБОБЩАЮЩИЙ УРОК ПО ТЕМЕ «НАТУРАЛЬНЫЕ ЧИСЛА»
5 КЛАСС ОБОБЩАЮЩИЙ УРОК ПО ТЕМЕ «НАТУРАЛЬНЫЕ ЧИСЛА»  Случайные события и вероятность
Случайные события и вероятность Геометрические фигуры нашего города
Геометрические фигуры нашего города Способы проверки правильности результатов вычислений
Способы проверки правильности результатов вычислений Золотое сечение и числа Фибоначчи
Золотое сечение и числа Фибоначчи Сложная функция
Сложная функция Описанная окружность
Описанная окружность Преобразование сумм тригонометрических функций в произведение
Преобразование сумм тригонометрических функций в произведение Математические термины
Математические термины Презентация по математике "ЕДИНИЦА ВРЕМЕНИ - СЕКУНДА (4 КЛАСС)" - скачать бесплатно
Презентация по математике "ЕДИНИЦА ВРЕМЕНИ - СЕКУНДА (4 КЛАСС)" - скачать бесплатно Натуральные числа. Обобщение и систематизация знаний
Натуральные числа. Обобщение и систематизация знаний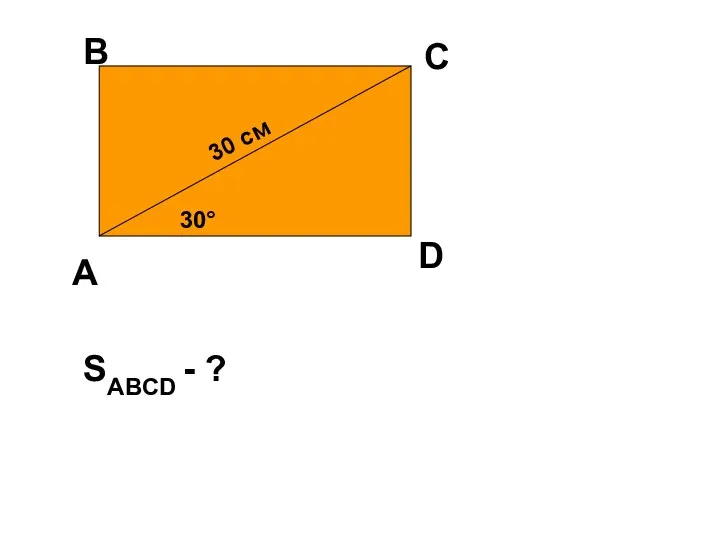 Параметры четырехугольника
Параметры четырехугольника Методы выбора и принятия решений
Методы выбора и принятия решений Понятие формы. Многообразие форм окружающего мира. 6 класс
Понятие формы. Многообразие форм окружающего мира. 6 класс