Содержание
- 2. Векторы на плоскости Понятие вектора. Равенство векторов Векторные величины в отличие от скалярных имеют не только
- 3. Векторы называют равными, если они сонаправленны и их модули равны. А В C D AB =
- 4. Сложение и вычитание векторов 1) Сложение векторов по правилу треугольника. Пусть даны векторы а и b
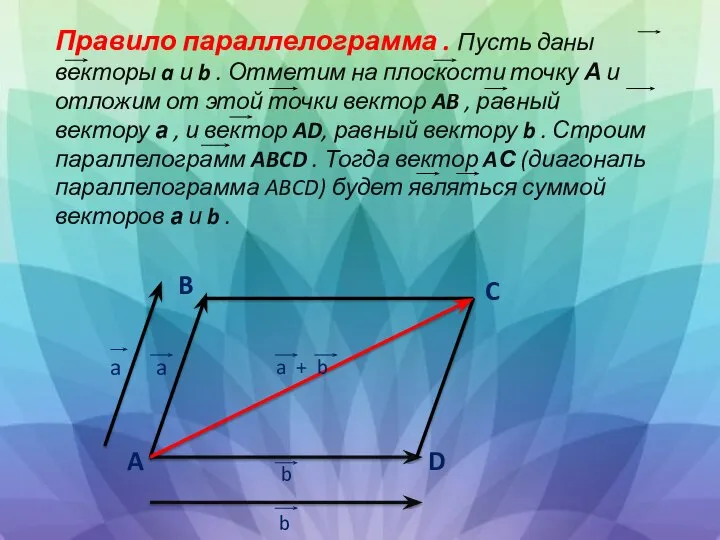
- 5. Правило параллелограмма . Пусть даны векторы a и b . Отметим на плоскости точку А и
- 6. 2) Свойства сложения векторов: 1. Для любых двух векторов а и b верно равенство : a
- 7. 5) Пусть прямые a и b пересекаются в точке О. отложим данный вектор с от точки
- 8. Умножение вектора на число 1) Произведением вектора а ≠ 0 на число R называется вектор ,
- 9. 3) Свойства умножения числа на вектор: Для любых чисел α и β и любых векторов a
- 10. Угол между векторами. Скалярное произведение векторов Углом между векторами AB и АС называется угол BAC .
- 11. 2) Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между
- 12. Координаты вектора 1) Теорема о разложении вектора по двум неколлинеарным векторам: Если ненулевые векторы а и
- 13. 2) Базисные векторы - выбранные на плоскости два неколлинеарных вектора, по которым производится разложение заданного вектора.
- 14. Различные способы задания прямой в прямоугольной системе координат 1) Направляющий вектор прямой - это любой ненулевой
- 16. Скачать презентацию












 Методы интегрирования
Методы интегрирования Решение задач по теме «Параллелограмм»
Решение задач по теме «Параллелограмм» Многогранники. Гимнастика ума
Многогранники. Гимнастика ума Табличное сложение и вычитание
Табличное сложение и вычитание Решение задач Выполнила Хижняк Светлана Анатольевна Учитель МБОУ СОШ №9, город Златоуст, Челябинская область. 2010 год
Решение задач Выполнила Хижняк Светлана Анатольевна Учитель МБОУ СОШ №9, город Златоуст, Челябинская область. 2010 год  Геометрическая прогрессия
Геометрическая прогрессия Алгоритм нахождения наименьшего и наибольшего значений показательной функции
Алгоритм нахождения наименьшего и наибольшего значений показательной функции Циклический алгоритм на QBASIC. Вложенные циклы
Циклический алгоритм на QBASIC. Вложенные циклы Вычитание смешанных дробей
Вычитание смешанных дробей Производная функции
Производная функции Теорема Пифагора. Задачи
Теорема Пифагора. Задачи Элективный курс «Алгебра модуля»
Элективный курс «Алгебра модуля» Наибольший общий делитель. 5 класс
Наибольший общий делитель. 5 класс Сложение и вычитание дробей с разными знаменателями. 6 класс
Сложение и вычитание дробей с разными знаменателями. 6 класс Математичні софізми
Математичні софізми Представьте числа в виде суммы разрядных слагаемых
Представьте числа в виде суммы разрядных слагаемых Использование триангуляции при моделировании сложных объектов
Использование триангуляции при моделировании сложных объектов Интегральные исчисления
Интегральные исчисления Загадочный мир фракталов
Загадочный мир фракталов Функции нескольких переменных
Функции нескольких переменных Математики и математика в годы Великой Отечественной войны
Математики и математика в годы Великой Отечественной войны Алгебра логики
Алгебра логики Параллелограмм
Параллелограмм Сфера. Сфеерическая геометрия
Сфера. Сфеерическая геометрия Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Коэффициенты линейной функции
Коэффициенты линейной функции Відомі математики
Відомі математики Параллельные прямые
Параллельные прямые