Вычисление площадей плоских фигур. Вычисление объема тела вращения. Несобственный интеграл. Лекция 13
Содержание
- 2. Вычисление площадей плоских фигур По геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, расположенной выше оси ОХ
- 3. Площадь фигуры, ограниченной кривыми y = f1(x) и y = f2(x), прямыми x = a, x
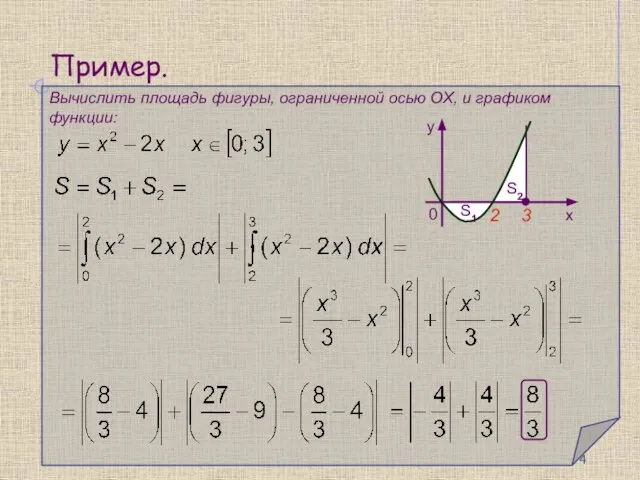
- 4. Пример. Вычислить площадь фигуры, ограниченной осью OX, и графиком функции: 2 3 S1 S2
- 5. Вычисление длины дуги плоской кривой Если уравнение кривой AB задано в параметрической форме: то длина дуги
- 6. Пример. Вычислить длину дуги окружности, заданной уравнением: от точки А(2; 0) до точки 2 А В
- 7. Вычисление объема тела вращения Пусть вокруг оси OX вращается криволинейная трапеция, ограниченная непрерывной линией y =
- 8. Пример. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями: 4 вокруг оси OY.
- 10. Несобственный интеграл Определенный интеграл Так называемые несобственные интегралы бывают двух видов: Определенный интеграл от непрерывной функции,
- 11. Несобственный интеграл 1 рода Пусть функция f(x) непрерывна на промежутке то его называют несобственным интегралом первого
- 12. Несобственный интеграл с двумя бесконечными пределами определяется формулой: В этом случае интеграл слева сходится лишь тогда,
- 13. Примеры. Вычислить несобственные интегралы или установить их расходимость. Интеграл расходится Интеграл расходится, так как такой предел
- 15. Признак сравнения
- 16. Несобственный интеграл 2 рода Пусть функция f(x) непрерывна на промежутке то его называют несобственным интегралом второго
- 17. Если функция f(x) терпит разрыв во внутренней точке c отрезка [a; b] , то несобственный интеграл
- 18. Вычислить несобственный интеграл или установить его расходимость. Интеграл расходится Пример.
- 19. Несобственные интегралы от неограниченных функций. Примеры Признак сравнения для таких интегралов
- 20. Несобственные интегралы от неограниченных функций. Признак сравнения
- 22. Скачать презентацию


















 Параллельное проектирование
Параллельное проектирование Основы теории относительности
Основы теории относительности Единицы массы. Грамм
Единицы массы. Грамм Прямоугольный параллелепипед
Прямоугольный параллелепипед Екіфакторлы дисперсиялық талдау
Екіфакторлы дисперсиялық талдау Процедуры и функции работы со строками
Процедуры и функции работы со строками Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел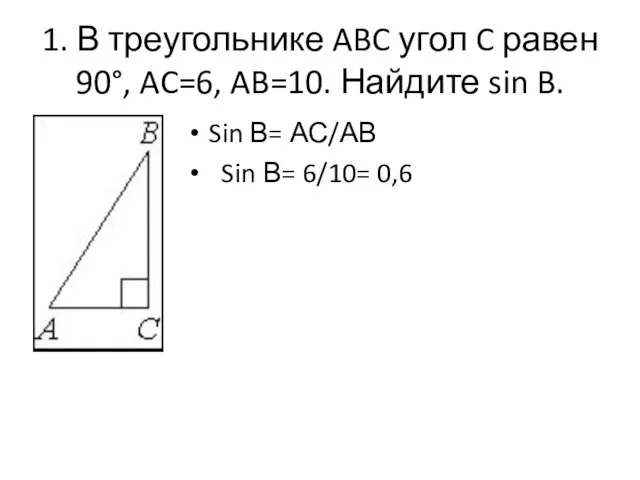 Треугольник. Углы
Треугольник. Углы Автор презентации Учитель МОУ СОШ №11 Юдина О.А.
Автор презентации Учитель МОУ СОШ №11 Юдина О.А.  Статистика населения
Статистика населения Средние величины и показатели вариации
Средние величины и показатели вариации Аттестационная работа. Путешествие с математикой по родному городу
Аттестационная работа. Путешествие с математикой по родному городу Преобразование графиков элементарных функций
Преобразование графиков элементарных функций Конформные отображения
Конформные отображения Десятичные дроби и действия над ними
Десятичные дроби и действия над ними  Обзор численных методов
Обзор численных методов Предельные теоремы теории вероятностей и закон больших чисел
Предельные теоремы теории вероятностей и закон больших чисел Надежность производственных и технологических систем. Математические модели в теории надежности
Надежность производственных и технологических систем. Математические модели в теории надежности Счет в пределах 20. Подготовка к введению задач в два действия
Счет в пределах 20. Подготовка к введению задач в два действия Статическая устойчивость
Статическая устойчивость Тема урока: Чертеж болтового соединения Цель урока: мы должны выяснить порядок построения чертежа болтового соединения и вы
Тема урока: Чертеж болтового соединения Цель урока: мы должны выяснить порядок построения чертежа болтового соединения и вы Высказывание. Операции над высказываниями
Высказывание. Операции над высказываниями Гарфилд изучает дроби
Гарфилд изучает дроби В поисках клада! Интерактивное занятие по математике в средней группе
В поисках клада! Интерактивное занятие по математике в средней группе Занимательные задачи. Тест по математике 1 класс
Занимательные задачи. Тест по математике 1 класс Геометрическая прогрессия
Геометрическая прогрессия График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Общие вопросы изучения нумерации
Общие вопросы изучения нумерации