- Главная
- Математика
- Вычислительная механика. Аппроксимация дифференциальных операторов

Содержание
- 2. Обыкновенные дифференциальные уравнения Дифференциальные уравнения в частных производных - задачи химической кинетики, - электрических цепей, движение
- 3. Суть метода сеток заключается в покрытии расчетной области (x,t) сеткой из I×N точек (см. рис), что
- 4. Построение разностной схемы конечно-разностная схема Конечно-разностная схема называется устойчивой, если малым изменениям входных данных соответствует малое
- 5. Явная разностная схема
- 6. Неявная разностная схема
- 7. МКР для многомерных задач Вводим сетку + граничные и начальные условия Условие устойчивости Сходимость иначе
- 9. Скачать презентацию
Обыкновенные дифференциальные уравнения
Дифференциальные уравнения в частных производных
- задачи химической кинетики,
-
Обыкновенные дифференциальные уравнения
Дифференциальные уравнения в частных производных
- задачи химической кинетики,
-
движение систем взаимодействующих
материальных точек
- и другие задачи физики, химии, техники
задачи математической физики,
гидродинамики,
акустики
и других областей знаний.
Решение дифференциальных уравнений
аналитические
численные
- точные – методы позволяют выразить решение дифференциальных уравнений через элементарные функции (в аналитическом виде);
- приближенные – методы, в которых решение получается как предел некоторой последовательности, члены которой выражаются через элементарные функции.
-численные методы не позволяют найти точное решение дифференциальных уравнений в аналитической форме. С их помощью получается таблица приближенных (иногда точных) значений искомого решения в некоторых точках рассматриваемой области решения, именуемых сеткой. В силу этого численные методы называют иначе разностными методами или методами сеток.
Суть метода сеток заключается в покрытии расчетной области (x,t) сеткой из
Суть метода сеток заключается в покрытии расчетной области (x,t) сеткой из
Сеткой определяются узлы, в которых будет осуществляться поиск решения.
Далее необходимо заменить дифференциальные уравнения в частных производных (уравнение диффузии, уравнение теплопроводности и др.) аппроксимирующими их уравнениями в конечных разностях, выписав соответствующие разностные уравнения для каждого (i,n)-гo узла сетки.
Понятие разностной схемы
Совокупность разностных уравнений, построенных на сетке и аппроксимирующих основное дифференциальное уравнение на V и краевые условия на Г, называется разностной схемой.
Таким образом, вместо поиска непрерывных зависимостей u(x) реализация разностной схемы позволяет отыскать значения функции в узлах сетки. Ее поведение в промежутках между узлами может быть получено при помощи построения какой-либо интерполяции.
конечные разности на сетке
Построение разностной схемы
конечно-разностная схема
Конечно-разностная схема называется устойчивой, если малым изменениям входных
Построение разностной схемы
конечно-разностная схема
Конечно-разностная схема называется устойчивой, если малым изменениям входных
Если р.с. устойчива и аппроксимирует исходную краевую задачу с порядком n, то она сходиться, причем скорость сходимости равна порядку аппроксимации.
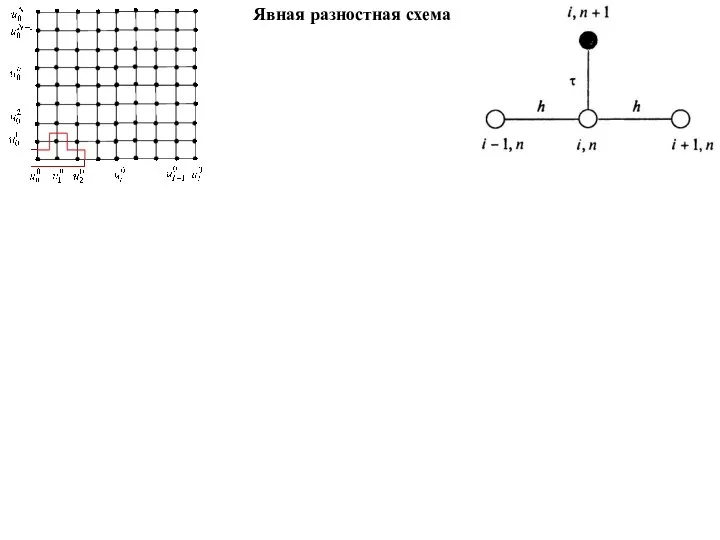
Явная разностная схема
Явная разностная схема
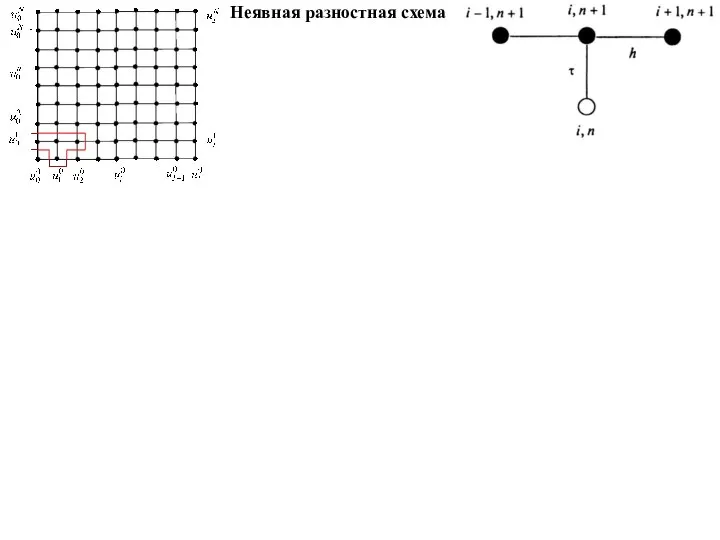
Неявная разностная схема
Неявная разностная схема
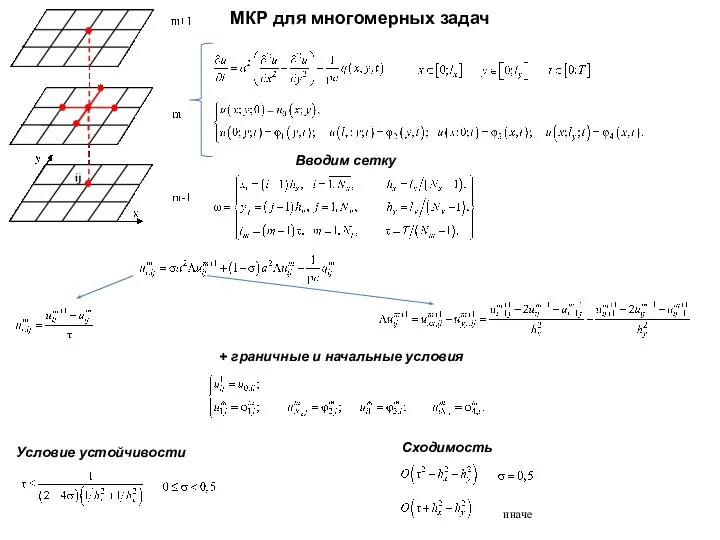
МКР для многомерных задач
Вводим сетку
+ граничные и начальные условия
Условие устойчивости
Сходимость
иначе
МКР для многомерных задач
Вводим сетку
+ граничные и начальные условия
Условие устойчивости
Сходимость
иначе



 Как часто в жизни используются дроби?
Как часто в жизни используются дроби? Слабое звено
Слабое звено Чтение свойств производной функции по графику этой функции
Чтение свойств производной функции по графику этой функции Презентация по математике "Программно-аппаратный комплекс" - скачать бесплатно
Презентация по математике "Программно-аппаратный комплекс" - скачать бесплатно Метод Математической Индукции
Метод Математической Индукции Десятичные и натуральные логарифмы. Формула перехода к другому основанию. (10 класс)
Десятичные и натуральные логарифмы. Формула перехода к другому основанию. (10 класс) Приближённые вычисления с десятичными дробями
Приближённые вычисления с десятичными дробями Презентация по математике "Решение задач с помощью уравнений (5 класс)" - скачать
Презентация по математике "Решение задач с помощью уравнений (5 класс)" - скачать  Умножение на 2
Умножение на 2 Задание 1 с пометками
Задание 1 с пометками Иррациональные уравнения
Иррациональные уравнения Волшебная страна - Геометрия. Старинная мера длины
Волшебная страна - Геометрия. Старинная мера длины Золотое сечение в искусстве Выполнен учащейся 4 класса МОУ ДОД «Котовская детская школа искусств» Тамбовской области Поповой
Золотое сечение в искусстве Выполнен учащейся 4 класса МОУ ДОД «Котовская детская школа искусств» Тамбовской области Поповой 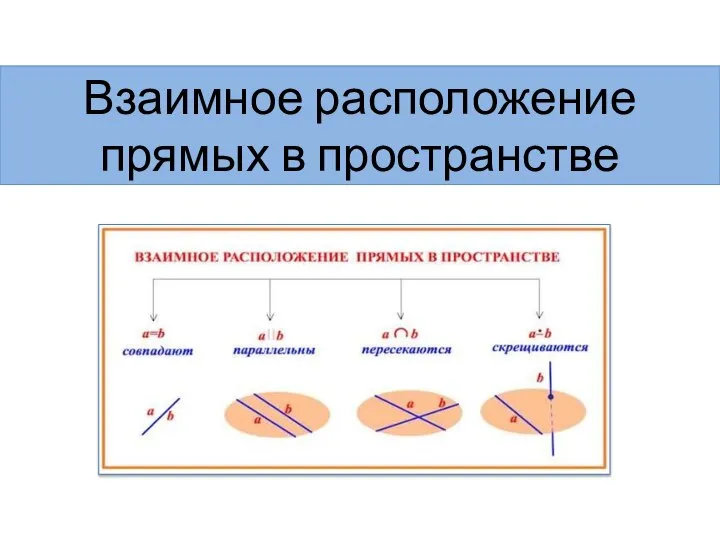 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Системы линейных уравнений
Системы линейных уравнений Презентация по математике "Вычисления с многозначными числами" - скачать
Презентация по математике "Вычисления с многозначными числами" - скачать  Прямая пропорциональность (7 класс)
Прямая пропорциональность (7 класс) Деление положительных десятичных дробей. Презентация Кружилиной Арины, ученицы 6 «Б» класса_
Деление положительных десятичных дробей. Презентация Кружилиной Арины, ученицы 6 «Б» класса_ Сказка о стране чисел Автор: Борисенко Максим Романович Руководитель: Суслакова Вера Алексеевна
Сказка о стране чисел Автор: Борисенко Максим Романович Руководитель: Суслакова Вера Алексеевна Статистика. Необходимость возникновения статистики-науки
Статистика. Необходимость возникновения статистики-науки Автоматическое планирование траектории. Программа для оптимального поиска пути от одной точки до другой в двумерном пространстве
Автоматическое планирование траектории. Программа для оптимального поиска пути от одной точки до другой в двумерном пространстве Основные тригонометрические формулы
Основные тригонометрические формулы Cложение и вычитание чисел с разными знаками
Cложение и вычитание чисел с разными знаками Решение задач на совместную работу при подготовке учащихся 9-х классов к ГИА
Решение задач на совместную работу при подготовке учащихся 9-х классов к ГИА Функции одного переменного
Функции одного переменного Құрама кері есептер
Құрама кері есептер Тренажёр Помоги Снеговику. Математика 1 класс
Тренажёр Помоги Снеговику. Математика 1 класс Аттестационная работа. Образовательная программа элективного курса. За страницами учебника алгебры
Аттестационная работа. Образовательная программа элективного курса. За страницами учебника алгебры