Содержание
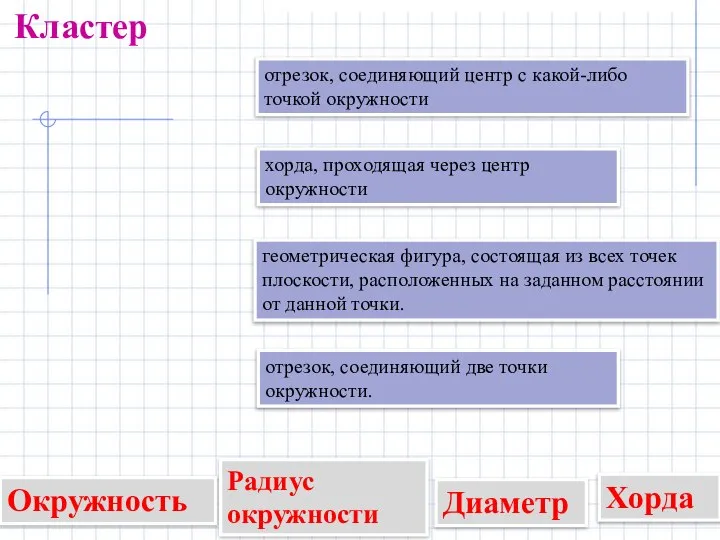
- 2. Окружность геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Радиус
- 3. Геометрия - 7 Задачи на построение Учебник "Геометрия 7-9" Автор Л.С. Атанасян
- 4. В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и
- 5. Анализ. Предположить, что задача решена, сделать примерный чертеж искомой фигуры, отметить те отрезки и углы, которые
- 6. Построение с помощью циркуля и линейки Решение простейших задач на построение циркулем и линейкой. 1. На
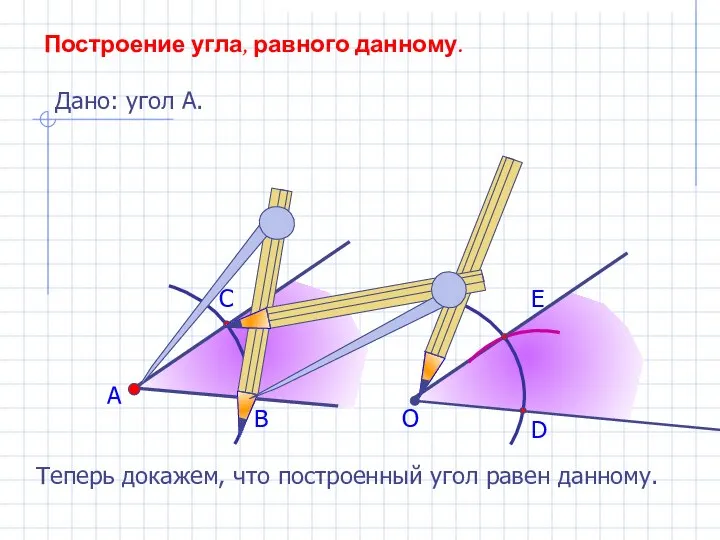
- 7. А В С Построение угла, равного данному. Дано: угол А. О D E Теперь докажем, что
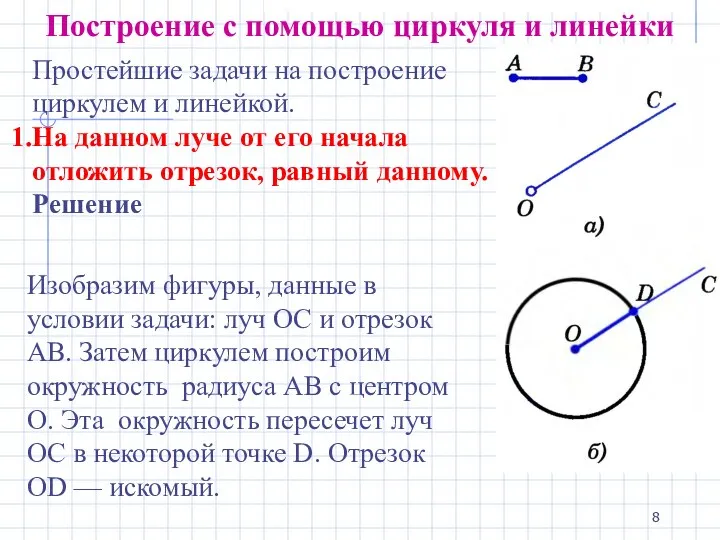
- 8. Построение с помощью циркуля и линейки Простейшие задачи на построение циркулем и линейкой. На данном луче
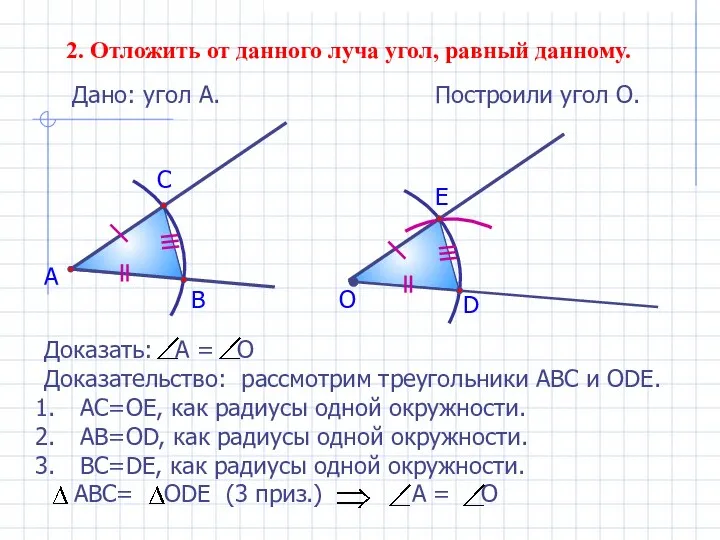
- 9. 2. Отложить от данного луча угол, равный данному. Дано: угол А. А Построили угол О. В
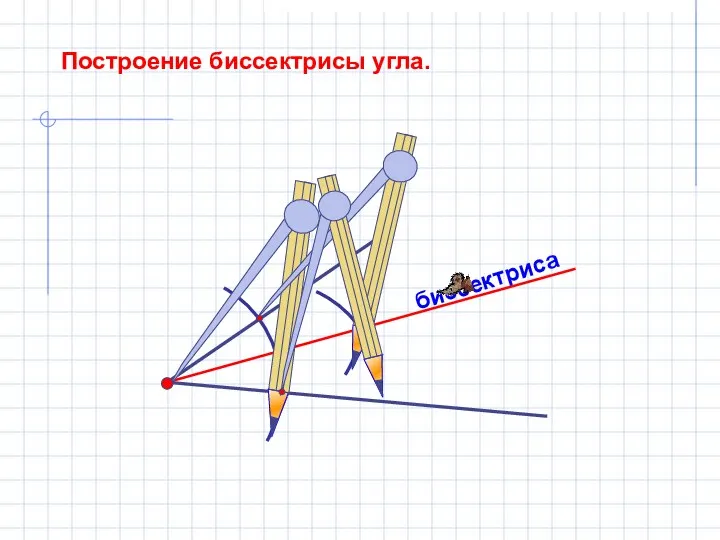
- 10. биссектриса Построение биссектрисы угла.
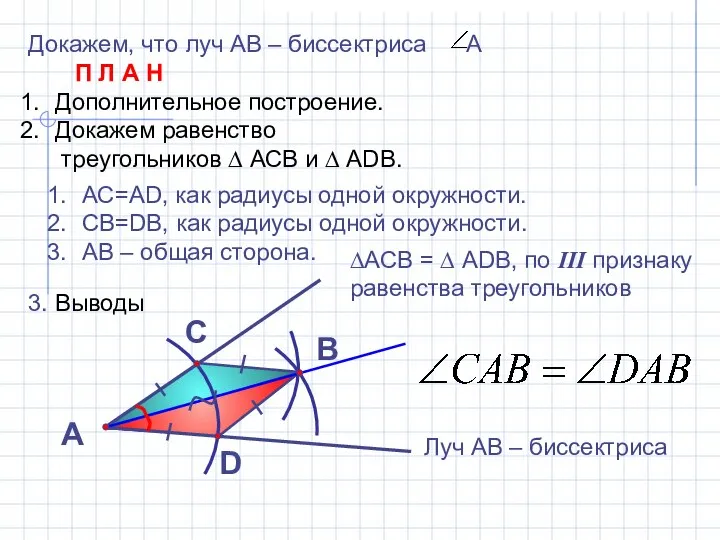
- 11. Докажем, что луч АВ – биссектриса А П Л А Н Дополнительное построение. Докажем равенство треугольников
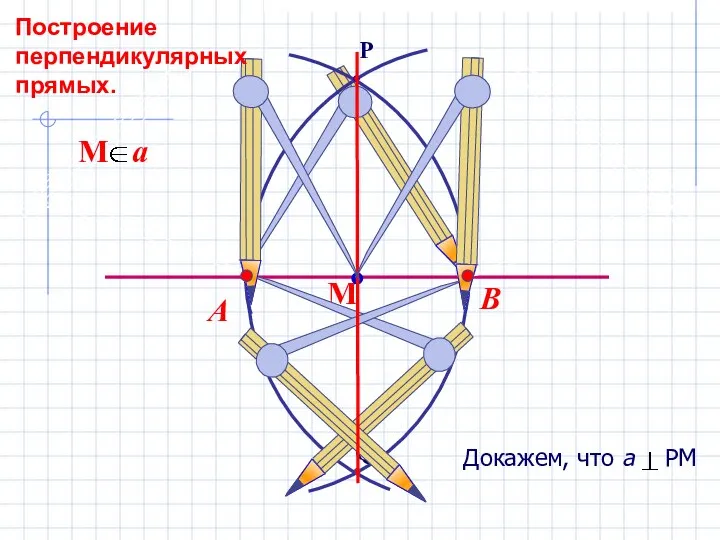
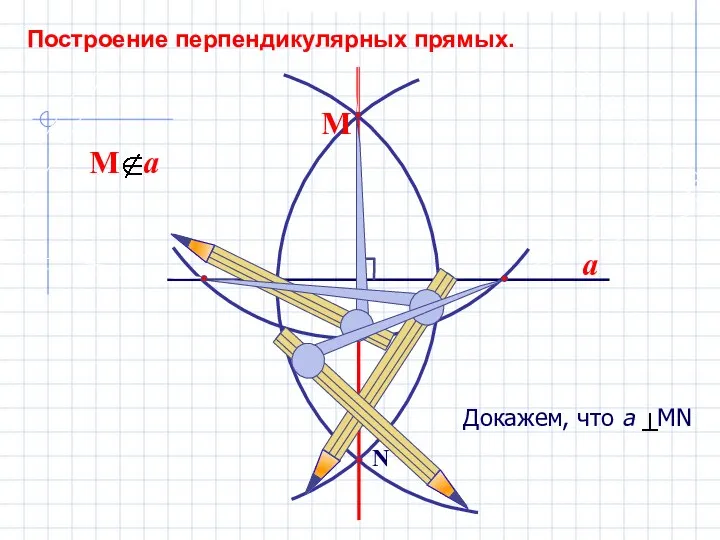
- 12. В А Построение перпендикулярных прямых.
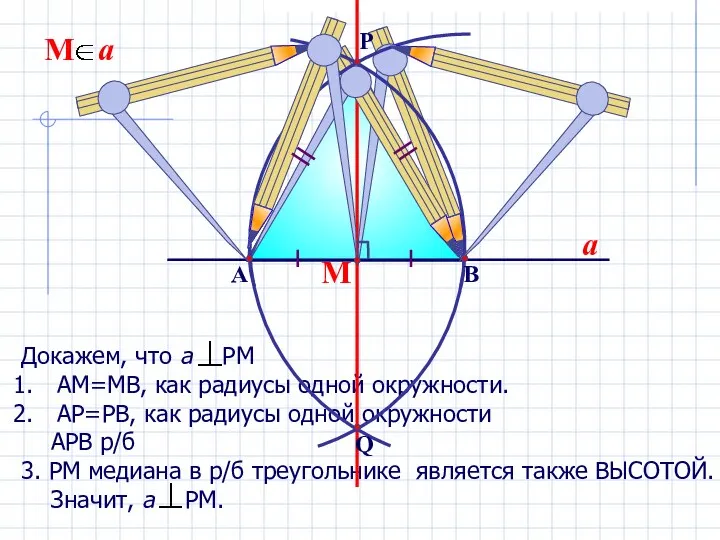
- 13. Докажем, что а РМ АМ=МВ, как радиусы одной окружности. АР=РВ, как радиусы одной окружности АРВ р/б
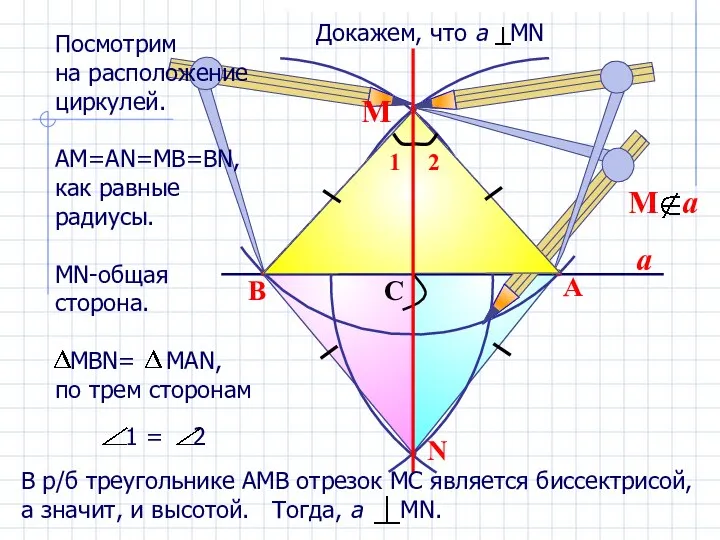
- 14. a N М Построение перпендикулярных прямых.
- 15. a N B A C М Посмотрим на расположение циркулей. АМ=АN=MB=BN, как равные радиусы. МN-общая сторона.
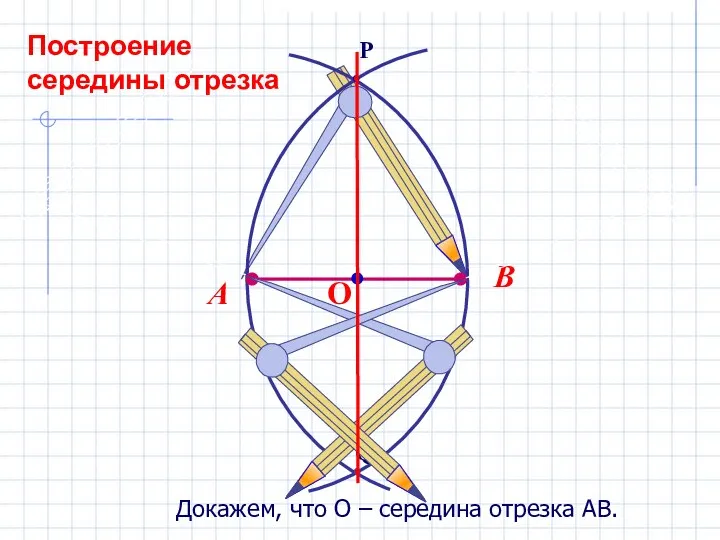
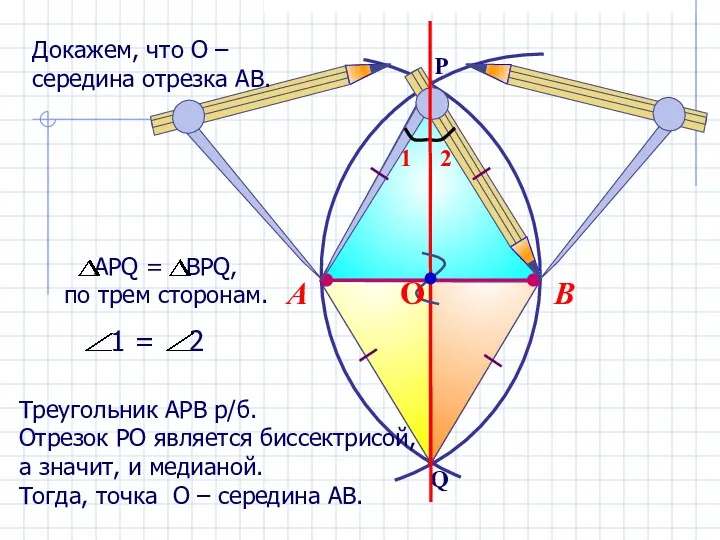
- 16. Докажем, что О – середина отрезка АВ. Построение середины отрезка
- 17. В А Треугольник АРВ р/б. Отрезок РО является биссектрисой, а значит, и медианой. Тогда, точка О
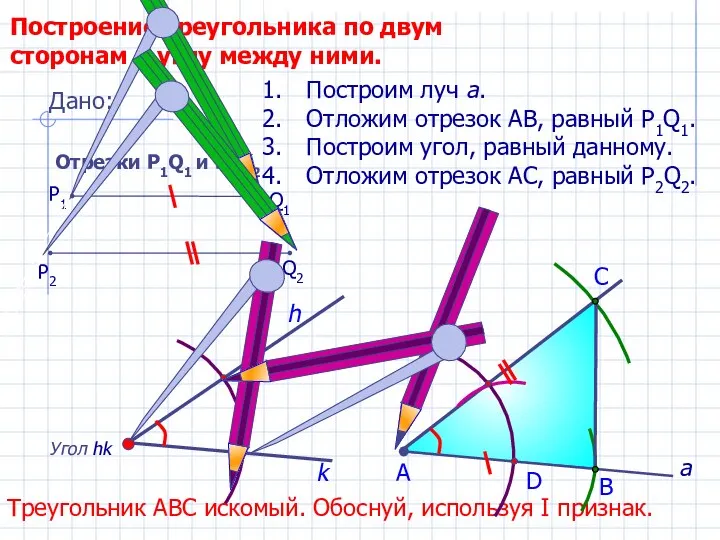
- 18. D С Построение треугольника по двум сторонам и углу между ними. Угол hk h Построим луч
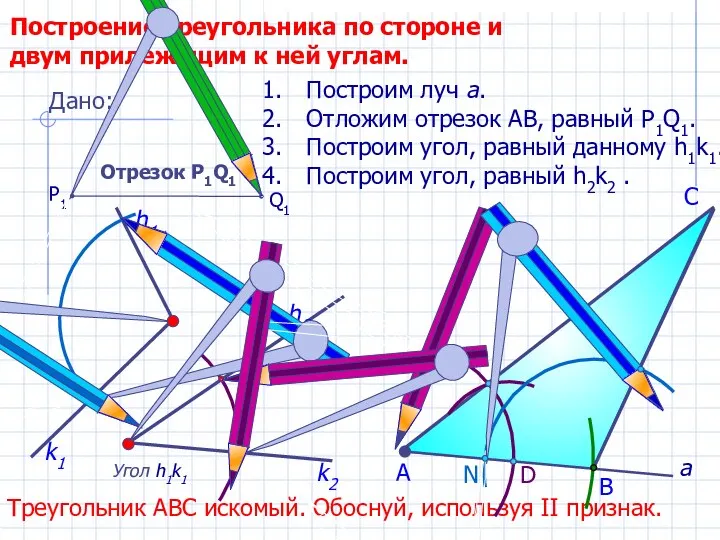
- 19. D С Построение треугольника по стороне и двум прилежащим к ней углам. Угол h1k1 h2 Построим
- 21. Скачать презентацию




 Презентация по математике "«Сложение и вычитание 5 ». Закрепление" - скачать
Презентация по математике "«Сложение и вычитание 5 ». Закрепление" - скачать  Прямоугольные треугольники. Свойства прямоугольных треугольников
Прямоугольные треугольники. Свойства прямоугольных треугольников Повышение уровня самоподготовки к ОГЭ по математике. Функции и графики
Повышение уровня самоподготовки к ОГЭ по математике. Функции и графики Презентация по математике "Умножение с 0 и 1" - скачать
Презентация по математике "Умножение с 0 и 1" - скачать  Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле
Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле Вводное повторение.Геометрия 8 класс
Вводное повторение.Геометрия 8 класс Основные свойства простейших геометрических фигур. Геометрические фигуры: точка, прямая, отрезок
Основные свойства простейших геометрических фигур. Геометрические фигуры: точка, прямая, отрезок Четырехугольники. Обобщающий урок геометрии 8 класс
Четырехугольники. Обобщающий урок геометрии 8 класс Презентация Тектология А.А.Богданова при формировании гуманитарных подходов корпоративной социальной ответственности Курчина М
Презентация Тектология А.А.Богданова при формировании гуманитарных подходов корпоративной социальной ответственности Курчина М Використання програмних засобів для розв’язування системи лінійних рівнянь
Використання програмних засобів для розв’язування системи лінійних рівнянь Игра-викторина на звание лучшего математика класса
Игра-викторина на звание лучшего математика класса Конус
Конус Второй признак равенства треугольников
Второй признак равенства треугольников Размещения и сочетания множеств
Размещения и сочетания множеств Методы исследования математических моделей
Методы исследования математических моделей Екіфакторлы дисперсиялық талдау
Екіфакторлы дисперсиялық талдау Практический расчёт, оценка и прикидка. Подготовка к ЕГЭ (1)
Практический расчёт, оценка и прикидка. Подготовка к ЕГЭ (1) Презентация к уроку математики по теме: применение формул сокращенного умножения к преобразованию алгебраических выражений. 7 кла
Презентация к уроку математики по теме: применение формул сокращенного умножения к преобразованию алгебраических выражений. 7 кла Подготовка к ЕГЭ по математике. Решение задач В11
Подготовка к ЕГЭ по математике. Решение задач В11 Презентация по математике "Отрезок. Прямая. Луч." - скачать
Презентация по математике "Отрезок. Прямая. Луч." - скачать  Задачи на совместное выполнение работы
Задачи на совместное выполнение работы Функция. Классификация функций. Основные свойства функций. Понятие функции. (Семинар 3)
Функция. Классификация функций. Основные свойства функций. Понятие функции. (Семинар 3) Решение задач
Решение задач Логарифмические спирали
Логарифмические спирали Способы решений уравнений и неравенств с параметром
Способы решений уравнений и неравенств с параметром Действительные числа. Математический диктант. 9 класс
Действительные числа. Математический диктант. 9 класс Древняя Греция. Числа правят миром
Древняя Греция. Числа правят миром Числові характеристики випадкових величин, показники варіації; первинна статистична обробка кількісних ознак
Числові характеристики випадкових величин, показники варіації; первинна статистична обробка кількісних ознак