Содержание
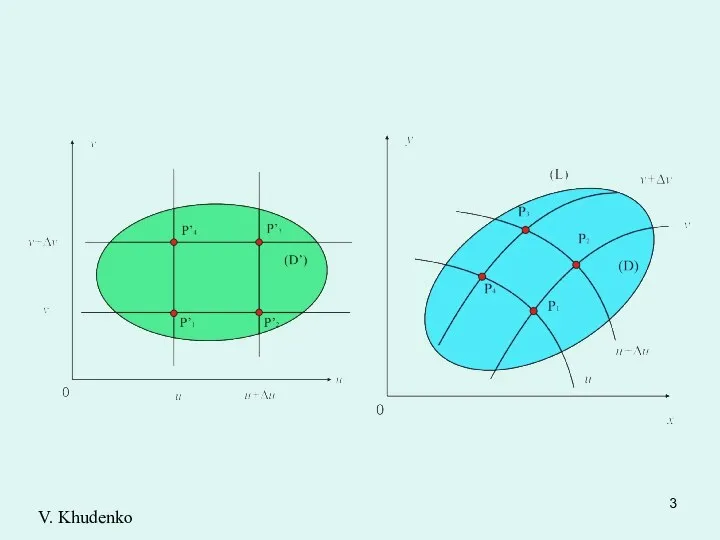
- 2. Замена переменных в двойном интеграле Пусть в плоскости Оху задана область (D), ограниченная линией (L). Предположим,
- 3. V. Khudenko
- 4. Разобьем область прямыми , на прямоугольные площадки. Тогда область (D) соответствующими кривыми линиями разобьется на криволинейные
- 5. Заменим приращения функций дифференциалами V. Khudenko
- 6. Полученные выражения дают основание считать четырехугольник параллелограммом со сторонами V. Khudenko
- 7. Введем обозначение Определитель I называется функциональным определителем функций и или якобианом . Имеет место равенство: Тогда
- 8. Замечание Переход к полярным координатам в двойном интеграле является частным случаем при u=r и v=φ. Тогда
- 9. Вычисление тройного интеграла в цилиндрических координатах Якобиан для случая трех переменных Формула замены переменных для тройного
- 10. В случае перехода к цилиндрическим координатам связь между декартовыми и цилиндрическими координатами: Тогда определитель Якоби V.
- 11. а формула замены переменных при переходе к цилиндрическим координатам примет вид V. Khudenko
- 13. Таким образом интеграл, после расстановки пределов интегрирования запишется в виде V. Khudenko
- 14. Пример Расставить пределы интегрирования в тройном интеграле и вычислить его значение в случае Область ограничена поверхностями:
- 17. Следовательно, область (V) задана неравенствами: Тогда С учетом того, что имеем V. Khudenko
- 18. Вычисление тройного интеграла в сферических координатах Положим u=ρ, v=φ, w=θ. Зависимость между декартовыми и сферическими координатами
- 19. формула замены переменных применительно к сферическим координатам примет вид V. Khudenko
- 21. Получаем формулу V. Khudenko
- 22. Пример Расставить пределы интегрирования в тройном интеграле, если область (V) представляет собой часть пространства. Ограниченную поверхностями
- 24. Уравнение сфер: ,тогда V. Khudenko
- 26. Скачать презентацию





















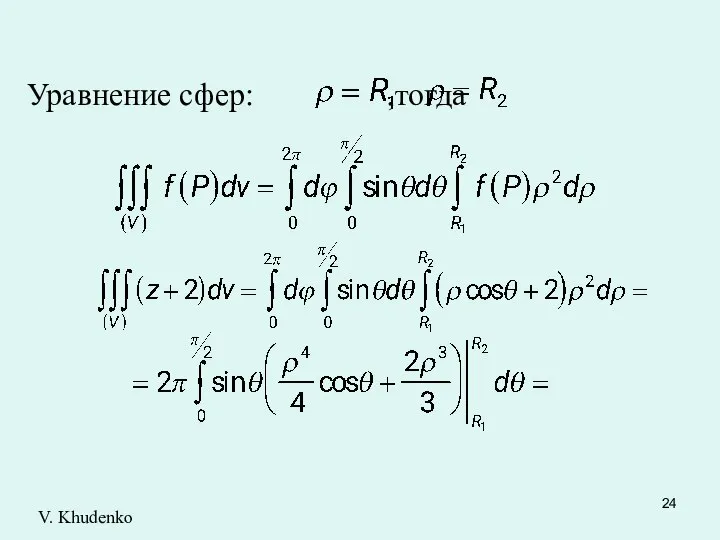
 Прямоугольник. Свойство прямоугольника
Прямоугольник. Свойство прямоугольника «ДАВАЙТЕ ПОЗНАКОМИМСЯ» КЛАССНЫЙ ЧАС
«ДАВАЙТЕ ПОЗНАКОМИМСЯ» КЛАССНЫЙ ЧАС Решение задач В1, ОГЭ
Решение задач В1, ОГЭ Решение тригонометрических уравнений (открытый урок в 10 классе)
Решение тригонометрических уравнений (открытый урок в 10 классе) Число 14. Многоугольники
Число 14. Многоугольники Векторы. 9 класс
Векторы. 9 класс ДЕЛИТЕЛИ И КРАТНЫЕ Математика – 6 Учитель математики МОУ «СОШ № 48» Бакреу Н.Н.
ДЕЛИТЕЛИ И КРАТНЫЕ Математика – 6 Учитель математики МОУ «СОШ № 48» Бакреу Н.Н. Современные средства обучения математике
Современные средства обучения математике Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс Система линейных уравнений с двумя переменными
Система линейных уравнений с двумя переменными Треугольник. Виды треугольников
Треугольник. Виды треугольников Длина окружности,
Длина окружности, Общая характеристика дисциплины
Общая характеристика дисциплины Рациональные числа Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»
Рациональные числа Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей» 1 класс. Математика. Знаки: «>» (больше), «<» (меньше)
1 класс. Математика. Знаки: «>» (больше), «<» (меньше) Реферат по математике на тему:
Реферат по математике на тему: Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель:
Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель:  Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Смешанные числа
Смешанные числа Коэффициенты слагаемых и упрощение выражений
Коэффициенты слагаемых и упрощение выражений Свойства прямоугольных треугольников. Решение задач
Свойства прямоугольных треугольников. Решение задач Основы теории фракталов
Основы теории фракталов Бесконечно убывающая геометрическая прогрессия. Фракталы
Бесконечно убывающая геометрическая прогрессия. Фракталы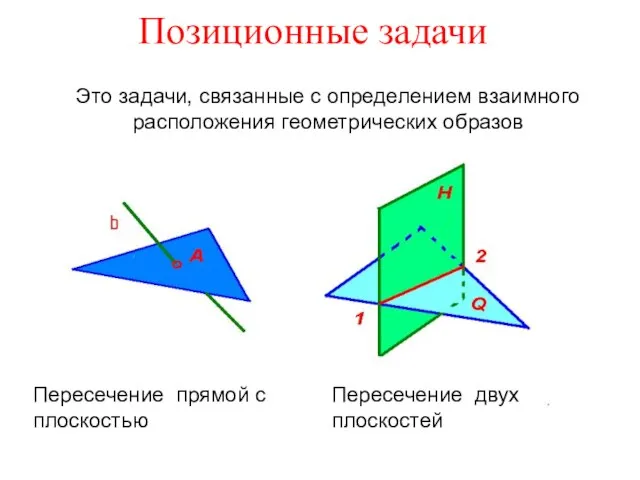 Позиционные задачи. Пересечение прямой с плоскостью. Пересечение двух плоскостей
Позиционные задачи. Пересечение прямой с плоскостью. Пересечение двух плоскостей Геометрия является самым могущественным средством для изощрения наших умственных способностей
Геометрия является самым могущественным средством для изощрения наших умственных способностей Элементы теории множеств
Элементы теории множеств Основы теории вероятности и математической статистики. Лекция 4
Основы теории вероятности и математической статистики. Лекция 4 Луч. Дополнительные лучи. 5 класс
Луч. Дополнительные лучи. 5 класс