Содержание
- 2. MODELOWANIE: POMYŚLMY O PROBLEMIE TROCHĘ WIĘCEJ Rozdział #3:
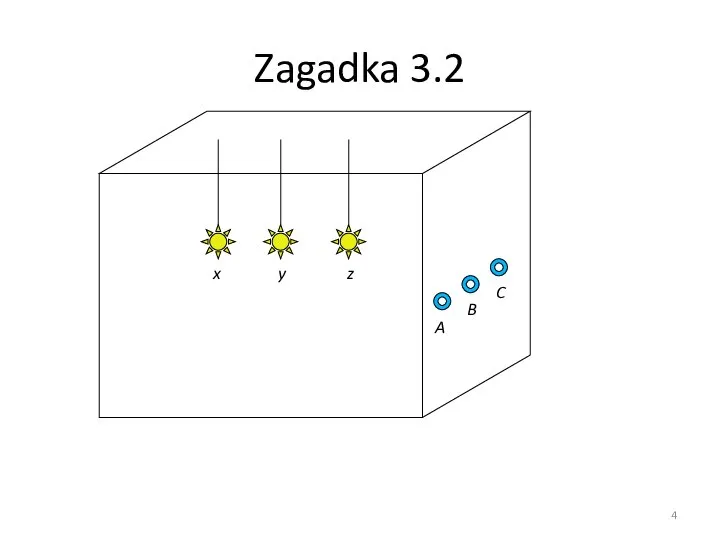
- 3. Zagadka 3.2 Stoisz przy drzwiach, prowadzących do pustego pokoju, w którym u sufitu wiszą trzy żarówki.
- 4. Zagadka 3.2 C B A x y z
- 5. Zagadka 3.2 Przełączniki: Możliwe ustawienia: A 1 1 1 1 0 0 0 0 B 1
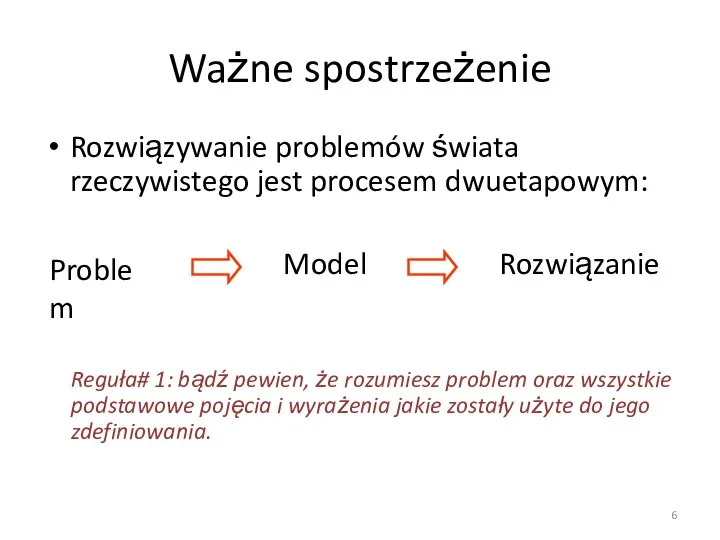
- 6. Ważne spostrzeżenie Rozwiązywanie problemów świata rzeczywistego jest procesem dwuetapowym: Reguła# 1: bądź pewien, że rozumiesz problem
- 7. Zagadka 3.3 Jest sobie podkowa z sześcioma otworami na gwoździe: Wykonaj dwa prostoliniowe cięcia, które podzielą
- 8. Reguła #3 Dokładne obliczenia i rozumowanie będą bardziej konstruktywne, jeśli zbudujesz model dla danego problemu, definiując
- 9. Zagadka 3.1 Pewne przedsiębiorstwo produkcyjne ma w ofercie tylko dwa produkty: krzesła i stoły. zysk ze
- 10. Zagadka 3.1 Pytanie brzmi: ile krzeseł i stołów powinna produkować firma, aby jej zysk był maksymalny?
- 11. Zagadka 3.1 Stosując regułę #3, możemy skonstruować model problemu, określając następujące jego elementy: Zmienne: są tylko
- 12. Zagadka 3.1 Cel: maksymalizacja wartości: 20$ x + 30$ y Np. jeśli firma będzie produkowała 10
- 13. Zagadka 3.1 Ograniczenia: wyprodukowanie krzesła wymaga jednej sztuki drewna i trzech roboczogodzin wyprodukowanie stołu wymaga sześciu
- 14. Zagadka 3.1 Model: formalny, matematyczny model zadania maksymalizacji zysku przedsiębiorstwa może być sformułowany następująco: maksymalizacja wartości:
- 15. Zagadka 3.1 Rozwiązanie: może to nie takie oczywiste na pierwszy rzut oka, ale… x = 18
- 16. Zagadka 3.1 Jednak przy rozwiązywaniu tego typu zadania zawsze należy sobie zadać dodatkowe pytania: Czy ten
- 17. Mapa – model świata rzeczywistego Weźmy „idealną” mapę dla dowolnego dużego miasta (mapa – model świata
- 18. Mapa – model świata rzeczywistego
- 19. Dobry model Dobry model – dostatecznie dokładny, aby wygenerować sensowne, konkretne rozwiązania, ale z drugiej strony
- 20. Model – kwestie do rozważenia Jak dokładny jest model (oceniając w ramach pojęć świata rzeczywistego, który
- 21. Krzesła i stoły Czy ten model dałoby się zastosować w świecie rzeczywistym? maksymalizacja wartości: 20$ x
- 22. Zagadka 3.4 Pani Brązowa obchodziła urodziny i jeden z gości zapytał ją o jej wiek. Pani
- 23. Zagadka 3.4 x: wiek pani Brązowej, y: wiek pana Brązowego Suma wieku pani Brązowej i pana
- 24. Zagadka 3.4 x: wiek Pani Brązowej, y: wiek Pana Brązowego y = 2(x – (y –
- 25. Obserwacja W 1579 François Viète zapoczątkował używanie symboli algebraicznych – x, y, z, etc. – do
- 26. Pieniądze i procenty Jan odziedziczył po zmarłym stryju 25% procent więcej pieniędzy niż jego siostra Julia.
- 27. Pieniądze i procenty Julia odziedziczyła x. Jan odziedziczył 1.25 x. Powinien dać jej 0.125 x tak,
- 28. Znaczenie modeli w życiu codziennym Znacznie mniej osób obawia się wypadku samochodowego niż ataku terrorystycznego. Tymczasem
- 29. Znaczenie modeli w życiu codziennym Prosty probabilistyczny model pozwoli zobaczyć te dane z innej perspektywy. Mamy
- 30. Znaczenie modeli w życiu codziennym Wiele osób nadinterpretowuje „niezwykłe” związki postaci: Krzysztof Kolumb odkrył Nowy Świat
- 31. Znaczenie modeli w życiu codziennym Proste modele mogą nas chronić przed tendencją do drastycznego niedoceniania częstości
- 32. Znaczenie modeli w życiu codziennym Zbudujmy prosty model. Załóżmy, że prawdopodobieństwo tzw. proroczego snu wynosi 1:10000.
- 33. Znaczenie modeli w życiu codziennym Prawdopodobieństwo wyśnienia jednego „nieproroczego” snu wynosi: 0.9999 Prawdopodobieństwo wyśnienia dwóch kolejnych
- 34. Znaczenie modeli w życiu codziennym Prawdopodobieństwo wyśnienia n „nieproroczych” snów wynosi: 0.9999n Jeżeli ktoś miewa sny
- 35. Znaczenie modeli w życiu codziennym Wniosek 2: Około 3.6% ludzi, którzy śnią każdej nocy, będzie miało
- 36. Znaczenie modeli w życiu codziennym Zbiegi okoliczności zdarzają się na świecie dużo częściej, niż wydaje się
- 37. Znaczenie modeli w życiu codziennym Kluczowa umiejętność: odróżnianie zdarzeń specyficznych od powszechnych. Jeżeli mamy koło (a
- 38. Znaczenie modeli w życiu codziennym Przykład: Sekwencja pierwszych liter nazw kolejnych miesięcy – w języku angielskim:
- 39. Znaczenie modeli w życiu codziennym Przykład: Sekwencja pierwszych liter nazw kolejnych miesięcy – w języku angielskim:
- 40. Znaczenie modeli w życiu codziennym Przykład: Sekwencja pierwszych liter nazw kolejnych miesięcy – w języku angielskim:
- 41. Znaczenie modeli w życiu codziennym Przykład: Sekwencja pierwszych liter nazw kolejnych miesięcy – w języku angielskim:
- 42. Znaczenie modeli w życiu codziennym Inny (pouczający) przykład… ☺ Jeden z przyjaciół Zygmunta Freuda, Wilhelm Fliess
- 43. Znaczenie modeli w życiu codziennym Fliess uważał, że dwie liczby 23 i 28 reprezentują długości takich
- 44. Znaczenie modeli w życiu codziennym Freud był pod tak wielkim wrażeniem tego odkrycia, że nie tylko
- 45. Pamiętaj o regule #3 Dokładne obliczenia i rozumowanie będą bardziej konstruktywne, jeśli zbudujesz model dla danego
- 46. Praca domowa #3a Cena biletu do parku rozrywki została obniżona; w rezultacie park odnotował 50-procentowy wzrost
- 47. Praca domowa #3b Abacki, Babacki i Cabacki postanowili we własnym gronie rozegrać zawody lekkoatletyczne. Było kilka
- 48. Zagadka 3.2 Stoisz przy drzwiach, prowadzących do pustego pokoju, w którym u sufitu wiszą trzy żarówki.
- 49. Zagadka 3.2 Rozwiązanie: wzbogacenie standardowego modelu (włączony/wyłączony) o czynnik temperatury! Ustawiamy dwa przełączniki (np. A i
- 50. Zagadka 3.3 Jest sobie podkowa z sześcioma otworami na gwoździe: Wykonaj dwa prostoliniowe cięcia, które podzielą
- 52. Скачать презентацию














































 Экспериментальная психология и статистика для психологов. (Лекция 2)
Экспериментальная психология и статистика для психологов. (Лекция 2) Чем опасно селфи
Чем опасно селфи Метод беседы
Метод беседы Основные положения неофрейдизма
Основные положения неофрейдизма Проблема выявления интернет-зависимости среди подростков
Проблема выявления интернет-зависимости среди подростков Целеполагание простыми словами. Как правильно мечтать
Целеполагание простыми словами. Как правильно мечтать Этика в документальном кино. Интервью. Событие. Режиссерский событийный ряд
Этика в документальном кино. Интервью. Событие. Режиссерский событийный ряд Ознакомление с эмоциями
Ознакомление с эмоциями Диагностика личностного потенциала взрослых и детей
Диагностика личностного потенциала взрослых и детей Зигмунд Фрейд – великий мыслитель
Зигмунд Фрейд – великий мыслитель Межличностные конфликты
Межличностные конфликты Семья как фактор риска отклоняющегося поведения
Семья как фактор риска отклоняющегося поведения Аттестационная работа. Организация исследовательской деятельности школьников с трудностями в обучении, работа педагога-психолога
Аттестационная работа. Организация исследовательской деятельности школьников с трудностями в обучении, работа педагога-психолога Детская тревожность
Детская тревожность Учет возрастных и индивидуальных особенностей детей дошкольного возраста при реализации ФГОС ДО
Учет возрастных и индивидуальных особенностей детей дошкольного возраста при реализации ФГОС ДО Наука как форма общественного сознания
Наука как форма общественного сознания Как защитить ребенка от кибербуллинга
Как защитить ребенка от кибербуллинга Тест Сакса Леви. Методика незаконченные предложения
Тест Сакса Леви. Методика незаконченные предложения Типология обществ
Типология обществ Mood Disorders
Mood Disorders Понятие групповой динамики. Динамические процессы в группе
Понятие групповой динамики. Динамические процессы в группе Поза, мимика, жесты как выражение позиции человека в процессе общения
Поза, мимика, жесты как выражение позиции человека в процессе общения Психология лиц с нарушением зрения
Психология лиц с нарушением зрения Диалог в работе: достижение и взаимопонимание
Диалог в работе: достижение и взаимопонимание Нейролінгвістичне програмування
Нейролінгвістичне програмування Сенсорные процессы у человека. Психологическая сущность ощущений. Тема 2
Сенсорные процессы у человека. Психологическая сущность ощущений. Тема 2 Использование техники постановки вопросов
Использование техники постановки вопросов Детерминация и самодетерминация личности
Детерминация и самодетерминация личности