Содержание
- 2. ЧТО ТАКОЕ МНОГОЧЛЕН? Многочленом с переменной х (или от переменной х), называют сумму степеней переменной х
- 3. Многочлен Р(х) делится на многочлен Q(х)≠0, если Р(х)=Q(x)∙M(x), где М(х) – некоторый многочлен.
- 4. Свойства делимости многочленов «столбиком»:
- 5. 1 свойство: Если многочлен Pn(x) делится на многочлен Qk(x), а многочлен Qk(x) делится на многочлен Mm(x),
- 6. 2 свойство: Если многочлены Рn(х) и Qn(x) делятся на многочлен Mk (x), то многочлены Рn(х)+Qn(x) и
- 7. 3 свойство: Если P(x) делится на Q(x), то всякий корень Q(x) является корнем P(x). Действительно если
- 8. Алгоритм деления многочленов «столбиком» Расположить делимое и делитель в убывающих степенях х; Разделить старший член делимого
- 9. Разделить уголком многочлен P(x)=10х2-7х-12 на многочлен Q(x)=5х+4. Решение. делимое _ 10х2-7х-12 5х+4 делитель 10х2+8х 2х-3 частное
- 10. Разделить многочлен P(x)=3х4+2х2-1 на многочлен Q(x)=х2+х. Решение. _3х4 +2х2-1 х2+х 3х4+3х2 3х2-3х+5 _-3х3+2х2-1 -3х3 -3х2 _5х2-
- 11. Задача 2п2 -11п+13 При каких натуральных значениях п выражение п-3 является целым числом? Решение. Разделим числитель
- 12. Степень частного равна разности степеней делимого и делителя, а степень остатка всегда меньше степени делителя.
- 13. Алгоритм вычислений по схеме Горнера:
- 14. 1 шаг. Под первым коэффициентом делимого а0 пишется ещё раз этот коэффициент. 2 шаг. Под коэффициентом
- 15. 3 шаг. Под коэффициентом а2 пишется число b2= b1b+а2. 4 шаг. Под коэффициентом а3 пишется число
- 16. Для любого многочлена Р(х)=а0хп+а1хп-1+…+ап-1х+ап и любого числа с можно написать разложение Р(х) по степеням разности х-с:
- 17. Разложить многочлен Р(х)=х4-5х3-3х2+9 по степеням разности х-3. Решение. Выполним деление по схеме Горнера: Таким образом, Р(х)=(х-3)4+7(х-3)3+6(х-3)2-45(х-3)-72.
- 18. Теорема Безу
- 19. Определение. Остаток от деления многочлена Р(х) на двучлен х-а равен значению этого многочлена при х=а: Р(а)=R.
- 20. Следствие №1. Если х=а – корень уравнения Рп(х)=0, то R=0 и многочлен Рп(х) делится нацело на
- 21. Задача Выяснить, делится ли нацело многочлен Р(х)=х100+3х79+х48-х27 на х+1. Решение. Остаток от деления Р(х) на х+1
- 23. Скачать презентацию




















 Инструкция по работе с интернет-магазином «Клякса»
Инструкция по работе с интернет-магазином «Клякса» Цивилизованное лоббирование 1.Лоббизм:суть, легитимность, практика 2.Методы лоббирования 3.Лоббирование законодательного пр
Цивилизованное лоббирование 1.Лоббизм:суть, легитимность, практика 2.Методы лоббирования 3.Лоббирование законодательного пр ИНТЕРМОДАЛЬНЫЕ ПЕРЕВОЗКИ ГРУЗОВ Контейнерные перевозки грузов; Операторы смешанной перевозки грузов; Особенности взаимодей
ИНТЕРМОДАЛЬНЫЕ ПЕРЕВОЗКИ ГРУЗОВ Контейнерные перевозки грузов; Операторы смешанной перевозки грузов; Особенности взаимодей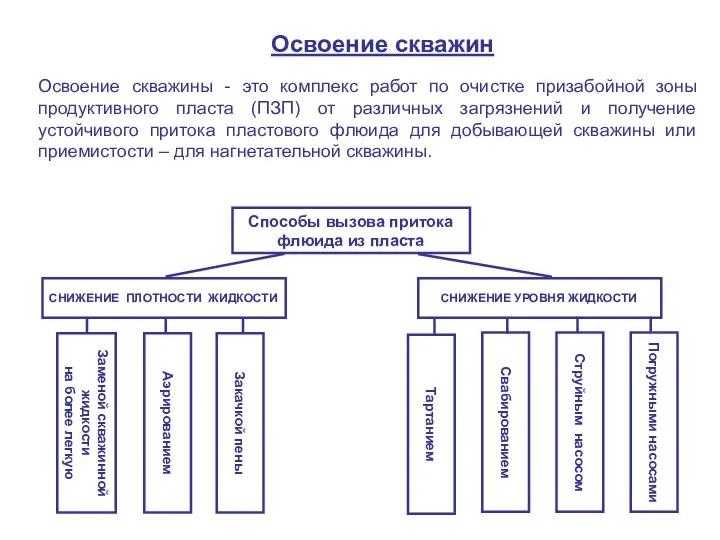 ОСВОЕНИЕ СКВАЖИН
ОСВОЕНИЕ СКВАЖИН  Тема урока: Современная политическая карта мира. Классификация и типология стран.
Тема урока: Современная политическая карта мира. Классификация и типология стран.  Экскурсионная программа для школьников. Парк «Ключи»
Экскурсионная программа для школьников. Парк «Ключи» Презентация Организация страховой деятельности и ее нормативно-правовая база
Презентация Организация страховой деятельности и ее нормативно-правовая база Типовые структуры ВИС
Типовые структуры ВИС Титаны возрождения
Титаны возрождения Основной математический аппарат
Основной математический аппарат Паттерны = Шаблоны проектирования
Паттерны = Шаблоны проектирования Традиции и ритуалы дня благодарения
Традиции и ритуалы дня благодарения Русская Масленица
Русская Масленица Физическое воспитание дошкольников
Физическое воспитание дошкольников Проектирование деревообрабатывающего оборудования и инструмента. Схемы машин
Проектирование деревообрабатывающего оборудования и инструмента. Схемы машин Архитектура русского и украинского барокко
Архитектура русского и украинского барокко Микроконтроллеры ATMEL AVR. Общие принципы работы микропроцессорной системы
Микроконтроллеры ATMEL AVR. Общие принципы работы микропроцессорной системы ПРАВОВЫЕ АКТЫ ОЦЕНОЧНОЙ ДЕЯТЕЛЬНОСТИ
ПРАВОВЫЕ АКТЫ ОЦЕНОЧНОЙ ДЕЯТЕЛЬНОСТИ день цифры 8 - презентация для начальной школы
день цифры 8 - презентация для начальной школы Презентация Крепежные изделия
Презентация Крепежные изделия Презентация "Введение в менеджмент" - скачать презентации по Экономике
Презентация "Введение в менеджмент" - скачать презентации по Экономике Перинатальная охрана плода и новорожденного Казанский государственный медицинский университет Кафедра акушерства и гинекол
Перинатальная охрана плода и новорожденного Казанский государственный медицинский университет Кафедра акушерства и гинекол Введение в SEO
Введение в SEO Meine Traumschule
Meine Traumschule Как стать бухгалтером с нуля. Программа вебинара
Как стать бухгалтером с нуля. Программа вебинара Определить индексы заработной платы переменного состава
Определить индексы заработной платы переменного состава Школа для развития своего таланта. Проект
Школа для развития своего таланта. Проект Методология проведения медико-социологических исследований
Методология проведения медико-социологических исследований