Содержание
- 2. Математическая статистика - наука, выявляющая закономерности повторяющихся случайных явлений на основе обработки статистических данных, полученных в
- 3. Основные задачи мат. статистики: 1. Разработка методов анализа наблюдаемых случайных данных ( оценка неизвестной вероятности события,
- 4. Определения. Генеральная совокупность – все множество имеющихся наблюдений или объектов, относящихся к изучаемому явлению.
- 5. Выборка – набор наблюдений или объектов, случайно отобранных из генеральной совокупности. Объем генеральной совокупности N и
- 6. Виды выборки Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность; Бесповторная –
- 7. NB! Выборка должна быть репрезентативной (представительной).
- 8. Пусть с.в. Х принимает в выборке значение х1 n1 раз, х2 – n2 раз, …, хк
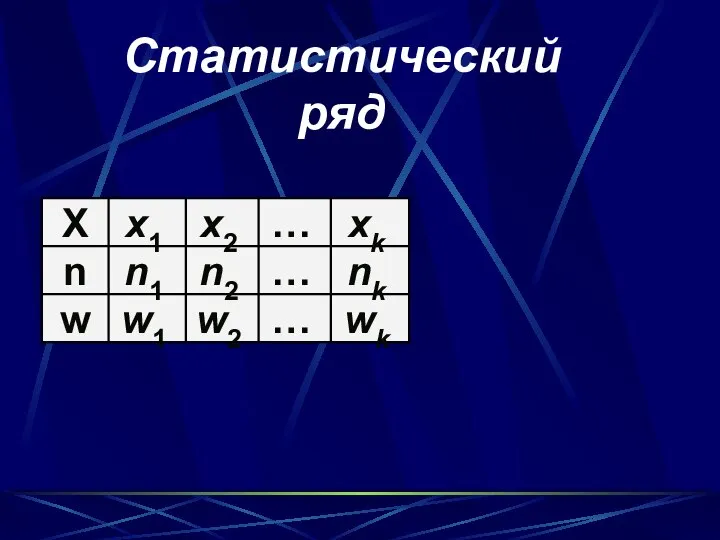
- 9. Статистический ряд
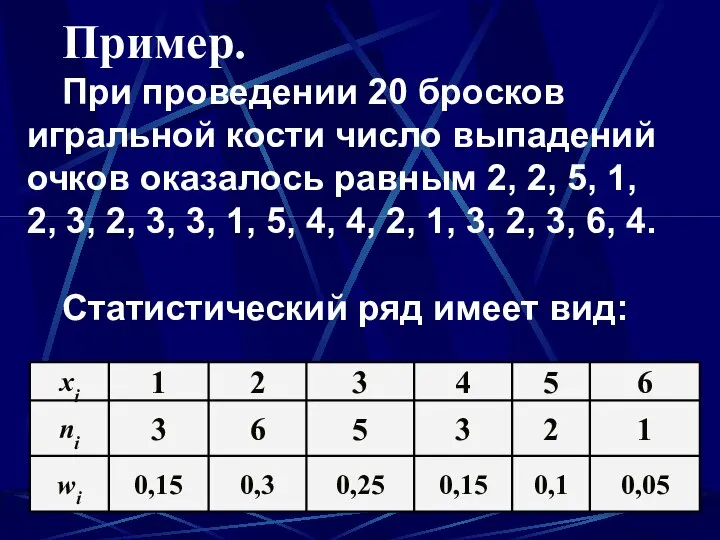
- 10. Пример. При проведении 20 бросков игральной кости число выпадений очков оказалось равным 2, 2, 5, 1,
- 11. Определение. Последовательность наблюдений, записанных в порядке возрастания или убывания х(1), х(2),…, х(к): х(1) х(1), х(2),…, х(к):
- 12. Определение. Наблюдения, образующие вариационный ряд х(1), х(2),…, х(к), называются порядковыми статистиками, а их номера в вариационном
- 13. ВОПРОС 30: Группированные данные
- 14. Статистический ряд для непрерывной с.в.
- 15. Полигон частот: ломаная, отрезки которой соединяют точки с координатами (x1, p1*), (x2, p2*),…, (xk, pk*) x
- 16. Выборочная функция распределения и гистограмма ВОПРОС 31:
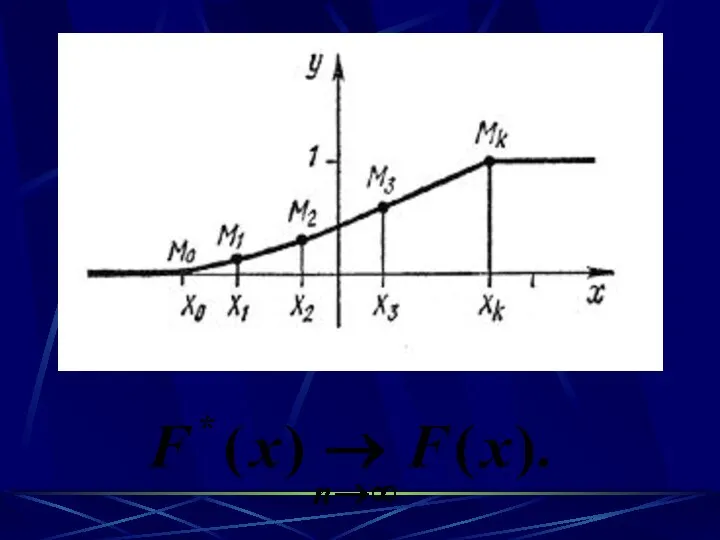
- 17. Определение. Выборочной (эмпирической) функцией распределения называют функцию F*(x), определяющую для каждого значения х относительную частоту события
- 20. Свойства F*(x) (совпадают со свойствами F(x)): 1. 0 ≤ F*(x) ≤ 1. 2. F*(x) – неубывающая
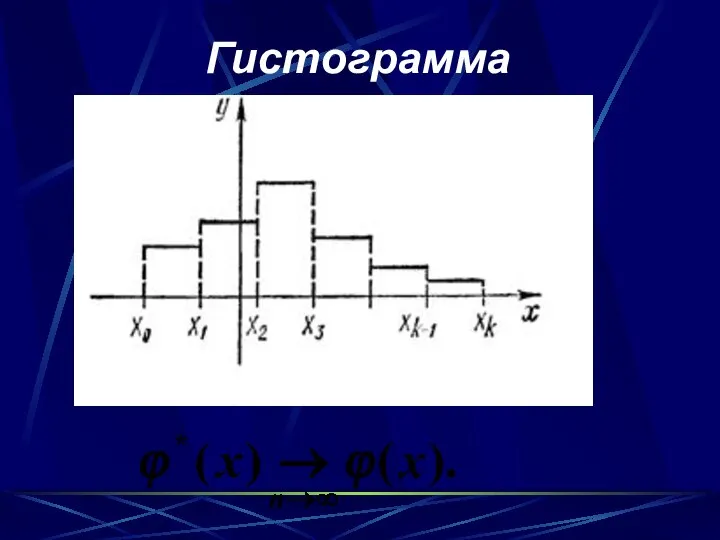
- 21. Эмпирическая плотность распределения которая в интервале ( Xi-1, Xi ] постоянна и равна
- 22. Гистограмма
- 23. ВОПРОС 32: Оценки параметра положения: выборочное среднее, оценки моды и медианы
- 24. ОПРЕДЕЛЕНИЯ. Выборочное среднее:
- 25. Мода: Медиана:
- 26. ВОПРОС 33: Оценки параметра масштаба: оценки дисперсии, начальных и центральных моментов
- 27. ОПРЕДЕЛЕНИЯ. Выборочной дисперсией называется
- 28. Центральный эмпирический момент: Начальный эмпирический момент:
- 29. Пример 1. Найти числовые характеристики выборки
- 31. ВОПРОС 34: Свойства оценок
- 32. Схема: k выборок одного и того же объема n и вычислим для каждой из них оценку
- 34. Определение. Оценка некоторого признака называется АСИМПТОТИЧЕСКИ НЕСМЕЩЕННОЙ, если для выборки х1, х2, …, хп
- 35. Определение. Статистическая оценка называется ЭФФЕКТИВНОЙ, если она при заданном объеме выборки n имеет наименьшую возможную дисперсию
- 36. Определение. СОСТОЯТЕЛЬНОЙ называется статистическая оценка, которая при стремится по вероятности к оцениваемому параметру :
- 37. Теорема. Выборочное среднее представляет собой несмещенную оценку математического ожидания E(Х). Доказать самостоятельно!
- 38. Выборочное дисперсия представляет собой смещенную оценку дисперсии:
- 39. Исправленная выборочная дисперсия:
- 40. Исправленное среднее квадратическое отклонение
- 41. Определение. Оценка некоторого признака называется асимптотически несмещенной, если для выборки х1, х2, …, хn
- 42. СПОСОБЫ ПОСТРОЕНИЯ ОЦЕНОК
- 43. ВОПРОС 35: Метод максимального правдоподобия
- 44. Модель. ] Х – дискретная с.в., которая в результате п испытаний приняла значения х1, х2, …,
- 45. Определение. Назовем функцией правдоподобия дискретной случайной величины Х функцию аргумента Θ, определяемую по формуле: L (х1,
- 46. Определение. Оценкой наибольшего правдоподобия называется оценка при котором функция правдоподобия достигает максимума: ln L – логарифмическая
- 47. Алгоритм поиска ММП-оценки: ММП-оценки состоятельны (хотя могут быть смещенными), распределены асимптотически нормально и имеют наименьшую дисперсию
- 48. ВОПРОС 36: Метод моментов
- 49. ] известный вид п.р. f(x, Θ1, Θ2 ) определяется двумя неизвестными параметрами Θ1 и Θ2. Требуется
- 50. ВОПРОС 37: Метод наименьших квадратов
- 51. …)
- 52. Пример: y=ax+b
- 54. ВОПРОС 38: Байесовский подход к получению оценок
- 55. ](Y, X) – случайный вектор, для которого известна плотность р(Y|x) . Для оценки некоторой заданной функции
- 56. ДВУМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
- 57. ВОПРОС 39: Двумерные случайные величины
- 58. Определение. Двумерной случайной величиной называют систему из двух случайных величин для которой определена вероятность совместного выполнения
- 59. Определение. Функция двух переменных определенная для любых x и y, называется функцией распределения системы двух случайных
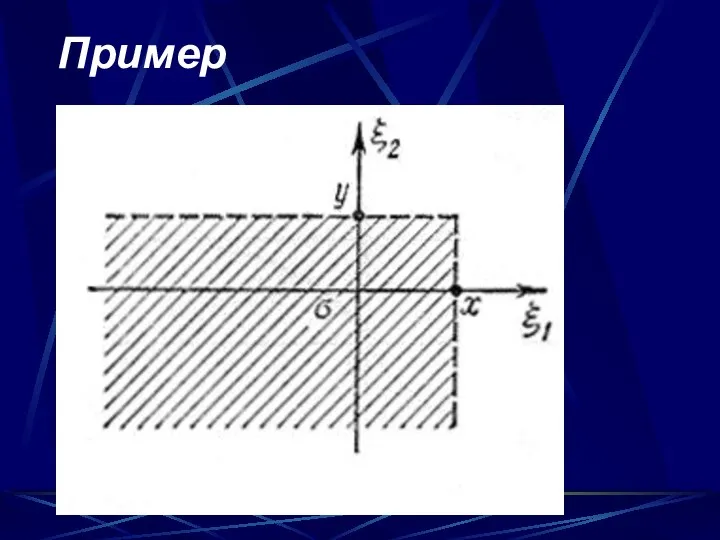
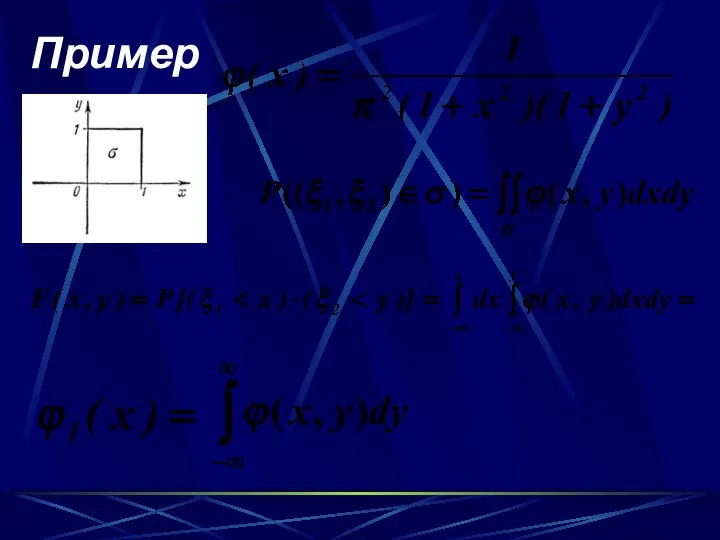
- 60. Пример
- 61. ДИСКРЕТНАЯ ДВУМЕРНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА Определение. Двумерная случайная величина называется дискретной, если - дискретные величины.
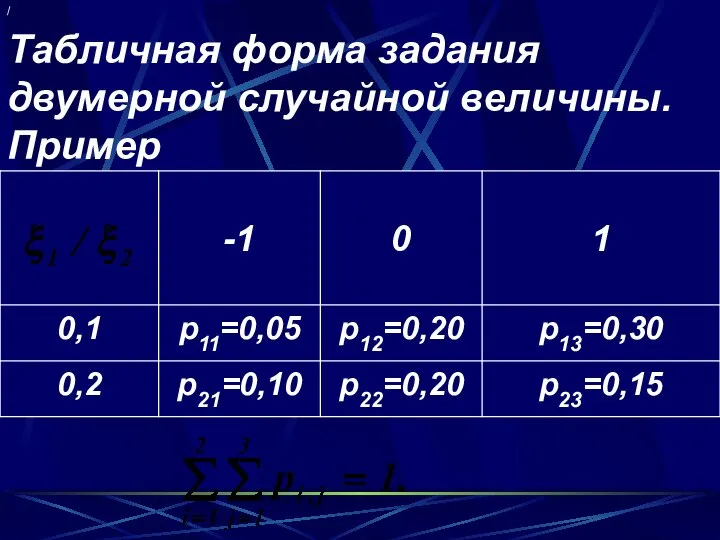
- 63. Табличная форма задания двумерной случайной величины. Пример /
- 64. Определение. Две дискретные случайные величины называются независимыми, если
- 65. Пример.
- 66. НЕПРЕРЫВНАЯ ДВУМЕРНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА Определение. Двумерная случайная величина называется непрерывной, если
- 67. Определение. Функция называется плотностью распределения вероятностей системы двух величин
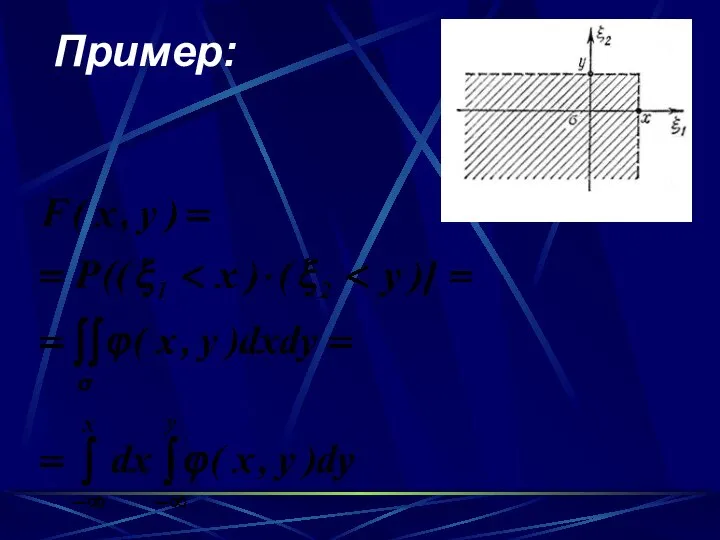
- 68. Пример:
- 70. Для независимых с.в.
- 72. Отсюда
- 73. Аналогично:
- 74. Пример
- 75. Определение. Двумерная случайная величина распределена нормально, если плотность распределения системы имеет вид:
- 76. Для независимых с.в.
- 77. ВОПРОС 40: Числовые характеристики двумерных случайных величин
- 78. Определение. Начальным моментом порядка (k, s) двумерной случайной величины (Х, Y) называется
- 79. Определение. Центральным моментом порядка (k, s) двумерной случайной величины (Х, Y) называется
- 80. При этом E(Х) = α1,0, E(Y) = α0,1, D(X) = μ2,0, D(Y) = μ0,2.
- 81. ВОПРОС 41: Корреляционный момент и коэффициент корреляции
- 82. Определение. Корреляционным моментом системы двух случайных величин называется второй смешанный центральный момент Kxy = μ1,1 =
- 84. Безразмерной характеристикой коррелированности двух случайных величин является коэффициент корреляции Определение.
- 85. Для независимых Х и Y f(x =f1(x)f2(y), тогда Теорема.
- 86. Доказательство
- 87. ВОПРОС 44: Статистическое описание и вычисление характеристик двумерного случайного вектора
- 88. Двумерная выборка представляет собой набор значений случайного вектора: (х1, у1), (х2, у2), …, (хn, уn). Дескриптивный
- 90. Скачать презентацию














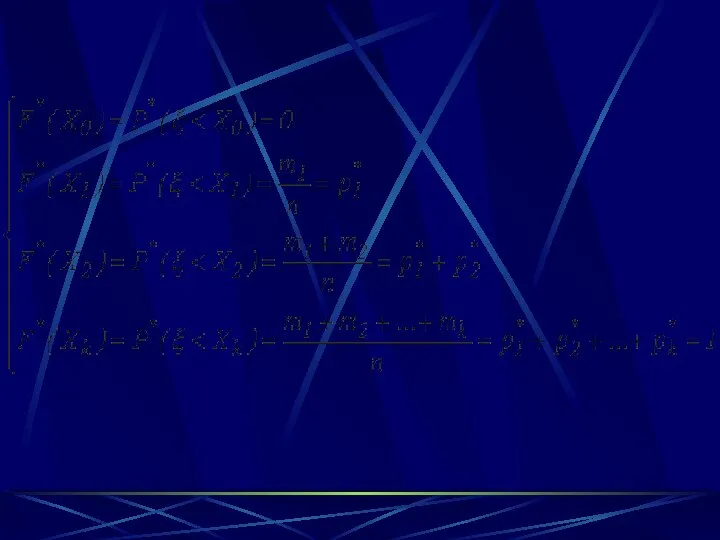

![Эмпирическая плотность распределения которая в интервале ( Xi-1, Xi ] постоянна и равна](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301233/slide-20.jpg)





















![Модель. ] Х – дискретная с.в., которая в результате п испытаний](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301233/slide-43.jpg)




![] известный вид п.р. f(x, Θ1, Θ2 ) определяется двумя неизвестными](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301233/slide-48.jpg)

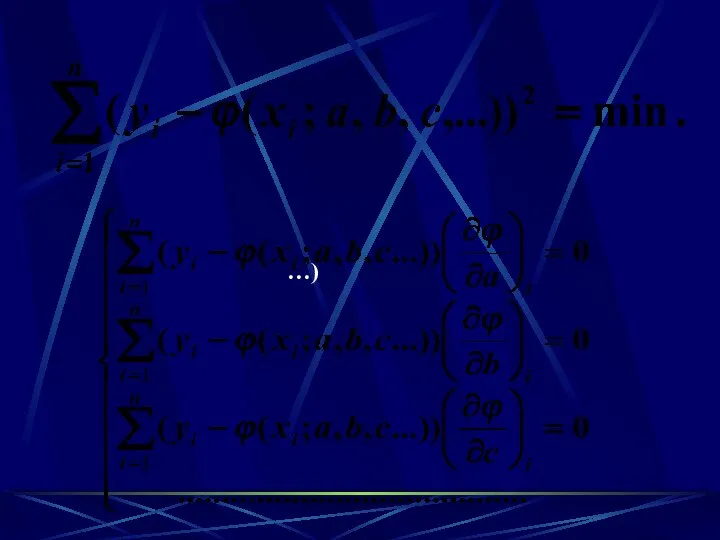

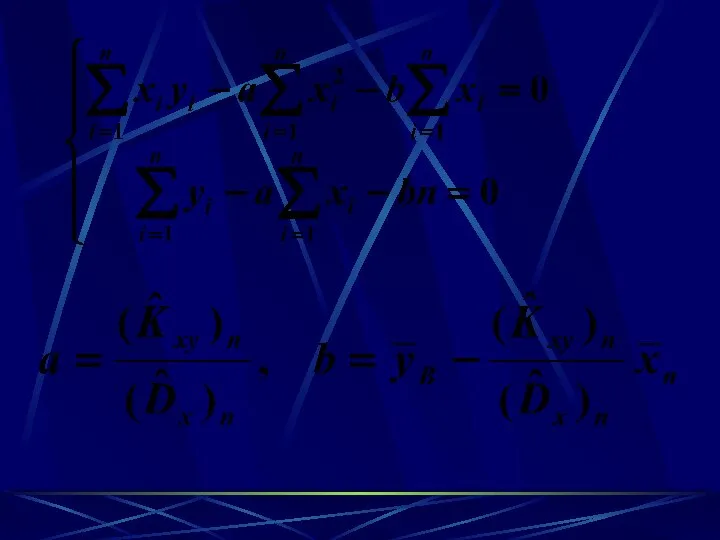

 – случайный вектор, для которого известна плотность р(Y|x) .](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301233/slide-54.jpg)





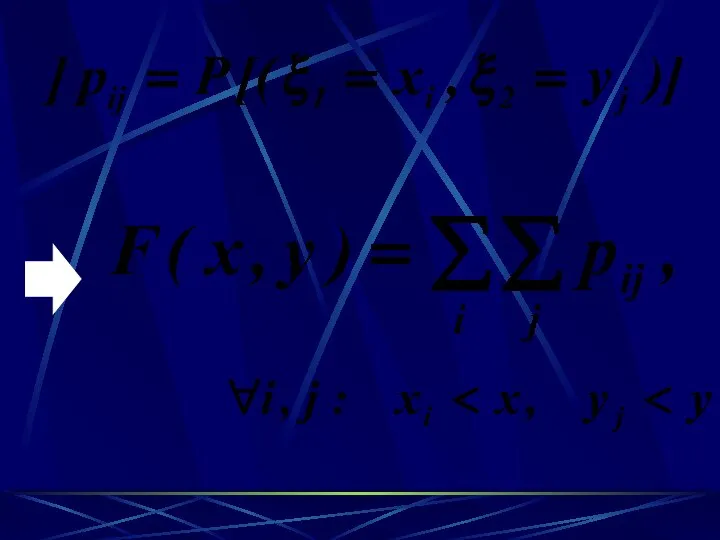







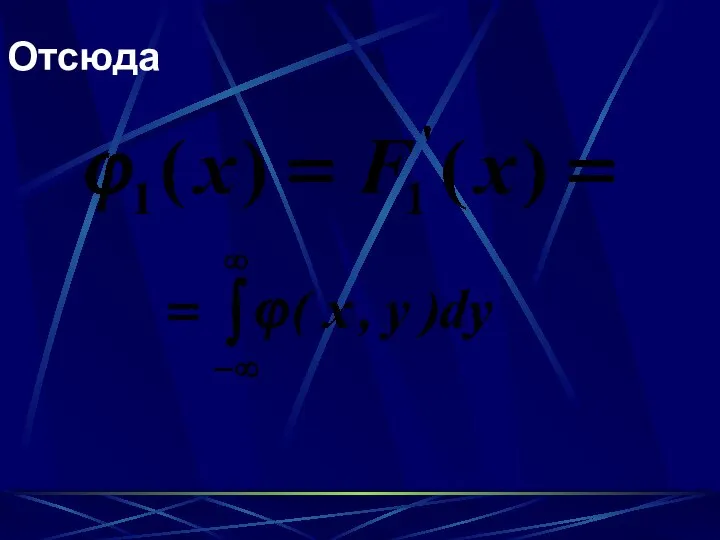






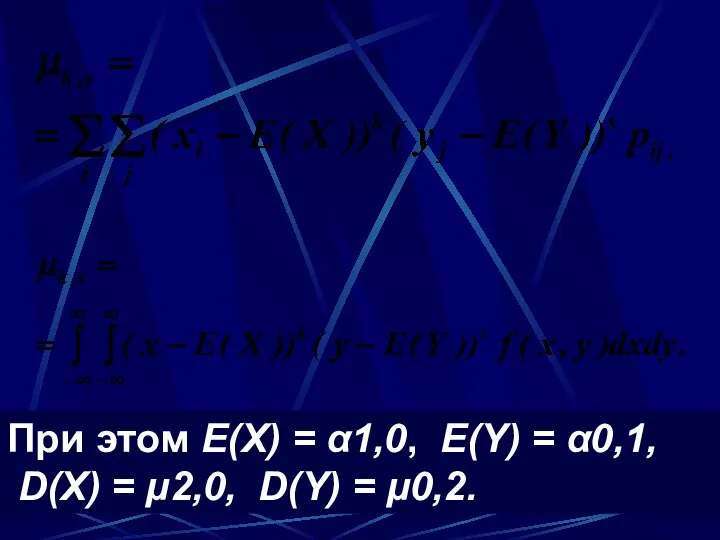


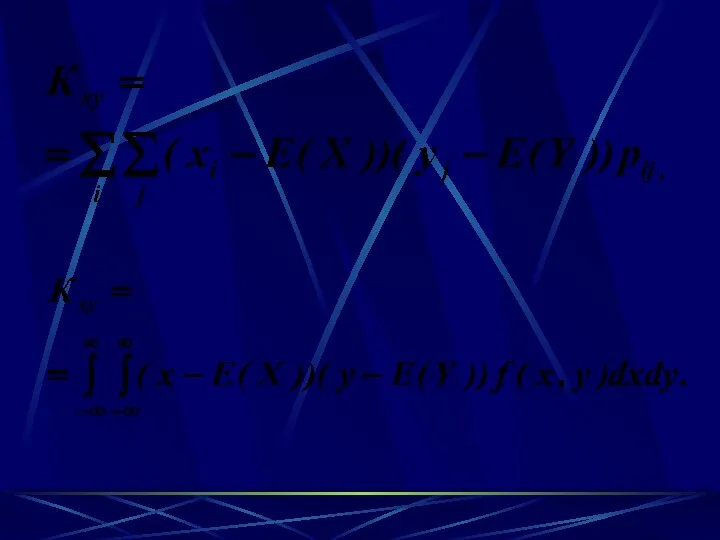





 Исследование проблем развития хостелов и иных бюджетных средств размещения в Тюмени и способы их решения»
Исследование проблем развития хостелов и иных бюджетных средств размещения в Тюмени и способы их решения» Презентация "Формирование толерантного сознания на уроках МХК" - скачать презентации по МХК
Презентация "Формирование толерантного сознания на уроках МХК" - скачать презентации по МХК Виды плоттеров и их технические характеристики
Виды плоттеров и их технические характеристики Каролина 1532 г
Каролина 1532 г Авиационные машины постоянного тока (генераторы)
Авиационные машины постоянного тока (генераторы) Использование здоровьесберегающих технологий на уроках биологии и во внеурочное время Учитель биологии МОУ «Краснослободская
Использование здоровьесберегающих технологий на уроках биологии и во внеурочное время Учитель биологии МОУ «Краснослободская  Циклический вычислительный процесс. (Лабораторная работа 4)
Циклический вычислительный процесс. (Лабораторная работа 4) Принципы современного менеджмента
Принципы современного менеджмента Масленица
Масленица Рубежно – зачетная работа по системам компьютерной графики
Рубежно – зачетная работа по системам компьютерной графики  Гонорея
Гонорея Оказание первой медицинской помощи при тепловом и солнечном ударе, обморожении и ожоге
Оказание первой медицинской помощи при тепловом и солнечном ударе, обморожении и ожоге Исторические этапы научной картины мира Подготовили студентки 1 курса группы э122б Гавриленко Екатерина и Гуторова Анна
Исторические этапы научной картины мира Подготовили студентки 1 курса группы э122б Гавриленко Екатерина и Гуторова Анна Программа для преобразования воксельной модели в полигональную
Программа для преобразования воксельной модели в полигональную Паттерны в программировании
Паттерны в программировании ПЯВУ. Основы программирования. Лекция 14. Решение системы уравнений методом Гаусса. Вычисление числа Пи методом “МонтеКарло”
ПЯВУ. Основы программирования. Лекция 14. Решение системы уравнений методом Гаусса. Вычисление числа Пи методом “МонтеКарло” Основы рекламы: типология (классификация видов рекламы)
Основы рекламы: типология (классификация видов рекламы) Первый опыт работы Лузского школьного округа Пелевин Л.В., директор КОГОАУ СОШ г.Лузы 2012 год
Первый опыт работы Лузского школьного округа Пелевин Л.В., директор КОГОАУ СОШ г.Лузы 2012 год Логические функции
Логические функции  Ответственность родителей за правонарушения детей подросткового возраста
Ответственность родителей за правонарушения детей подросткового возраста Презентация на тему "Здоровьесберегающие технологии, как ресурс здоровьесберегающей образовательной среды" - скачать презен
Презентация на тему "Здоровьесберегающие технологии, как ресурс здоровьесберегающей образовательной среды" - скачать презен Презентация Цыганская Культура
Презентация Цыганская Культура Бюджетный процесс
Бюджетный процесс  Строительная акустика. Область слышимости. Уровень звукового давления. Громкость. Измерение и оценка шума
Строительная акустика. Область слышимости. Уровень звукового давления. Громкость. Измерение и оценка шума Дресс-код для школы
Дресс-код для школы Процессы газообмена
Процессы газообмена Tradition korean food
Tradition korean food Презентация Таможенная ревизия
Презентация Таможенная ревизия