Содержание
- 2. Основи Теорії Ігор Теорія Прийняття рішень © ЄА. Лавров, 2014-2019 /30
- 3. Теорія Ігор Теорія Прийняття рішень © ЄА. Лавров, 2014-2019 /14
- 4. Лекція 7. Основні поняття Теорії ІГОР Зміст лекції: 1. Теорія ігор .Проблема Прийняття рішень в умовах
- 5. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 1.Теорія ігор .Проблема Прийняття рішень в умовах
- 6. Теорія ігор .Проблема Прийняття рішень в умовах конфлікту В теорії ігор розглядаються ситуації, пов'язані з прийняттям
- 7. Теорія ігор .Проблема Прийняття рішень в умовах конфлікту В ігровому конфлікті беруть участь два противника, іменовані
- 8. Теорія ігор .Проблема Прийняття рішень в умовах конфлікту При позначенні гравців через А і В з
- 9. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 2.Оптимальне рішення гри двох осіб з нульовою
- 10. 2. Оптимальне рішення гри двох осіб з нульовою сумою Оскільки гри беруть свій початок в конфлікті
- 11. 2. Оптимальне рішення гри двох осіб з нульовою сумою Приклад 1 . Дві компанії А і
- 12. 2. Оптимальне рішення гри двох осіб з нульовою сумою Приклад 1 продовження. Залежно від уміння й
- 13. 2. Оптимальне рішення гри двох осіб з нульовою сумою. Приклад 1. продовження Аналіз стратегій комп. А.
- 14. 2. Оптимальне рішення гри двох осіб з нульовою сумою. Приклад1.продовження Аналіз стратегій комп. B. Так як
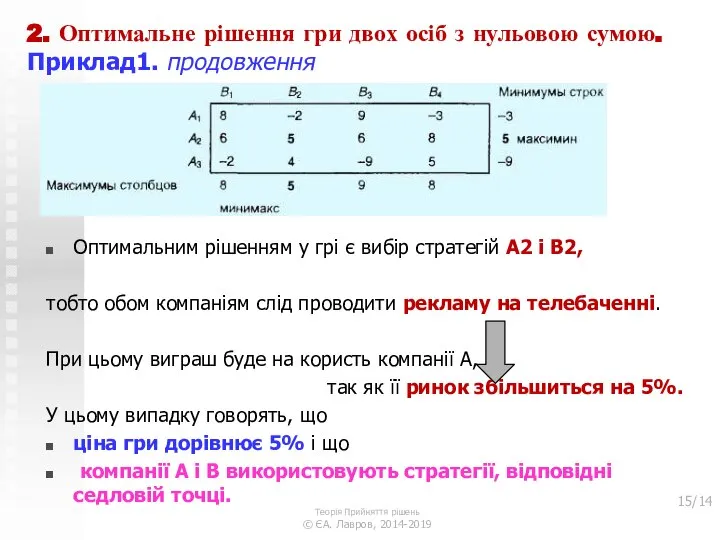
- 15. 2. Оптимальне рішення гри двох осіб з нульовою сумою. Приклад1. продовження Оптимальним рішенням у грі є
- 16. 2. Оптимальне рішення гри двох осіб з нульовою сумою. Приклад 1. продовження Рішення, що відповідає сідловой
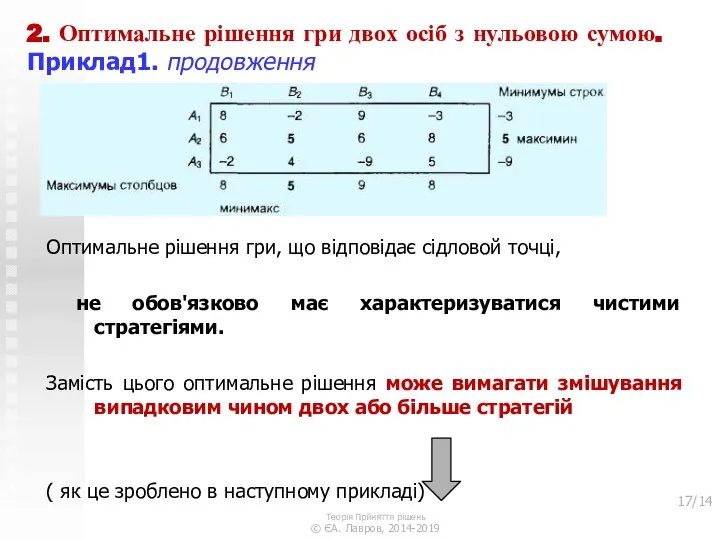
- 17. 2. Оптимальне рішення гри двох осіб з нульовою сумою. Приклад1. продовження Оптимальне рішення гри, що відповідає
- 18. 2. Оптимальне рішення гри двох осіб з нульовою сумою. Приклад2. Два гравці A і В грають
- 19. 2. Приклад2. Максиміна і мінімаксна величини (ціни) для цієї гри дорівнюють -1 дол. і 1 дол.
- 20. 2. Приклад2. Постійна спокуса кожного гравця перейти до іншої стратегії вказує на те, що рішення у
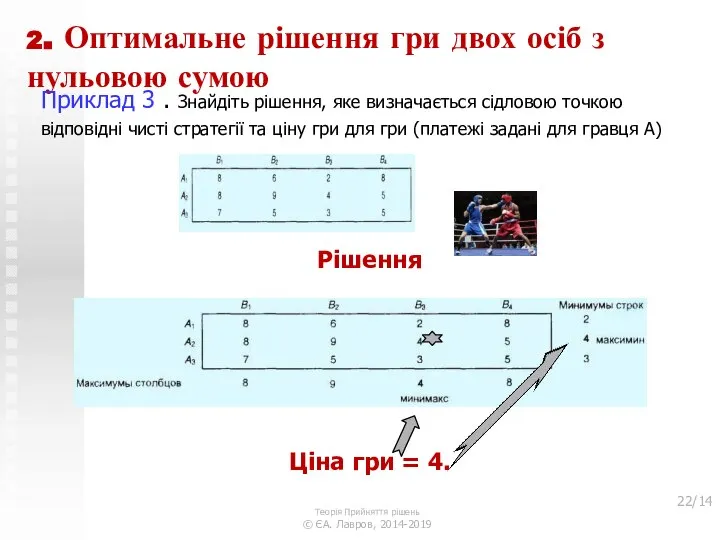
- 21. 2. Оптимальне рішення гри двох осіб з нульовою сумою Приклад 3 . Знайдіть рішення, яке визначається
- 22. 2. Оптимальне рішення гри двох осіб з нульовою сумою Приклад 3 . Знайдіть рішення, яке визначається
- 23. 2. Оптимальне рішення гри двох осіб з нульовою сумою Приклад 3 . Знайдіть рішення, яке визначається
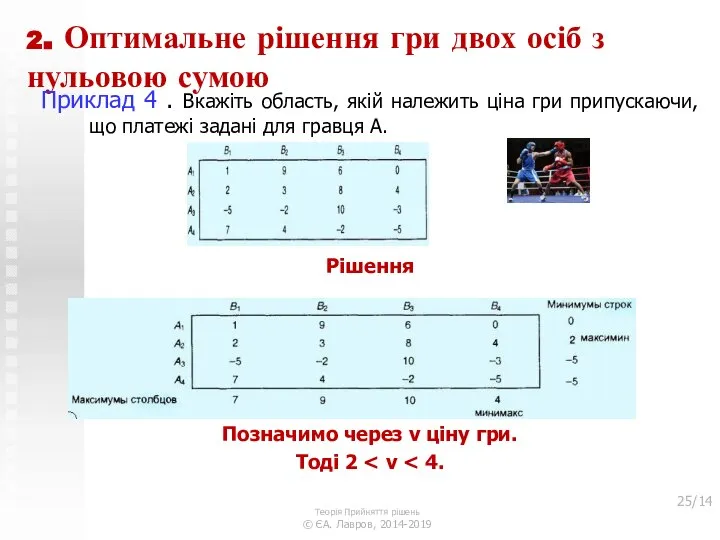
- 24. 2. Оптимальне рішення гри двох осіб з нульовою сумою Приклад 4 . Вкажіть область, якій належить
- 25. 2. Оптимальне рішення гри двох осіб з нульовою сумою Приклад 4 . Вкажіть область, якій належить
- 26. 3.Рішення матричних ігор у змішаних стратегіях Теорія Прийняття рішень © ЄА. Лавров, 2014-2019 /14
- 27. 3Рішення матричних ігор у змішаних стратегіях Може бути знайдено графічно, або методами лінійного програмування. Графічний метод
- 28. 3Рішення матричних ігор у змішаних стратегіях. Постановка задачі Розглянемо гру 2 х n, в якій гравець
- 29. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20 Рассмотрим следующую игру 2x4, в которой платежи
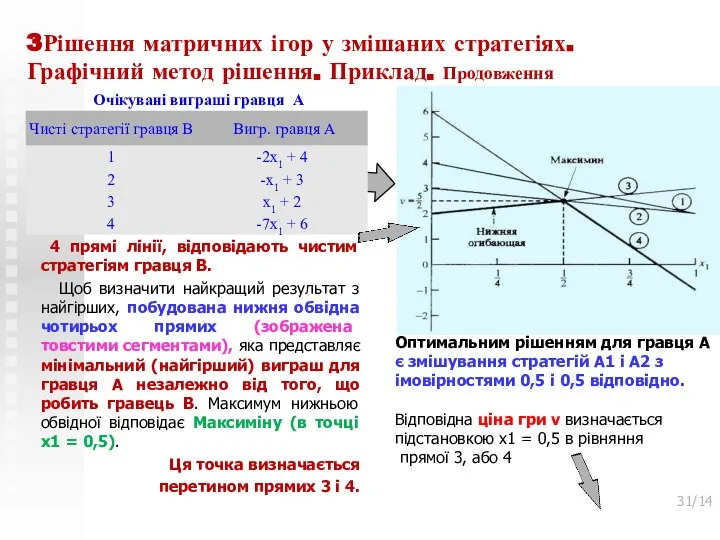
- 30. 3Рішення матричних ігор у змішаних стратегіях. Графічний метод рішення. Приклад. Рассмотрим следующую игру 2x4, в которой
- 31. 3Рішення матричних ігор у змішаних стратегіях. Графічний метод рішення. Приклад. Продовження 4 прямі лінії, відповідають чистим
- 32. 3Рішення матричних ігор у змішаних стратегіях. Графічний метод рішення. Приклад. Продовження Оптимальна змішана стратегія гравця В
- 33. 3Рішення матричних ігор у змішаних стратегіях. Графічний метод рішення. Приклад. Продовження Результат Рішення гри для гравця
- 34. 4. Рішення матричних ігор методами лінійного програмування Теорія Прийняття рішень © ЄА. Лавров, 2014-2019 /100
- 35. 4. Рішення матричних ігор методами лінійного програмування Теорія ігор знаходиться в тісному зв'язку з лінійним програмуванням,
- 36. 4. Рішення матричних ігор методами лінійного програмування Оптимальні значення ймовірностей xi, i = 1, 2, ...,
- 37. Довідка Джон фон Нейман . англ. John von Neumann), Нейман Янош Лайош (угор. Neumann János Lajos),
- 38. 4. Рішення матричних ігор методами лінійного програмування Оптимальні значення ймовірностей xi, i = 1, 2, ...,
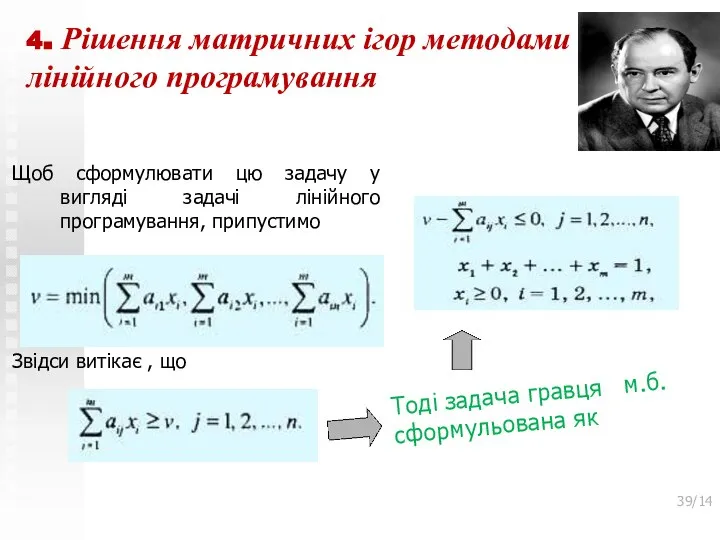
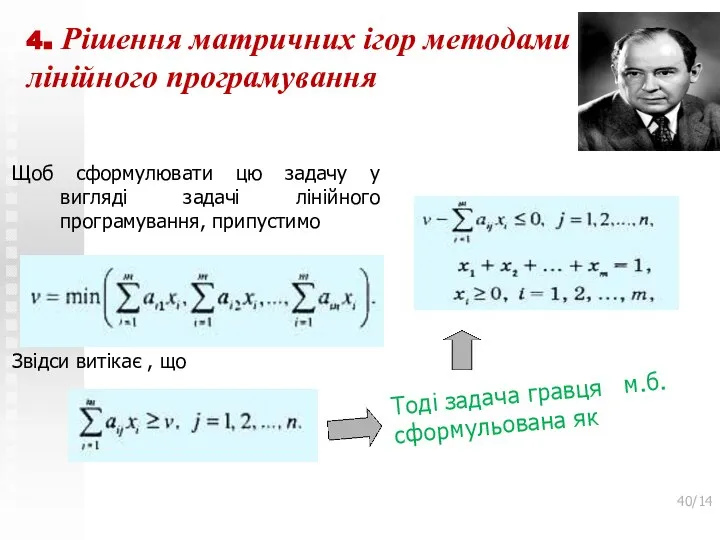
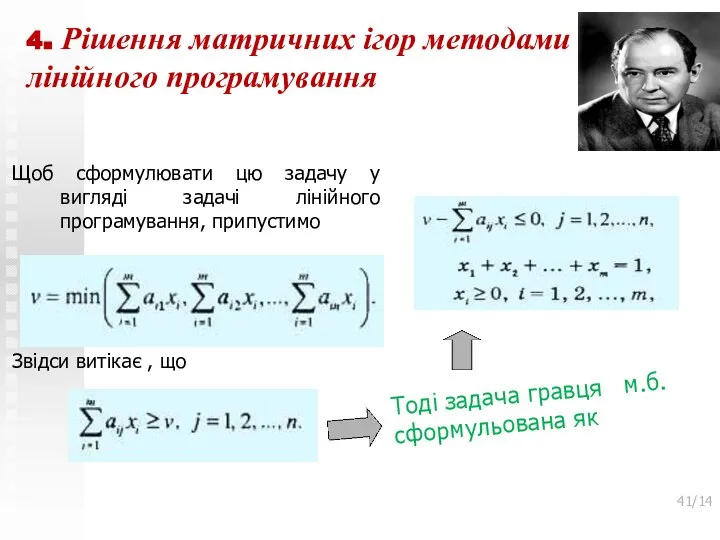
- 39. 4. Рішення матричних ігор методами лінійного програмування Щоб сформулювати цю задачу у вигляді задачі лінійного програмування,
- 40. 4. Рішення матричних ігор методами лінійного програмування Щоб сформулювати цю задачу у вигляді задачі лінійного програмування,
- 41. 4. Рішення матричних ігор методами лінійного програмування Щоб сформулювати цю задачу у вигляді задачі лінійного програмування,
- 42. 4. Рішення матричних ігор методами лінійного програмування Відзначимо, що ціна гри v може бути як позитивною,
- 43. 4. Рішення матричних ігор методами лінійного програмування Дві отримані задачі оптимізують одну і ту ж (не
- 44. 5. Приклад рішення матричної гри методами лінійного програмування Теорія Прийняття рішень © ЄА. Лавров, 2014-2019 /100
- 45. 5. Приклад рішення матричної гри методами лінійного програмування Задача Значення ціни гри v знаходиться між -2
- 46. 5. Приклад рішення матричної гри методами лінійного програмування Задача Задача лінійного програмування и для гравця А
- 47. 5. Приклад рішення матричної гри методами лінійного програмування Задача Задача лінійного програмування и для гравця В
- 48. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006 /20
- 50. Скачать презентацию







































 Forming of political world map
Forming of political world map Последние реализованные задачи и планы ЮТС по проектам
Последние реализованные задачи и планы ЮТС по проектам Положительные стороны занятий в секции спортивного ориентирования
Положительные стороны занятий в секции спортивного ориентирования Методическая разработка «Адаптивная физическая культура»
Методическая разработка «Адаптивная физическая культура» Расчет на прочность. (Лекция 6)
Расчет на прочность. (Лекция 6) Модуль1.
Модуль1.  ОРГАНІЗАЦІЯ ВИРОБНИЦТВА
ОРГАНІЗАЦІЯ ВИРОБНИЦТВА Архитектура Web-баз данных. Лекция 3.19
Архитектура Web-баз данных. Лекция 3.19 Лидеры и элиты в политической жизни
Лидеры и элиты в политической жизни Пересечение поверхности плоскостью
Пересечение поверхности плоскостью Этап «выявление потребностей»
Этап «выявление потребностей» Лисичка-сестричка и серый волк - презентация для начальной школы
Лисичка-сестричка и серый волк - презентация для начальной школы КПД двигателей внутреннего сгорания
КПД двигателей внутреннего сгорания Как корабль назовёшь, так он и полетит
Как корабль назовёшь, так он и полетит Библейская теология работы и устойчивости
Библейская теология работы и устойчивости Проективный метод в психодиагностике
Проективный метод в психодиагностике Банковское дело
Банковское дело Корейский буддизм в колониальный период
Корейский буддизм в колониальный период Карловы Вары
Карловы Вары Поверхности
Поверхности  УВВ
УВВ Новый год и Рождество
Новый год и Рождество Выполнили Галибина Л. и Кошарный И. Т-114
Выполнили Галибина Л. и Кошарный И. Т-114  Effects of sanctions on Russia & the European Union
Effects of sanctions on Russia & the European Union Средства создания презентаций MS PowerPoint
Средства создания презентаций MS PowerPoint МОУ средняя общеобразовательная школа №9 г. Искитима Новосибирской области Научно-исследовательская работа по теме «В школу с у
МОУ средняя общеобразовательная школа №9 г. Искитима Новосибирской области Научно-исследовательская работа по теме «В школу с у Теракт в метро Санкт- Петербург
Теракт в метро Санкт- Петербург Микропроцессорная техника
Микропроцессорная техника