Содержание
- 2. 1. Системы координат и векторы. - Как найти расстояние между двумя точками? и Что такое вектор?
- 3. Какие вектора называются линейно независимыми? Линейно зависимыми? - Что является скалярным произведением двух векторов? - Что
- 4. 2. Уравнения прямой и плоскости. Уравнение прямой на плоскости в декартовой системе координат можно задать уравнением
- 5. Координаты точки, соответствующей некоторому значению этого параметра, определяются соотношениями: Прямая в пространстве задается аналогично: Через каждую
- 6. Плоскость в пространстве можно задать, указав вектор нормали к ней и какую-либо точку, принадлежащую данной плоскости.
- 7. Если каноническое уравнение плоскости умножить на какой-либо отличный от нуля множитель, то оно будет описывать ту
- 8. В каких плоскостях лежат эти вектора? Каноническое уравнение плоскости будет иметь вид: Определим значение . Так
- 9. Окончательно каноническое уравнение плоскости будет иметь вид:
- 10. 3. Аналитическое представление кривых и поверхностей. Кривая на плоскости - это геометрическое место точек удовлетворяющих уравнению
- 13. Задает ли следующее уравнение поверхность в пространстве?
- 15. 4. Пересечение луча с плоскостью и сферой.
- 16. В каком случае может существовать такая точка?
- 19. 5. Интерполяция функций одной и двух переменных. Если функция задается своими значениями на некотором дискретном множестве
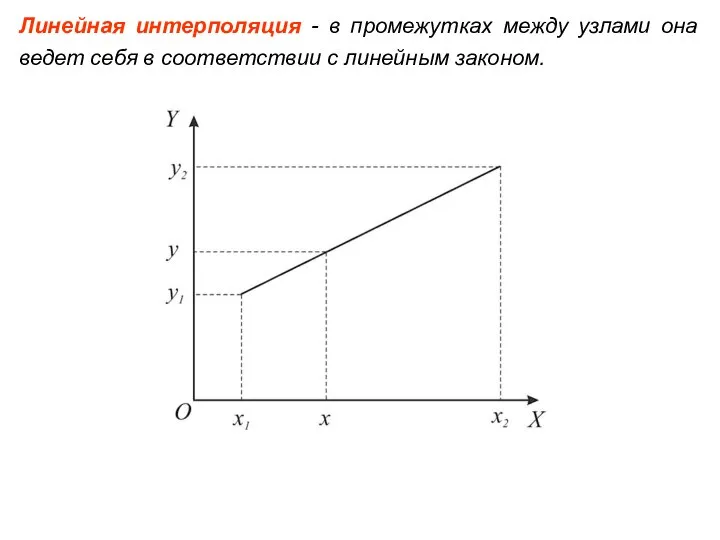
- 20. Линейная интерполяция - в промежутках между узлами она ведет себя в соответствии с линейным законом.
- 21. Рассмотрим задачу интерполяции функций двух переменных (по трем заданным точкам с помощью кусочно-линейной функции).
- 23. Эти числа неотрицательны и удовлетворяют следующим соотношениям:
- 24. Эти соотношения будем рассматривать как уравнения для нахождения чисел Определитель этой системы уравнений:
- 27. Скачать презентацию























 Развитие на стартиращи иновативни предприятия чрез подкрепа за внедряване на иновативни продукти, процеси и услуги април 2010
Развитие на стартиращи иновативни предприятия чрез подкрепа за внедряване на иновативни продукти, процеси и услуги април 2010 Вентиляция и кондиционирование воздуха. Лекция 3
Вентиляция и кондиционирование воздуха. Лекция 3 Минувшее в настоящем. Ценить прошлое и настоящее
Минувшее в настоящем. Ценить прошлое и настоящее Статистика расходов и потребления
Статистика расходов и потребления . Склеродермия
. Склеродермия ЛИЧНОСТЬ КАК ПРЕДМЕТ ВОСПИТАНИЯ, ВНЕШНИЕ И ВНУТРЕННИЕ ФАКТОРЫ ЕЕ РАЗВИТИЯ
ЛИЧНОСТЬ КАК ПРЕДМЕТ ВОСПИТАНИЯ, ВНЕШНИЕ И ВНУТРЕННИЕ ФАКТОРЫ ЕЕ РАЗВИТИЯ Одномерные массивы. Сортировка пузырьком
Одномерные массивы. Сортировка пузырьком Классификация на основе оценки апостериорной вероятности
Классификация на основе оценки апостериорной вероятности  Право. Административное право. Задания для выполнения
Право. Административное право. Задания для выполнения Основы проектирования и оборудование
Основы проектирования и оборудование 骑车旅行记
骑车旅行记 О комнатных растениях - презентация для начальной школы
О комнатных растениях - презентация для начальной школы СМИ и коммуникация
СМИ и коммуникация Средняя величина и её свойство
Средняя величина и её свойство Правила цифрового описания объектов
Правила цифрового описания объектов  Теория подражания. Идеи Габриедя Тарда Выполнила студентка группы Ю-104 Чуева Яна
Теория подражания. Идеи Габриедя Тарда Выполнила студентка группы Ю-104 Чуева Яна Значение слова пассия
Значение слова пассия Семейное право
Семейное право Обогащение на шлюзах и сепараторах. Принцип работы
Обогащение на шлюзах и сепараторах. Принцип работы Балет - Презентация_
Балет - Презентация_ Схемотехника комбинационных узлов
Схемотехника комбинационных узлов Викторина по творчеству и биографии Антона Павловича Чехова - презентация для начальной школы_
Викторина по творчеству и биографии Антона Павловича Чехова - презентация для начальной школы_ Роль двигательной активности в формировании здоровья человека. Оздоровительная физическая культура
Роль двигательной активности в формировании здоровья человека. Оздоровительная физическая культура Процесс демократизации в мире
Процесс демократизации в мире Контрактная служба в армии
Контрактная служба в армии Круговая эстафета с предметами. Урок физической культуры 5 класс
Круговая эстафета с предметами. Урок физической культуры 5 класс Биоценология
Биоценология Эрнест Резерфорд
Эрнест Резерфорд