Содержание
- 2. 09/02/2023 Теоретические основы проекционных методов Основная задача классического вариационного исчисления: Найти такую u=u(x) a≤x≤b u(a)=u0 u(b)=u1
- 3. 09/02/2023 Например u(x) – путь пройденный автомобилем за время 0≤x≤T - скорость Затраты пропорциональны квадрату скорости
- 4. 09/02/2023 Сведение решения ДУ к минимизации функционала Таким образом задача нахождения минимума функционала сводится к решению
- 5. 09/02/2023 Функционал, минимум которого достигается на решении ДУ, имеет вид Самым универсальным и во многих случаях
- 6. 09/02/2023 Метод Ритца Выбираем базис Свойства линейной независимости и полноты Ищем решение в виде Подставляем в
- 7. 09/02/2023 Примеры базисных функций обладающих полнотой Полиномы Тригонометрические функции От удачного выбора базиса зависит эффективность решения
- 8. 09/02/2023 Минимизация квадратичного функционала с линейным оператором L После подстановки uN(x) Воспользуемся условием экстремума Получаем СЛАУ
- 9. 09/02/2023 Системы проекционных уравнений Запишем Или Проекция Можно заметить, что эта система получается из исходной краевой
- 10. 09/02/2023 Проекционные методы Впервые идею такого решения ДУ (не обращаясь к вариационной задаче) предложил в 1915
- 11. 09/02/2023 Решение одномерной краевой задачи Найти решение Ищем решение в виде Проекционное уравнение преобразуем
- 12. 09/02/2023 Решение одномерной краевой задачи (продолжение1) Подставляем uN Преобразуем и получаем систему основных проекционных уравнений В
- 13. 09/02/2023 Задача Дирихле Выбираем систему базисных функций вида: В силу того, что Получаем проекционное уравнение вида
- 14. 09/02/2023 Программная реализация задачи Дирихле function V2_1; Be0=1; be1=0; N=4; M=10; for i=1:N F1 = @(x)f(x).*sin(i*pi*x)-g(x).*(be1-be0).i*pi*cos(i*pi*x);
- 15. 09/02/2023 Задача со свободным левым концом Выбираем базис вида Первый член проекционного уравнения используя гр. условие:
- 16. 09/02/2023 Задача со свободным левым концом (продолжение) Проекционное ур-е После подстановки функций базиса:
- 17. 09/02/2023 Программная реализация задачи со свободным левым концом function V2_2(al0,be0,be1,N,M); for i=1:N F1 = @(x)f(x).*sin(0.5*i*pi*(1-x))- g(x).*be1.*0.5*i*pi*cos(0.5*i*pi*(1-x));
- 18. 09/02/2023 Задача со свободным правым концом Выбираем базис вида Первый член проекционного ур-я Проекционное уравнение
- 19. 09/02/2023 Задача со свободным правым концом (продолжение) Проекционное уравнение После подстановки функций базиса
- 20. 09/02/2023 Программная реализация задачи со свободным правым концом function V2_3(al1,be0,be1,N,M); for i=1:N F1 = @(x)f(x).*sin(0.5*i*pi*x)- g(x).*be0.*0.5*i*pi*cos(0.5*i*pi*x);
- 21. 09/02/2023 Двумерная краевая задача Дирихле Выбираем базис Решение ищем в виде Проекционное уравнение
- 22. 09/02/2023 Двумерная краевая задача Дирихле (продолжение) Воспользуемся методом интегрирования по частям для двумерного случая Получаем проекционное
- 23. 09/02/2023 Сведение трехмерной задачи для ДУ в частных производных к решению задачи для системы ОДУ методом
- 24. 09/02/2023 Метод Канторовича (продолжение)
- 26. Скачать презентацию























 Здравоохранение1
Здравоохранение1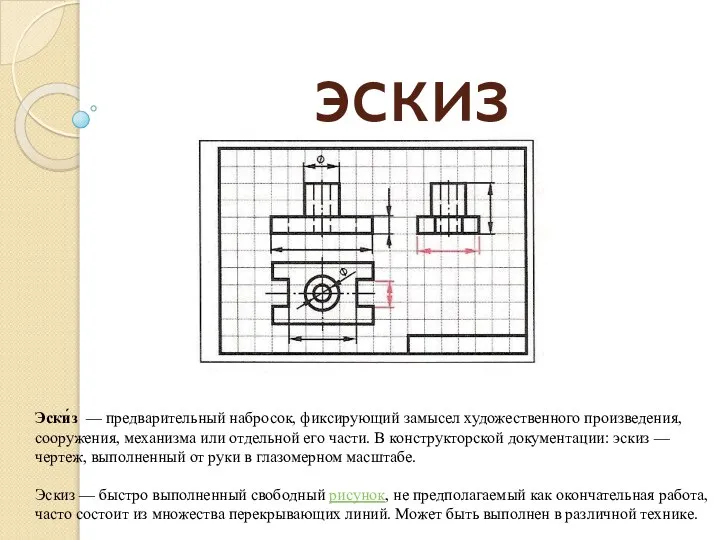 Эскиз. Алгоритм выполнения эскиза
Эскиз. Алгоритм выполнения эскиза Честь
Честь Центрифуга
Центрифуга СРС ТЕМА: Повреждение черепа и головного мозга Подготовил: Кульдеев С. К. Группа 306 «А» ОМ Проверила: Иминова С. А.
СРС ТЕМА: Повреждение черепа и головного мозга Подготовил: Кульдеев С. К. Группа 306 «А» ОМ Проверила: Иминова С. А. metody_issledovaniya_v_biologii
metody_issledovaniya_v_biologii НАЧАЛЬНАЯ ШКОЛА РЕАЛИЗАЦИЯ ПРИНЦИПА ПСИХОЛОГИЧЕСКОЙ КОМФОРТНОСТИ В ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ НАЧАЛЬНЫХ КЛАССОВ ШКОЛЫ №1245
НАЧАЛЬНАЯ ШКОЛА РЕАЛИЗАЦИЯ ПРИНЦИПА ПСИХОЛОГИЧЕСКОЙ КОМФОРТНОСТИ В ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ НАЧАЛЬНЫХ КЛАССОВ ШКОЛЫ №1245 Глава 5. Экономика мира 33. Обменные курсы валют
Глава 5. Экономика мира 33. Обменные курсы валют LuxCare. Самоомоложение. Косметика премиум-класса элитная косметика для роскошного ухода за кожей лица
LuxCare. Самоомоложение. Косметика премиум-класса элитная косметика для роскошного ухода за кожей лица Особенности юридической техники: Мальта, Кипр, Гибралтар
Особенности юридической техники: Мальта, Кипр, Гибралтар Система маркетинговых стратегий предприятия: Портфельные стратегии( матрица БКГ, матрица Джи-И-Маккензи), стратегии роста(матрица
Система маркетинговых стратегий предприятия: Портфельные стратегии( матрица БКГ, матрица Джи-И-Маккензи), стратегии роста(матрица  Презентация "Эконометрика" - скачать презентации по Экономике__
Презентация "Эконометрика" - скачать презентации по Экономике__ Храм во имя святой Татианы мученицы
Храм во имя святой Татианы мученицы Безлифтовые жилые дома с общеквартирными коммуникациями
Безлифтовые жилые дома с общеквартирными коммуникациями Культура скифов
Культура скифов Понятие власти
Понятие власти Слабые связи
Слабые связи  США: империализм и вступление в мировую политику
США: империализм и вступление в мировую политику Доказательный подход к управлению социальными проектами
Доказательный подход к управлению социальными проектами Украшения в древней руси Женские Дмитрий Голышев 6 б класс 2009 г.
Украшения в древней руси Женские Дмитрий Голышев 6 б класс 2009 г. Лекція 13. Хеш таблиці
Лекція 13. Хеш таблиці Программирование на алгоритмическом языке. Часть III (9 класс)
Программирование на алгоритмическом языке. Часть III (9 класс) Детская квадрошкола "ATV Kids Academy"
Детская квадрошкола "ATV Kids Academy" Косметический ремонт и шумоизоляция актового зала
Косметический ремонт и шумоизоляция актового зала Выколотка. Чеканка. Гравировка.
Выколотка. Чеканка. Гравировка. Презентация Инкассовая форма расчета
Презентация Инкассовая форма расчета Расчет строп и траверс. Расчет якорных закреплений плавучих средств
Расчет строп и траверс. Расчет якорных закреплений плавучих средств «Годовой отчет: дань моде, требование законодательства или бизнес-потребность?» Борис Аксёнов Бухгалтерская служба ОАО «РЖ
«Годовой отчет: дань моде, требование законодательства или бизнес-потребность?» Борис Аксёнов Бухгалтерская служба ОАО «РЖ