Случайные распределения Метод обратной функции. Метод фон Неймана. Распределение Пуассона. Нормальное распределение.
Содержание
- 2. Вероятность в физике Понятие вероятности является одним из ключевых в квантовой физике Современное описание квантовых систем
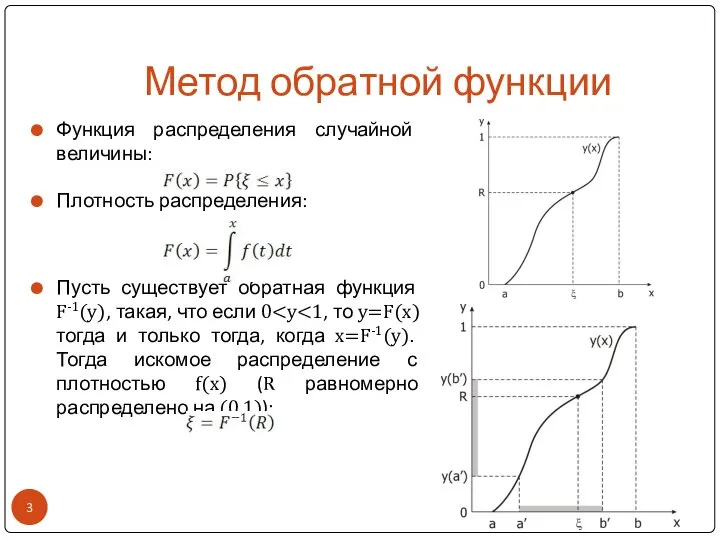
- 3. Метод обратной функции Функция распределения случайной величины: Плотность распределения: Пусть существует обратная функция F-1(y), такая, что
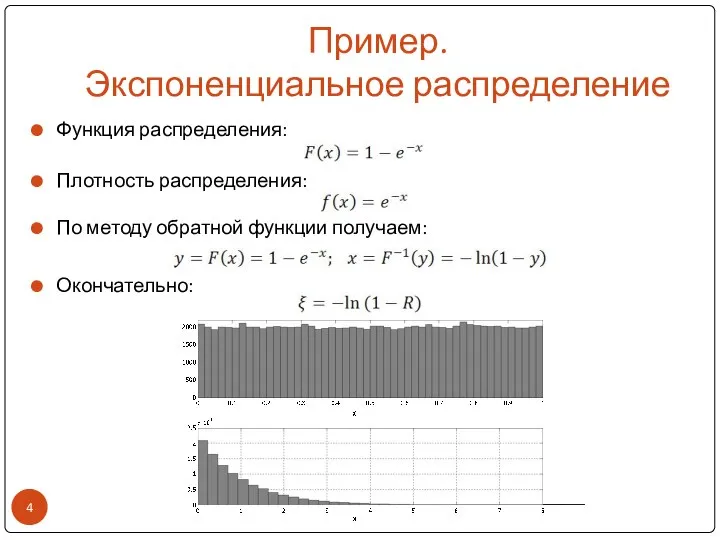
- 4. Пример. Экспоненциальное распределение Функция распределения: Плотность распределения: По методу обратной функции получаем: Окончательно:
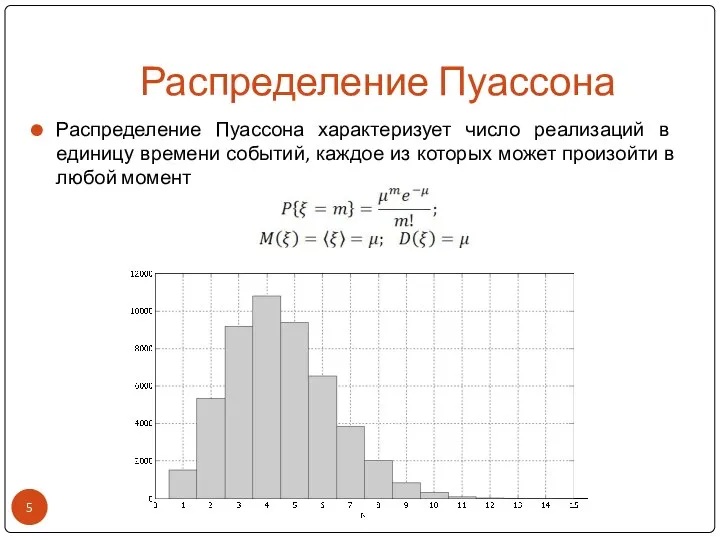
- 5. Распределение Пуассона Распределение Пуассона характеризует число реализаций в единицу времени событий, каждое из которых может произойти
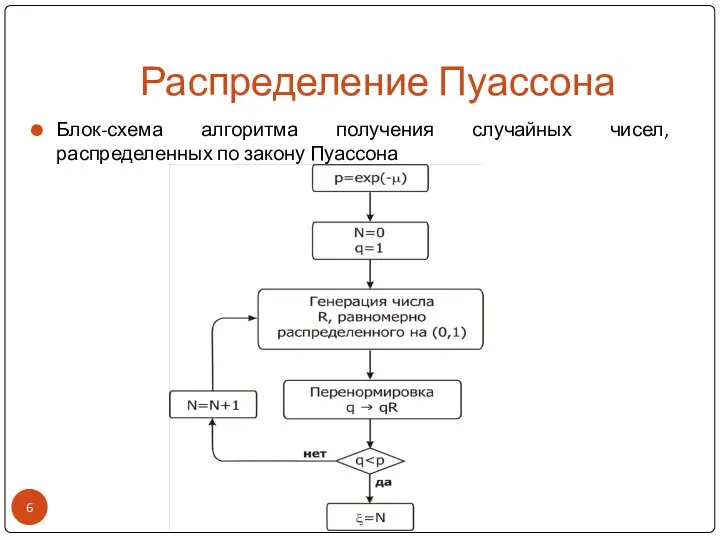
- 6. Распределение Пуассона Блок-схема алгоритма получения случайных чисел, распределенных по закону Пуассона
- 7. Метод фон Неймана Случайная величина ξ определена на интервале (a,b), и ее плотность распределения ограничена: Генерируются
- 8. Нормальное распределение Нормальный закон распределения случайных величин, часто также называемый законом Гаусса, играет исключительно важную роль
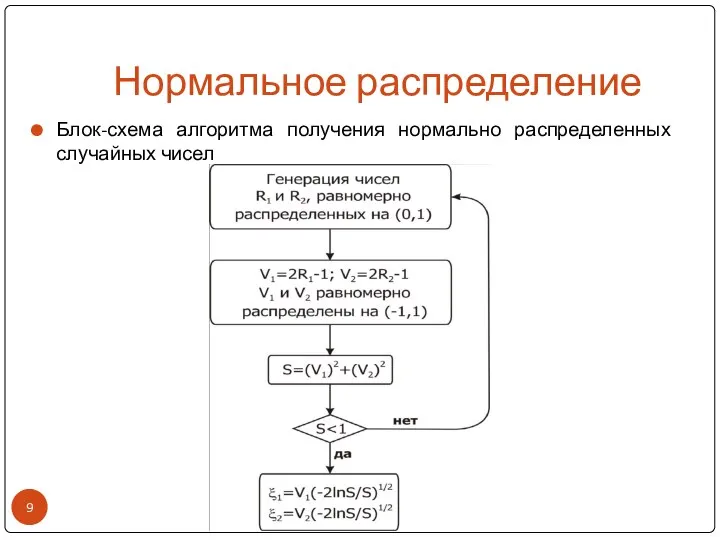
- 9. Нормальное распределение Блок-схема алгоритма получения нормально распределенных случайных чисел
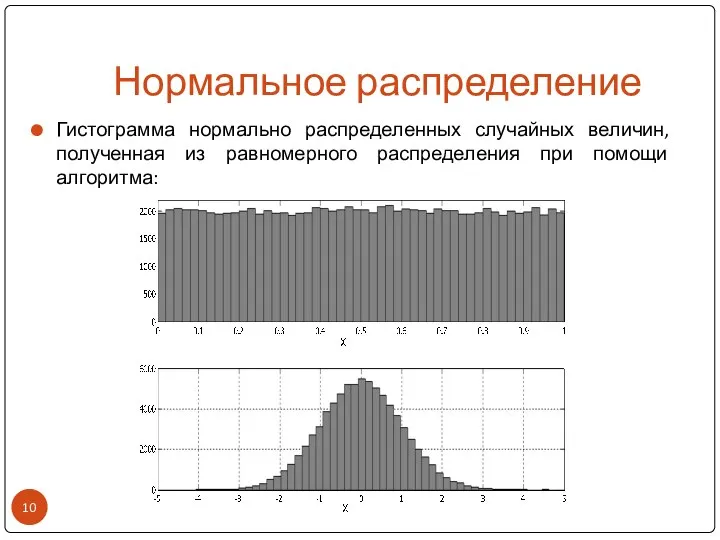
- 10. Нормальное распределение Гистограмма нормально распределенных случайных величин, полученная из равномерного распределения при помощи алгоритма:
- 11. Почти линейное распределение Плотность распределения: Почти линейному распределению удовлетворяет целый класс функций
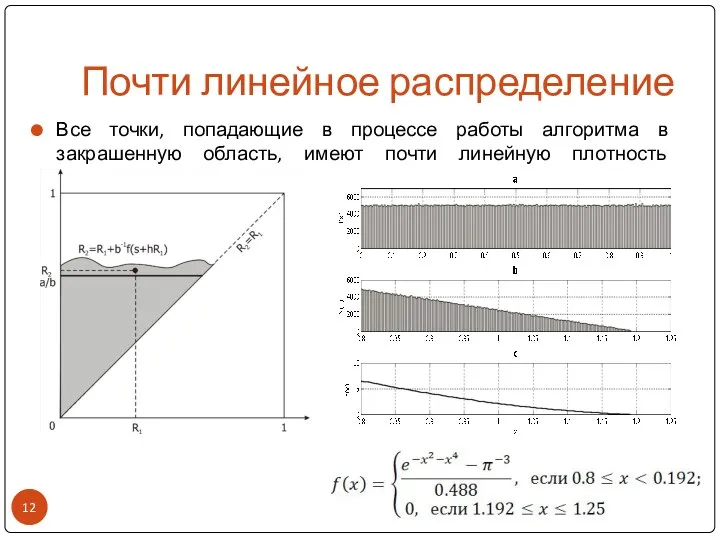
- 12. Почти линейное распределение Все точки, попадающие в процессе работы алгоритма в закрашенную область, имеют почти линейную
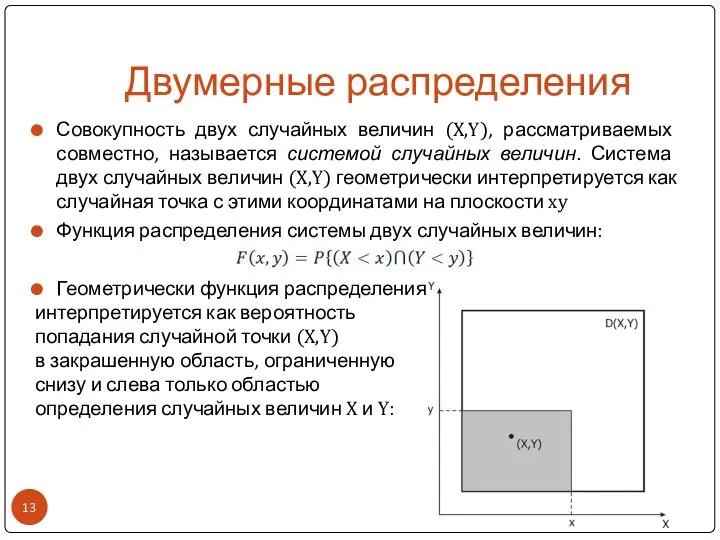
- 13. Двумерные распределения Совокупность двух случайных величин (X,Y), рассматриваемых совместно, называется системой случайных величин. Система двух случайных
- 14. Двумерные распределения Плотность распределения системы двух случайных величин: Функция распределения системы случайных величин: Пример Сначала генерируем
- 15. Двумерные распределения Закон распределения случайной величины x при заданном z: Случайная величина x распределена равномерно на
- 17. Скачать презентацию






 САВЕЗ САМОСТАЛНИХ СИНДИКАТА ГРАДА НОВОГ САДА И ОПШТИНА. - презентация
САВЕЗ САМОСТАЛНИХ СИНДИКАТА ГРАДА НОВОГ САДА И ОПШТИНА. - презентация Индексы
Индексы Социальная поддержка семей, имеющих детей
Социальная поддержка семей, имеющих детей  Презентация Разрешительный порядок вывоза культурных ценностей из Российской Федерации
Презентация Разрешительный порядок вывоза культурных ценностей из Российской Федерации Весна
Весна Сборка компьютера
Сборка компьютера Взаимосвязь функций управления
Взаимосвязь функций управления Структура и содержание физической подготовки девушек – спринтеров 18-19 лет в годичном цикле тренировки
Структура и содержание физической подготовки девушек – спринтеров 18-19 лет в годичном цикле тренировки profit and loss account
profit and loss account Жилой комплекс «Васильевский квартал»
Жилой комплекс «Васильевский квартал» Факторы развития одаренности Корчуганова Ирина Павловна, доцент, кандидат психологических наук 26.04.2011
Факторы развития одаренности Корчуганова Ирина Павловна, доцент, кандидат психологических наук 26.04.2011 Анатомия человека
Анатомия человека Centrum logistyczne
Centrum logistyczne Презентация на тему "Совместная деятельность с детьми средней группы по формированию правил дорожного движения и поведения на
Презентация на тему "Совместная деятельность с детьми средней группы по формированию правил дорожного движения и поведения на  Окружающий мир 3класс Тема «Разнообразие растений» Учитель начальных классов Шеремет Н.Д. МБОУ «СОШ № 37» г. Симферополь Респ
Окружающий мир 3класс Тема «Разнообразие растений» Учитель начальных классов Шеремет Н.Д. МБОУ «СОШ № 37» г. Симферополь Респ Освоение космоса
Освоение космоса Биохимические закономерности адаптации к мышечной работе
Биохимические закономерности адаптации к мышечной работе Вяжущие вещества. Виды
Вяжущие вещества. Виды Самый вкусный и ароматный бизнес
Самый вкусный и ароматный бизнес Контроль со стороны профсоюзов за соблюдением законодательства по охране труда в организациях Свердловской области
Контроль со стороны профсоюзов за соблюдением законодательства по охране труда в организациях Свердловской области Международное сотр в УС
Международное сотр в УС Подготовка к ЕГЭ 2014 по математике Решение задания С1
Подготовка к ЕГЭ 2014 по математике Решение задания С1 Давид Самойлов Белые стихи
Давид Самойлов Белые стихи Интегрированный банк данных «ИБД-Регион»
Интегрированный банк данных «ИБД-Регион» Будова української хати
Будова української хати Массивы (Turbo Pascal)
Массивы (Turbo Pascal) Маркетинговые исследования
Маркетинговые исследования Презентация Анализ экономического потенциала Восточной зоны РФ
Презентация Анализ экономического потенциала Восточной зоны РФ