Виды работ при построении триангуляции

Последовательность видов работ при построении триангуляции.
Приведение измеренных направлений к

1. Последовательность видов работ при построении триангуляции.
При создании геодезических сетей

4.Определение значений длин и дирекционных углов выходных сторон.
5. Измерение углов треугольников.
6.Обработка

Во время рекогносцировки при необхо-димости вносят изменения в проект.
Длины выходных сторон

2. Приведение измеренных направлений к центрам пунктов.
Геодезический знак стремятся строить так,

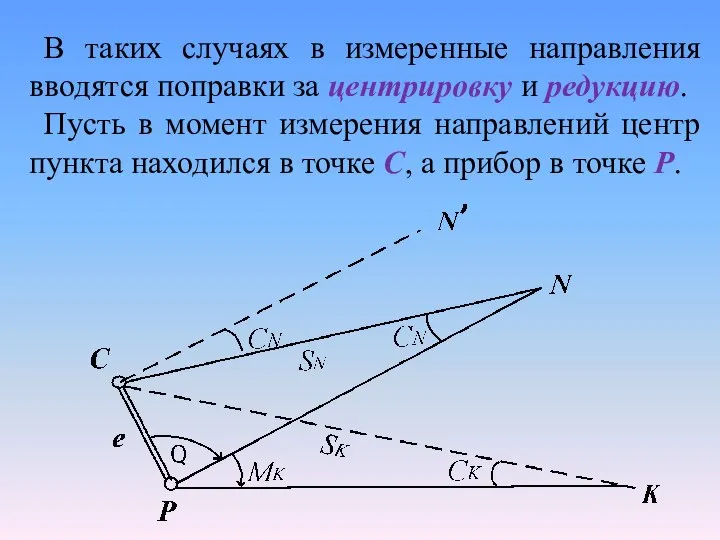
В таких случаях в измеренные направления вводятся поправки за центрировку и

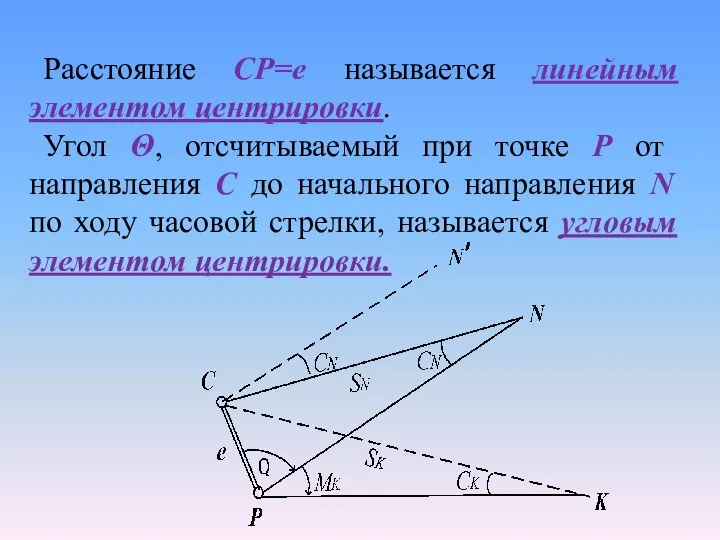
Расстояние CP=е называется линейным элементом центрировки.
Угол Θ, отсчитываемый при точке

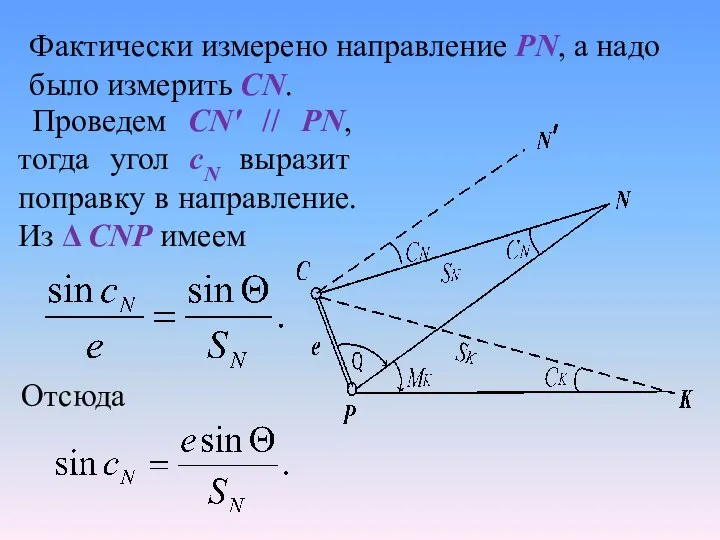
Проведем СN' // PN, тогда угол сN выразит поправку в направление.

По малости угла сN можно записать

Аналогично можно найти поправку в любое

В общем виде без индексов формулу для вычисления поправок за центрировку

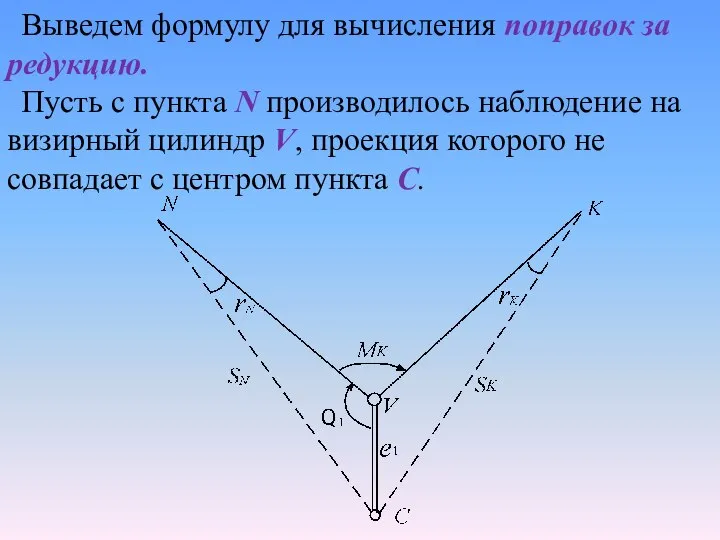
Выведем формулу для вычисления поправок за редукцию.
Пусть с пункта N

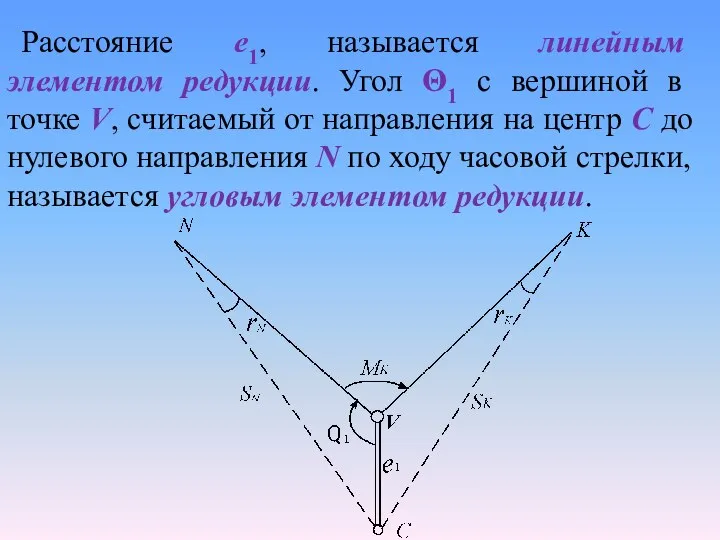
Расстояние e1, называется линейным элементом редукции. Угол Θ1 с вершиной в

Из рис. видно, что в направление NV нужно
ввести поправку

а в

В общем виде формулу для вычисления поправок за редукцию можно записать

3. Способы определения элементов приведения.
Величины e, e1, Θ, Θ1 необходимые для

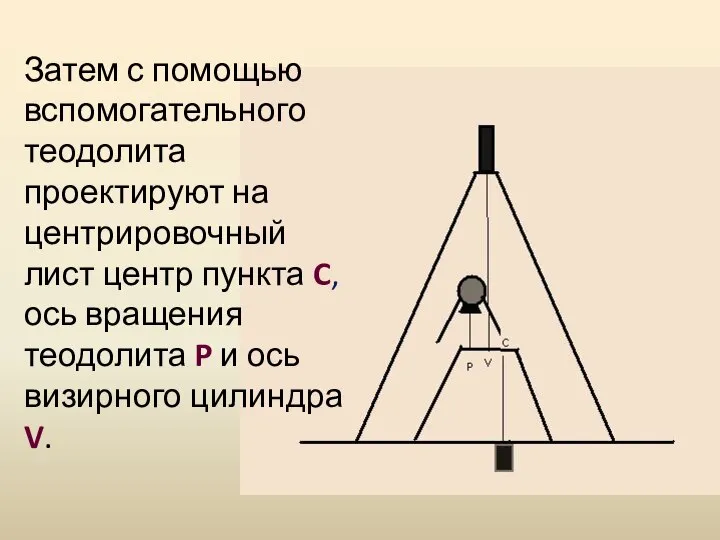
Затем с помощью вспомогательного теодолита проектируют на центрировочный лист центр пункта

Проектирование выполняют при двух положениях круга с трех точек, расположенных так,

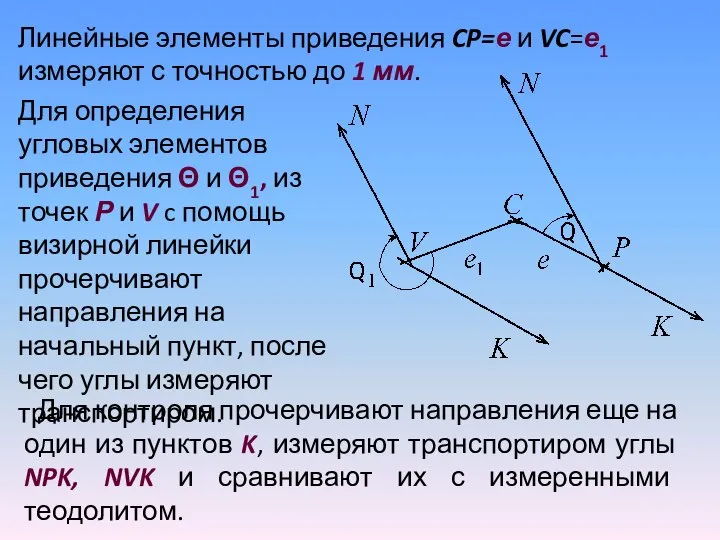
Для определения угловых элементов приведения Θ и Θ1, из точек Р

Графический способ применяют в случаях, когда е и е1 небольшие.
Если

4. Предварительная обработка триангуляция.
После выполнения полевых работ приступают к предварительной обработке

4. Выполняют предварительное решение треугольников.
5. Вычисляют поправки за центрировку и

8. Вычисляют угловые невязки и проверяет их допустимость.
9. Делают оценку

5. Виды условных уравнений в триангуляции.
При построении триангуляции в целях

Если сеть содержит избыточные исходные данные, то она несвободная. Каждое избыточное

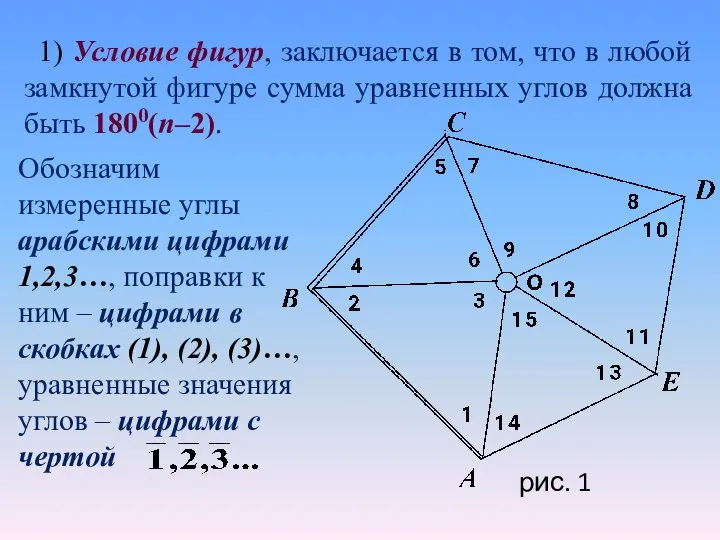
1) Условие фигур, заключается в том, что в любой замкнутой фигуре

Тогда условие фигуры ABO запишется так

(1)

Учитывая, что

получим
1+(1)+2+(2)+3+(3)–1800

Обозначим
1+2+3–1800 = w. (2)
Тогда
(1)+(2)+(3)+w = 0. (3)
Полученное уравнение называется

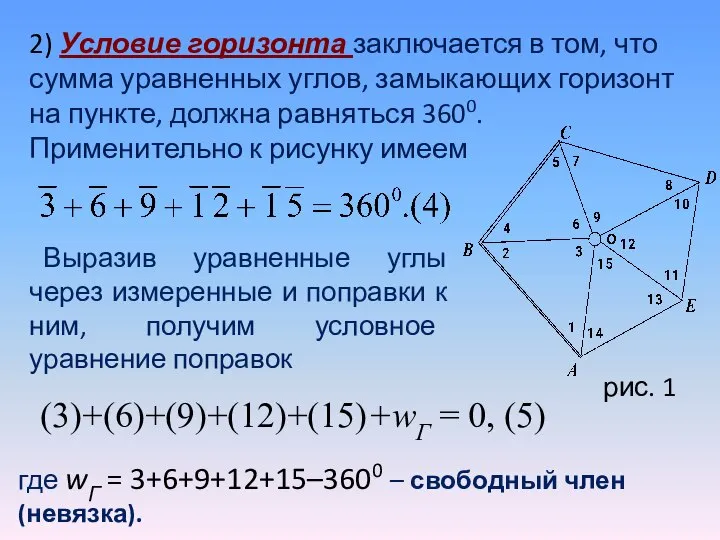
2) Условие горизонта заключается в том, что сумма уравненных углов, замыкающих

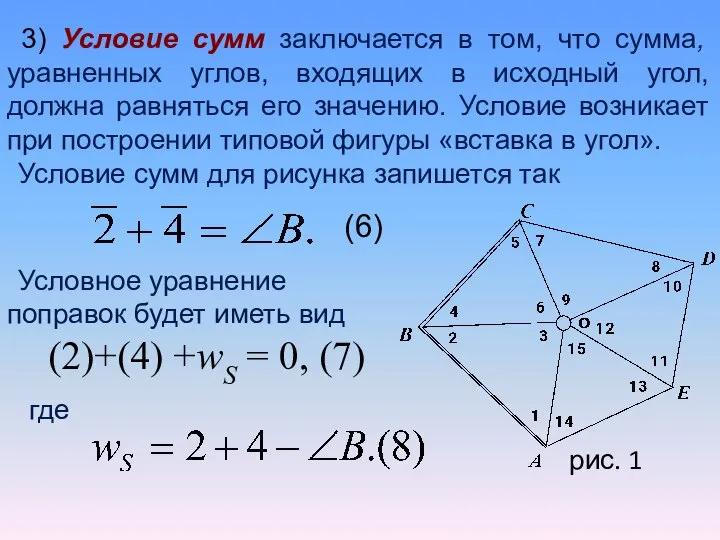
3) Условие сумм заключается в том, что сумма, уравненных углов, входящих

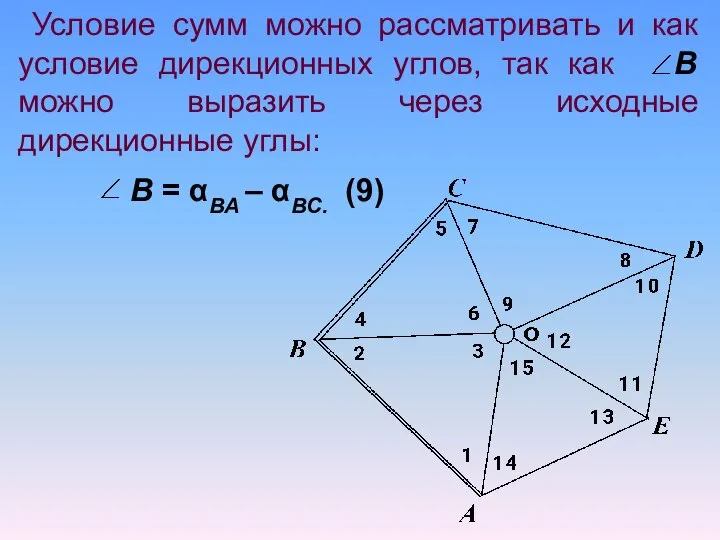
4) Полюсное условие заключается в том, что длина одной и той

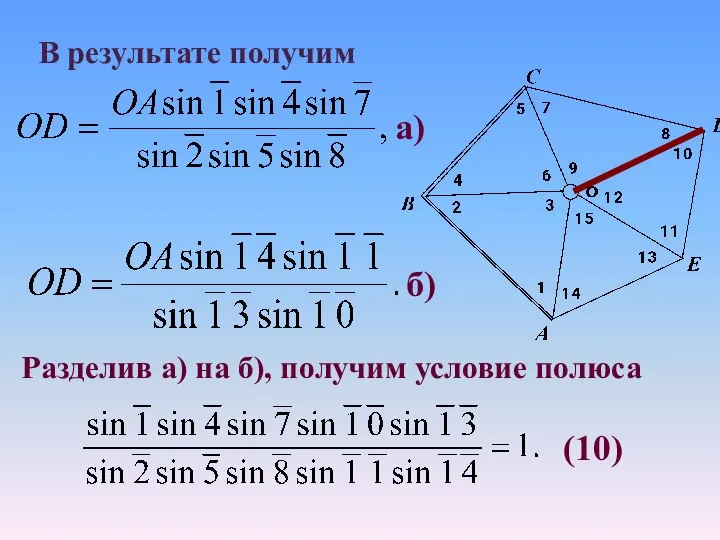
В результате получим

а)

б)

Разделив а) на б), получим условие полюса

Равенство (10) можно получить, решая треугольники по ходу часовой стрелки, начиная

В результате получим

Если второе слагаемое умножить и разделить на sin1, то его с

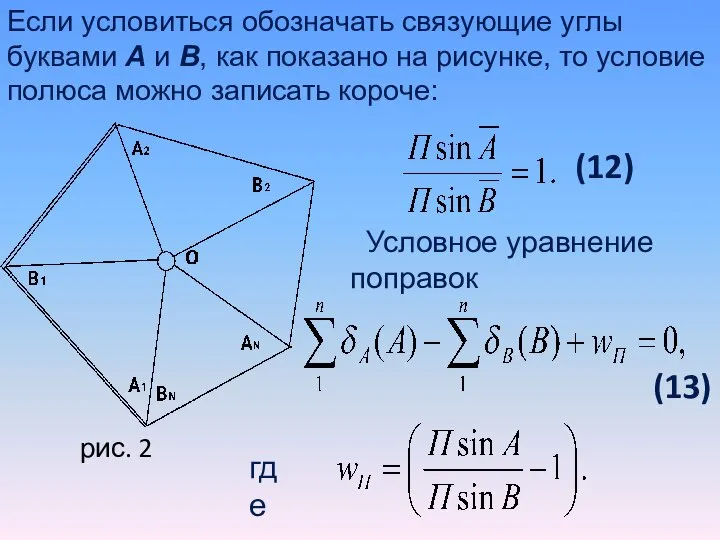
Тогда полюсное условное уравнение поправок в угловой мере будет иметь вид

Если условиться обозначать связующие углы буквами А и В, как показано

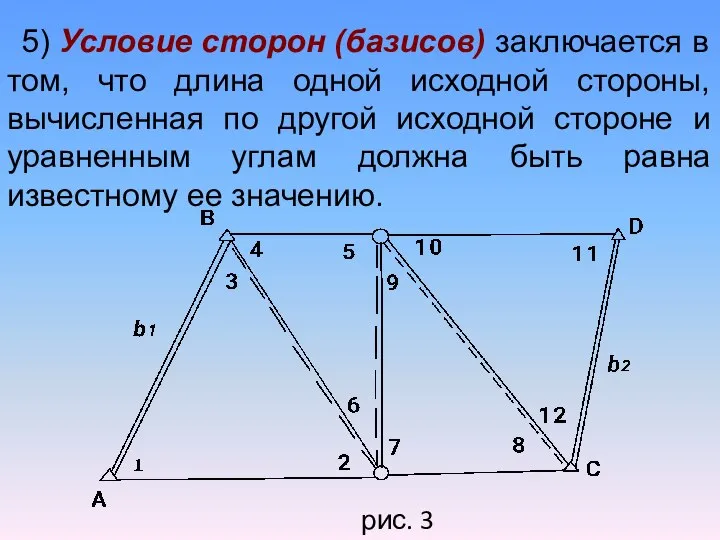
5) Условие сторон (базисов) заключается в том, что длина одной исходной

Для данной цепи треугольников, заключенной между исходными сторонами b1 и b2

Это равенство и будет выражать условие сторон. Оно аналогично (10). Для

где

(16)

Если связующие углы числителя обозначить через А, а в знаменателе через

(18)

(19)

6) Условие дирекционных углов заключается в том, что дирекционный угол одной

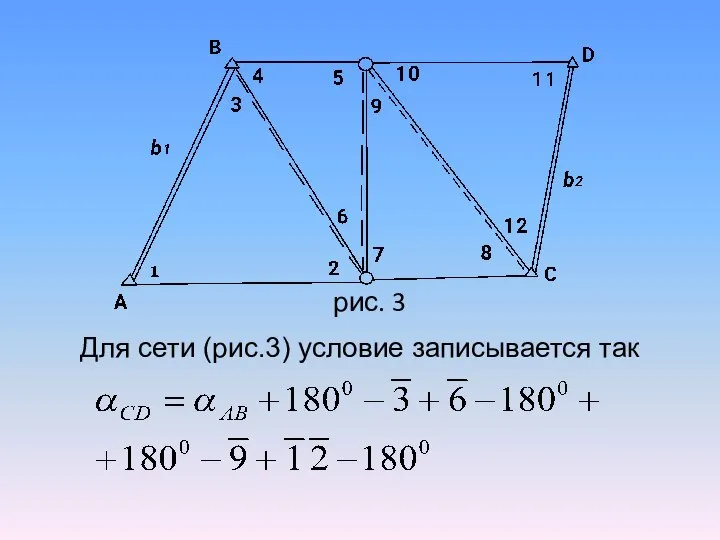
Для сети (рис.3) условие записывается так

рис. 3