Содержание
- 2. Ошибки и их виды Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение
- 3. Изучением основных свойств и закономерностей действия погрешностей измерений, разработкой методов получения наиболее точного значения измеряемой величины
- 4. Каждый из перечисленных факторов порождает целый ряд элементарных ошибок. Суммарное действие элементарных ошибок образует ошибку результата
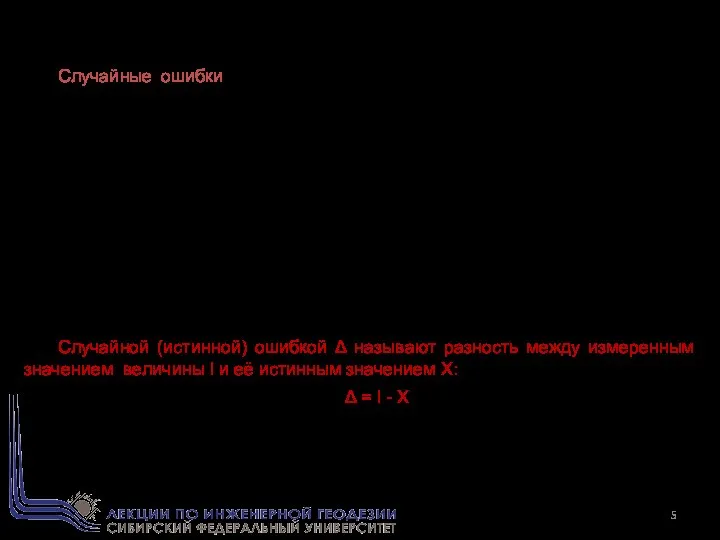
- 5. Случайные ошибки – это ошибки, размер и влияние которых на каждый отдельный результат измерения остается неизвестным.
- 6. Свойства случайных ошибок 1. При определенных условиях измерений случайные ошибки по абсолютной величине не могут превышать
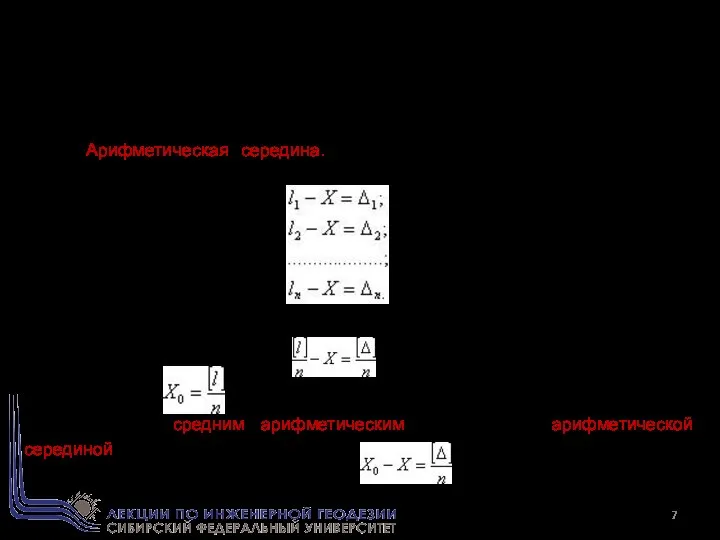
- 7. Последнее свойство случайных ошибок позволяет установить принцип получения из ряда измерений одной и той же величины
- 8. (1) где n — число измерений данной величины. по четвертому свойству ошибок можно написать: что означает,
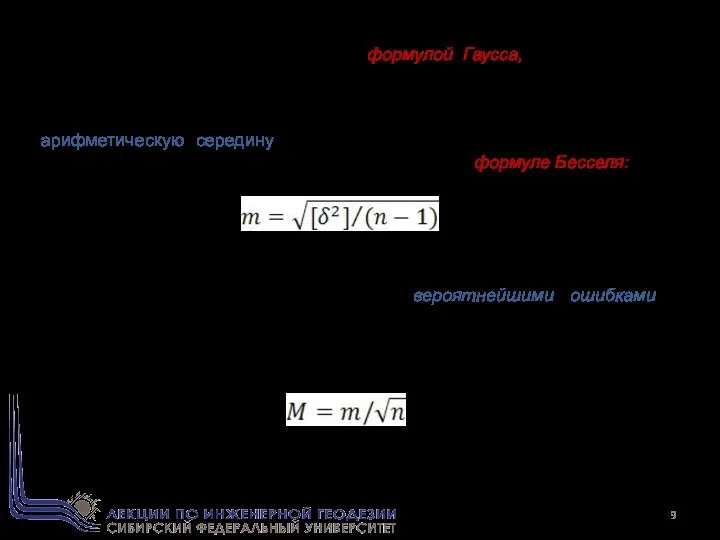
- 9. Формула (1), которую называют формулой Гаусса, применима для случаев, когда известно истинное значение измеряемой величины Х.
- 10. Предельная ошибка В соответствии с первым свойством случайных ошибок для абсолютной величины случайной погрешности при данных
- 11. Двойные измерения Часто в практике для контроля и повышения точности определяемую величину измеряют дважды — в
- 12. Относительная ошибка В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней
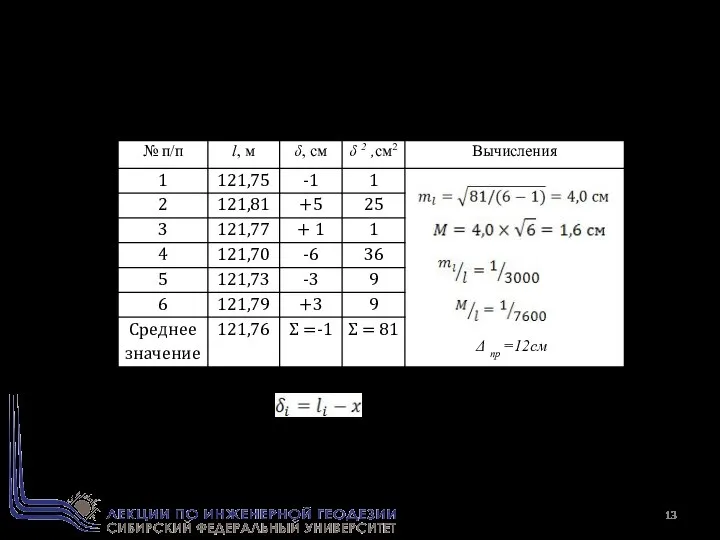
- 13. Пример. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность
- 14. Вычислительная обработка результатов геодезических измерений Для производства топографической съемки создается геодезическое съемочное обоснование в виде закрепленных
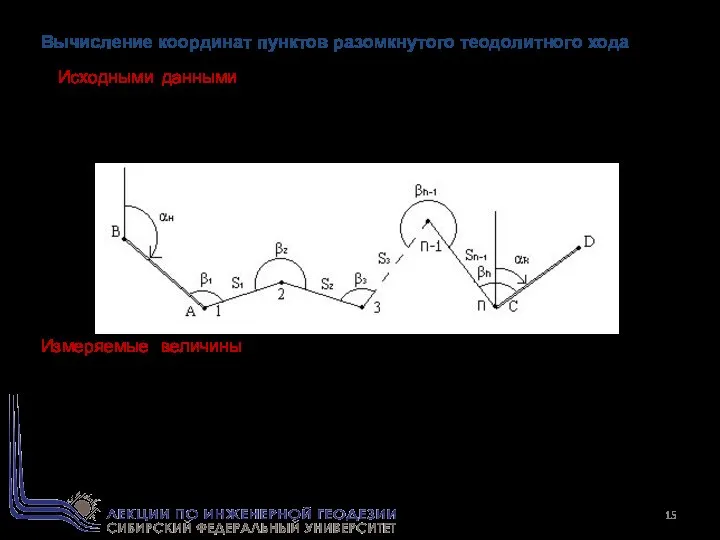
- 15. Вычисление координат пунктов разомкнутого теодолитного хода Исходными данными в теодолитном ходе являются координаты XA, YA пункта
- 16. Прямая геодезическая задача Дано: координаты точки А (ХА ;YА ), дирекционный угол направления АВ (αАВ), горизонтальная
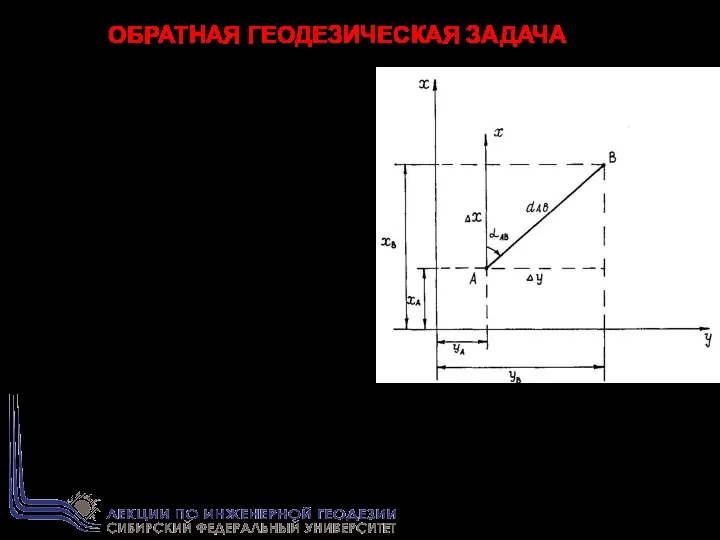
- 17. ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА Дано: Координаты точек А (ХА ;YА ), В (ХВ; YВ). Найти: дирекционный угол
- 18. ПЕРЕДАЧА ДИРЕКЦИОННОГО УГЛА НА СТОРОНУ ТЕОДОЛИТНОГО ХОДА В общем виде:
- 19. В разомкнутом теодолитном ходе должны выполняться три условия: условие дирекционных углов и два координатных условия. Вычислим
- 20. Допустимое значение угловой невязки: где n – число углов хода. Для теодолитных ходов mβ = 30",
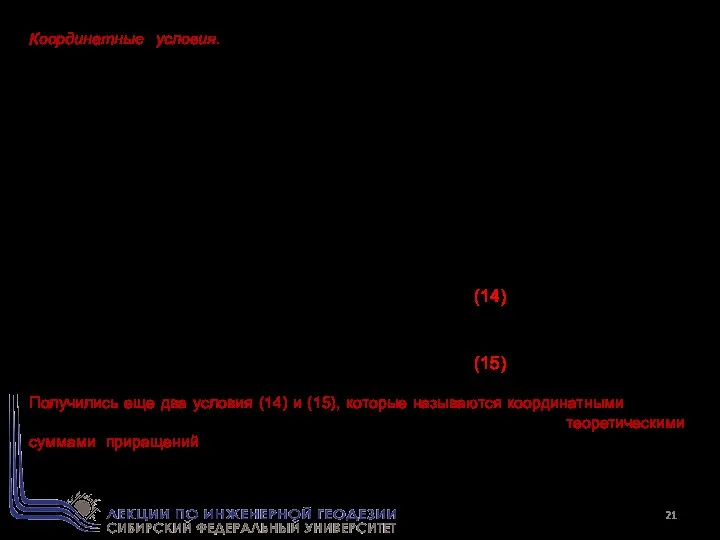
- 21. Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и
- 22. Возникают так называемые координатные невязки хода: по которым вычисляют абсолютную невязку хода: и затем относительную невязку
- 23. Вычисляют исправленные приращения координат: Зная координаты исходной точки X1 и Y1, последовательно вычисляют координаты всех вершин
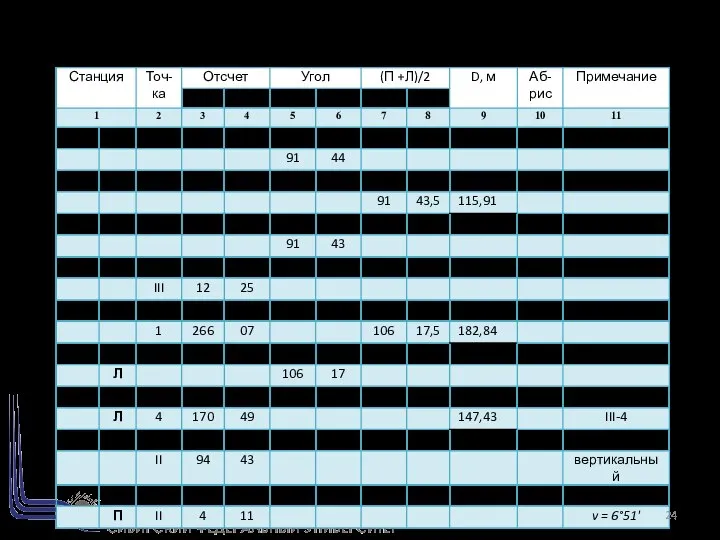
- 24. ЖУРНАЛ ИЗМЕРЕНИЙ ТЕОДОЛИТНОГО ХОДА
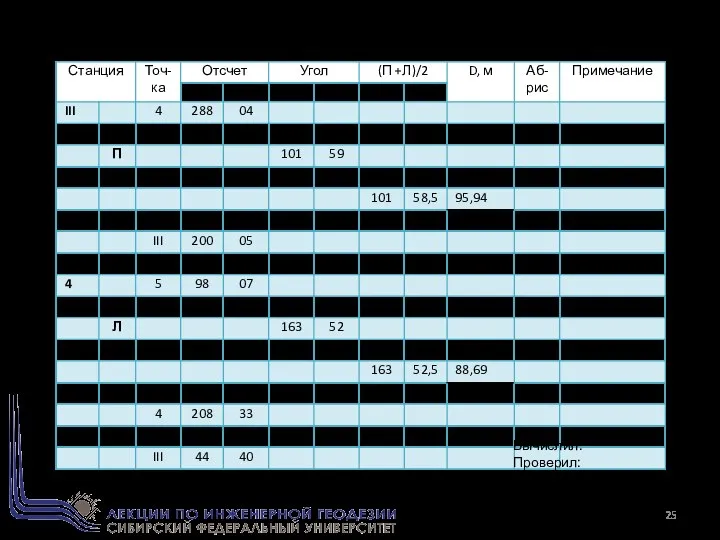
- 25. ЖУРНАЛ ИЗМЕРЕНИЙ ТЕОДОЛИТНОГО ХОДА (Продолжение) Вычислил: Проверил: Дата: ________ 200 г.
- 26. ВЕДОМОСТЬ ВЫЧИСЛЕНИЙ ТЕОДОЛИТНОГО ХОДА
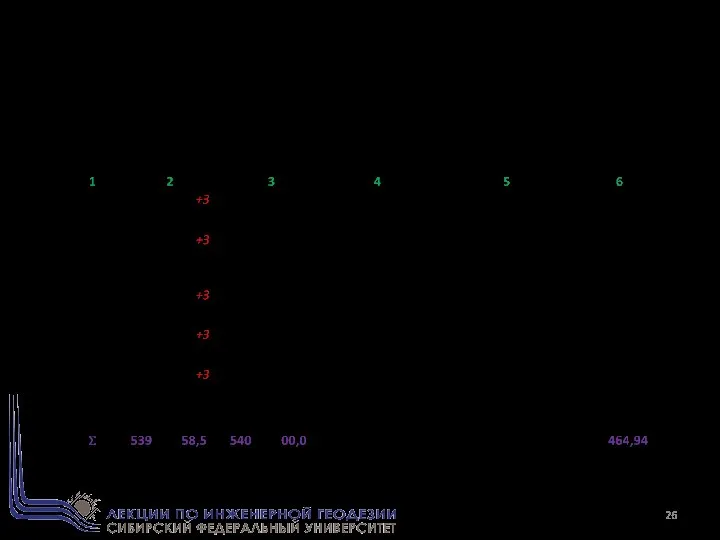
- 27. ВЕДОМОСТЬ ВЫЧИСЛЕНИЙ ТЕОДОЛИТНОГО ХОДА (Продолжение) Вычислил: Проверил: Дата: ________ 200 г.
- 28. Вычисления: Угловая невязка (замкнутый ход): Допустимая угловая невязка: где - приборная точность, n – число углов.
- 29. Поправки в измеренные углы (вводят с обратным знаком): Абсолютная невязка хода: Допустимая относительная невязка хода: что
- 31. Скачать презентацию


















 Типовые критерии отнесения товаров к группам риска и применяемые формы таможенного контроля Подготовили: Студентки 5 курса, Груп
Типовые критерии отнесения товаров к группам риска и применяемые формы таможенного контроля Подготовили: Студентки 5 курса, Груп Системы документации
Системы документации Кадровая политика организации
Кадровая политика организации Профессиональная культура учителя
Профессиональная культура учителя Гражданское общество: основные параметры и характеристики Выполнила: Рассолова Олеся группа: Т082
Гражданское общество: основные параметры и характеристики Выполнила: Рассолова Олеся группа: Т082 Европейский Союз Мировая экономика
Европейский Союз Мировая экономика МБОУ СОШ №16 г.Балаково Саратовской области.
МБОУ СОШ №16 г.Балаково Саратовской области. Критерии успешности учителя, воспитателя
Критерии успешности учителя, воспитателя Көшбасшы және көшбасшылық
Көшбасшы және көшбасшылық Поражение СОПР
Поражение СОПР HTML и CSS. CSS. (Лекция 5)
HTML и CSS. CSS. (Лекция 5) Понятие потоков ввода/вывода
Понятие потоков ввода/вывода СТО с участком диагностики двигателя
СТО с участком диагностики двигателя Как стать бухгалтером с нуля. Программа вебинара
Как стать бухгалтером с нуля. Программа вебинара Церковь Великого Устюга Спасо-Преображенская
Церковь Великого Устюга Спасо-Преображенская Чистый подход для тренеров
Чистый подход для тренеров Турфирма «Невская Ривьера». Романтические отношения в разных странах
Турфирма «Невская Ривьера». Романтические отношения в разных странах Автоматические трансмиссии
Автоматические трансмиссии Группа разработки финансовых мер по борьбе с отмыванием денег
Группа разработки финансовых мер по борьбе с отмыванием денег Господь - Пастырь мой
Господь - Пастырь мой Выпуклый анализ. Пространство подмножеств. Лекция 2
Выпуклый анализ. Пространство подмножеств. Лекция 2 Совершенствование государственной политики в сфере дорожного хозяйства Кемеровской области
Совершенствование государственной политики в сфере дорожного хозяйства Кемеровской области Язык SMS. Специфика письменного печатного общения
Язык SMS. Специфика письменного печатного общения НЕПОСЕДА – ВЕТЕРОК (учимся образовывать относительные прилагательные) Составила: учитель-логопед д/с 56 ОАО «РЖД» Власенкова
НЕПОСЕДА – ВЕТЕРОК (учимся образовывать относительные прилагательные) Составила: учитель-логопед д/с 56 ОАО «РЖД» Власенкова  5 основных стилей в одежде - от авангарда до классики
5 основных стилей в одежде - от авангарда до классики Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании "Северодвинск&quo
Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании "Северодвинск&quo Алгоритмы на тему «Графы»
Алгоритмы на тему «Графы» №1.Какие права принадлежат собственнику? 1) владение; 2) пользование; 3) распоряжение; 4) все перечисленные права;
№1.Какие права принадлежат собственнику? 1) владение; 2) пользование; 3) распоряжение; 4) все перечисленные права;