Содержание
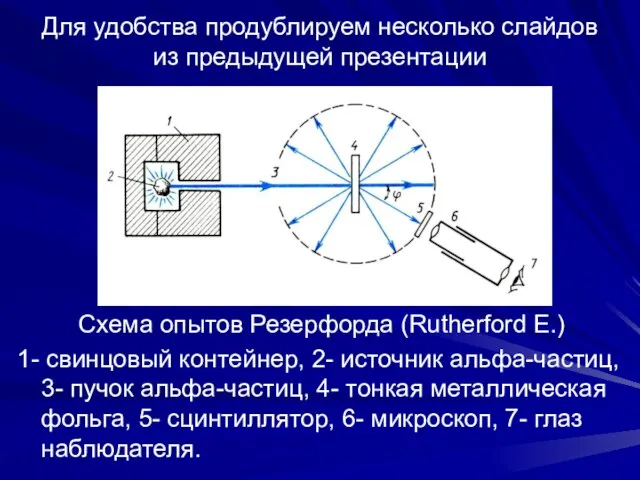
- 2. Для удобства продублируем несколько слайдов из предыдущей презентации Схема опытов Резерфорда (Rutherford E.) 1- свинцовый контейнер,
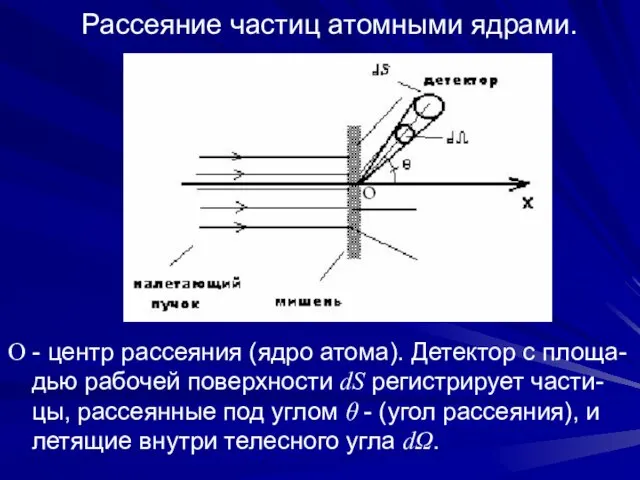
- 3. Рассеяние частиц атомными ядрами. О - центр рассеяния (ядро атома). Детектор с площа-дью рабочей поверхности dS
- 4. Количество частиц dN, летящих внутри телесного уг-ла dΩ, и зарегистрированных детектором за еди-ницу времени, равно: dN
- 5. Из формулы (2.1) находим эффективное сечение: (2.2) Разделив обе части формулы (2.2) на dΩ, находим характеристику,
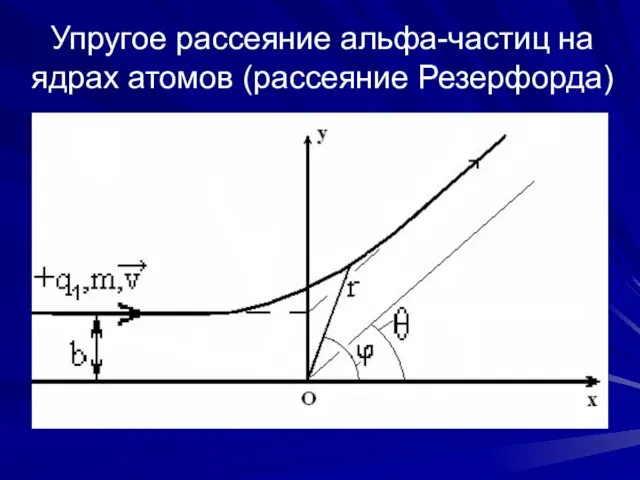
- 6. Упругое рассеяние альфа-частиц на ядрах атомов (рассеяние Резерфорда)
- 7. Для этого процесса (упругого рассеяния альфа-час-тиц на ядрах атомов) Э.Резерфорд получил фор-мулу, носящую его имя (формула
- 8. Вывод формулы Резерфорда Потенциальная энергия частицы в поле ядра: Кинетическая энергия частицы: Закон сохранения энергии имеет
- 9. Вывод формулы Резерфорда Из (2.7) находим: подставляем в (2.6): Отсюда: (2.8) Чтобы получить уравнение траектории, исключаем
- 10. Вывод формулы Резерфорда Подставляем (2.9) в (2.8): (2.10) Делаем замену переменной: и подставляем в (2.10): (2.11)
- 11. Дифференцируем (2.11) по ϕ: или (2.12) Это линейное неоднородное дифференциальное уравнение 2-го порядка. Его общее решение
- 12. Одно из частных решений уравнения (2.12) можно найти сразу: (2.14) Уравнение (2.13) - это уравнение гармонических
- 13. Чтобы найти константу В, заметим, что ордината y любой точки траектории связана с r и ϕ
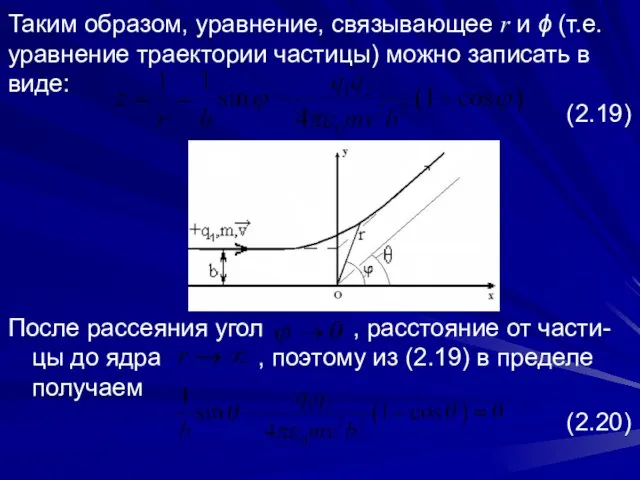
- 14. Таким образом, уравнение, связывающее r и ϕ (т.е. уравнение траектории частицы) можно записать в виде: (2.19)
- 15. Используя тригонометрические тождества запишем (2.20) в виде Отсюда получаем соотношение между углом рассея-ния θ и прицельным
- 16. Для сравнения с опытом надо вычислить эффективное сечение рассеяния Эффективное сечение равно площади кольца: (2.23) Дифференцируя
- 18. Скачать презентацию











 Electrical potentials of the cell
Electrical potentials of the cell Показатели регулирования САУ
Показатели регулирования САУ Анодные процессы при коррозии металлов
Анодные процессы при коррозии металлов Системы тормозов
Системы тормозов Развитие ракетной техники
Развитие ракетной техники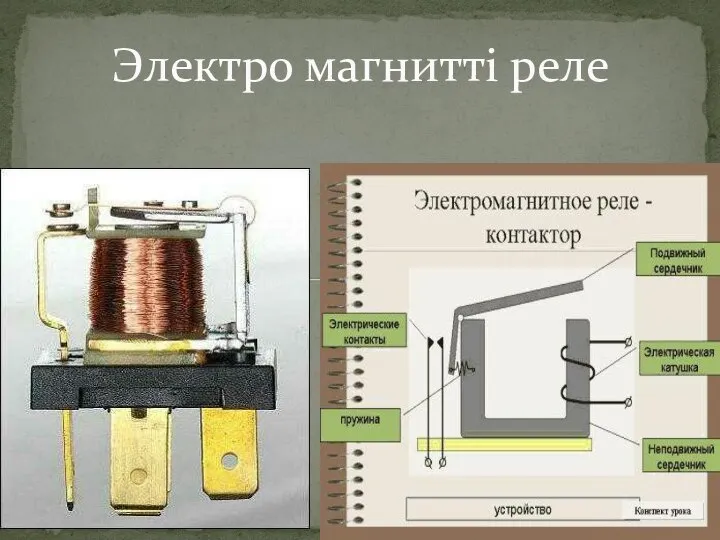 Электро магнитті реле
Электро магнитті реле Сила трения. Трение покоя. Взаимодействие тел. Урок 28/22 7 класс Учитель: Ермакова Мира Владимировна МОУ «ООШ х.Малая Скатовка Сар
Сила трения. Трение покоя. Взаимодействие тел. Урок 28/22 7 класс Учитель: Ермакова Мира Владимировна МОУ «ООШ х.Малая Скатовка Сар Лазерная обработка
Лазерная обработка Model de elaborare a raportului
Model de elaborare a raportului Презентация по физике "Электрический ток" - скачать
Презентация по физике "Электрический ток" - скачать  Пневматический тормозной привод
Пневматический тормозной привод Электро-магнитные волны. Лекция 7
Электро-магнитные волны. Лекция 7 Теория динамических систем. Введение
Теория динамических систем. Введение Презентация по физике "Механические колебания и волны. Акустика" - скачать
Презентация по физике "Механические колебания и волны. Акустика" - скачать  Виды технического обслуживания
Виды технического обслуживания Насосы
Насосы Архімед
Архімед Хаос и катастрофы
Хаос и катастрофы Сучасні економічні джерела світла
Сучасні економічні джерела світла  Термодинамические законы
Термодинамические законы Қатты диэлектриктің жылулық және ионизациялық тесілуі
Қатты диэлектриктің жылулық және ионизациялық тесілуі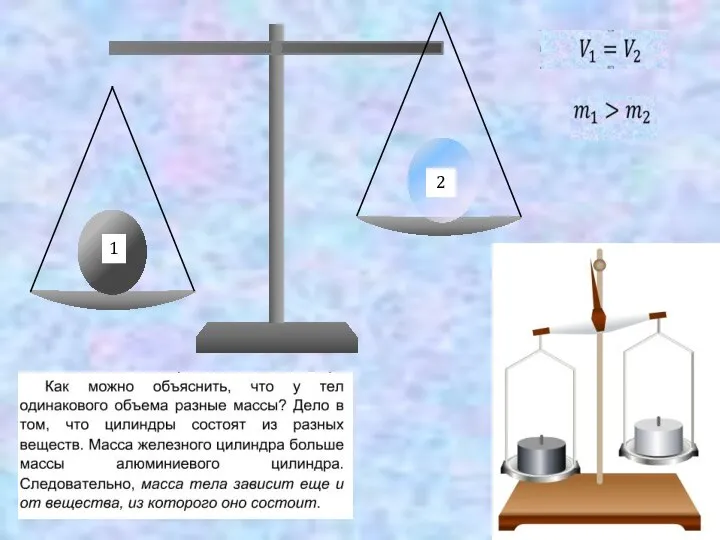 Плотность вещества
Плотность вещества Общая физика. Механика
Общая физика. Механика Аттестационная работа. Решение исследовательских задач по физике, как способ формирования исследовательских компетенций учащихс
Аттестационная работа. Решение исследовательских задач по физике, как способ формирования исследовательских компетенций учащихс Проверочный расчет двигателя 6 L21\31
Проверочный расчет двигателя 6 L21\31 Малоразмерный газотурбинный двигатель мощностью 150 кВт
Малоразмерный газотурбинный двигатель мощностью 150 кВт Презентация по физике "Измерение объема твердого тела" - скачать
Презентация по физике "Измерение объема твердого тела" - скачать  Программа диагностики автомобиля, уровень пассажира (SDP, PL-1). Основы технологии шасси
Программа диагностики автомобиля, уровень пассажира (SDP, PL-1). Основы технологии шасси