Содержание
- 2. Формулировки и формула Сформулируйте и запишите с помощью букв a, b и c теорему Пифагора. Сформулируйте
- 3. Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Применяется при нахождении неизвестной стороны
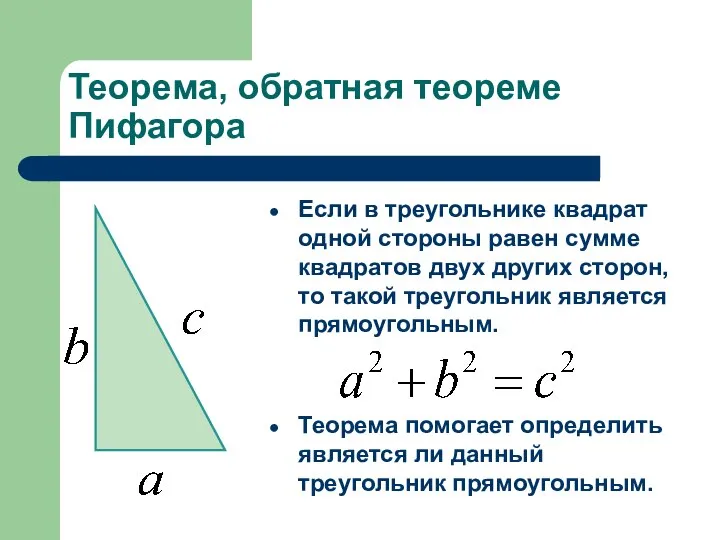
- 4. Теорема, обратная теореме Пифагора Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон,
- 5. Задача №1 В прямоугольном треугольнике катеты равны 6 см и 8 см. Чему равна гипотенуза?
- 6. Задача №2 В прямоугольном треугольнике гипотенуза равна 13 см, а один из катетов – 12 см.
- 7. Задача №3 Определите, является ли прямоугольным треугольник со сторонами 8 м, 5 м и 9 м.
- 8. Задача №4 В треугольнике две стороны равны соответственно 20 см и 15 см. Какой должна быть
- 9. Задача №5 Диагонали ромба равны 16 см и 12 см. Вычислите: а) сторону ромба; б) расстояние
- 10. Задача №6 В прямоугольной трапеции большая боковая сторона и меньшая диагональ равны по 13 см, а
- 12. Скачать презентацию








 Теорема Пифагора и способы ее доказательства - презентация по Геометрии
Теорема Пифагора и способы ее доказательства - презентация по Геометрии Зарождение геометрии Геометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, прок
Зарождение геометрии Геометрия возникла в результате практической деятельности людей: нужно было сооружать жилища, храмы, прок Медианы треугольника Свойства медиан
Медианы треугольника Свойства медиан Объем прямой призмы
Объем прямой призмы «Число, положение и комбинаторика – три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все математичес
«Число, положение и комбинаторика – три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все математичес Урок математики в 4-м классе по теме "Виды треугольников" Выполнила: Лихачёва Любовь Николаевна  
Урок математики в 4-м классе по теме "Виды треугольников" Выполнила: Лихачёва Любовь Николаевна   ГБОУ СОШ №593 с углубленным изучением английского языка Невского района Санкт-Петербурга Презентация по математике на тему:
ГБОУ СОШ №593 с углубленным изучением английского языка Невского района Санкт-Петербурга Презентация по математике на тему:  История симметрии
История симметрии Доклад на тему: «Вневписанная окружность» Номинация: математика Выполнили: Коляда Валентина Афонина Екатерина ученицы 9м класс
Доклад на тему: «Вневписанная окружность» Номинация: математика Выполнили: Коляда Валентина Афонина Екатерина ученицы 9м класс Начальные геометрические сведения Учитель математики МКОУ « Москаленский лицей» Бадюк Ольга Ярославна
Начальные геометрические сведения Учитель математики МКОУ « Москаленский лицей» Бадюк Ольга Ярославна  Признаки параллельности двух прямых - презентация по Геометрии
Признаки параллельности двух прямых - презентация по Геометрии Работу выполнили:Шабалина Мария и Ганджалян Жанна Преподаватель геометрии: Хайбрахманова Г.Ф.
Работу выполнили:Шабалина Мария и Ганджалян Жанна Преподаватель геометрии: Хайбрахманова Г.Ф. Урок №21 Построение сечений параллелепипеда
Урок №21 Построение сечений параллелепипеда  Проецирование предметов на две и три взаимно перпендикулярные плоскости проекций - презентация по Геометрии
Проецирование предметов на две и три взаимно перпендикулярные плоскости проекций - презентация по Геометрии Второй признак подобия треугольников
Второй признак подобия треугольников 11. 09. 13 Многоугольник. Выпуклый многоугольник. Четырехугольник.
11. 09. 13 Многоугольник. Выпуклый многоугольник. Четырехугольник.  ЭЛЕМЕНТЫ ТРИГОНОМЕТРИИ РАДИАННАЯ МЕРА УГЛА МОУ Василёвская СОШ Починковского р-на Нижегородской обл. Учитель: Архипкина И.В.
ЭЛЕМЕНТЫ ТРИГОНОМЕТРИИ РАДИАННАЯ МЕРА УГЛА МОУ Василёвская СОШ Починковского р-на Нижегородской обл. Учитель: Архипкина И.В. .Действия с векторами
.Действия с векторами  Применение подобия к доказательству теорем и решению задач
Применение подобия к доказательству теорем и решению задач Признаки равенства треугольников - презентация по Геометрии
Признаки равенства треугольников - презентация по Геометрии Такая известная теорема Пифагора - презентация по Геометрии_
Такая известная теорема Пифагора - презентация по Геометрии_ Занимательная математика Алгебра и начала математического анализа, 10 класс.
Занимательная математика Алгебра и начала математического анализа, 10 класс.  Длина окружности и площадь круга. Решение задач.
Длина окружности и площадь круга. Решение задач.  Проект «Математика в профессии «Повар, кондитер» Автор: преподаватель ГОУ СПО ПК № 33 Симоненко Е.Е.
Проект «Математика в профессии «Повар, кондитер» Автор: преподаватель ГОУ СПО ПК № 33 Симоненко Е.Е. Тема проекта Построение общих касательных к двум окружностям на плоскости.
Тема проекта Построение общих касательных к двум окружностям на плоскости.  Урок 2 9 класс
Урок 2 9 класс Выполнила Иванова Галина Ивановна преподаватель математики Кадетского Корпуса Лицея № 38
Выполнила Иванова Галина Ивановна преподаватель математики Кадетского Корпуса Лицея № 38 Справочное пособие по геометрии – 7 класс Школьникам Учителям Родителям
Справочное пособие по геометрии – 7 класс Школьникам Учителям Родителям