Содержание
- 2. Цели урока: Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на
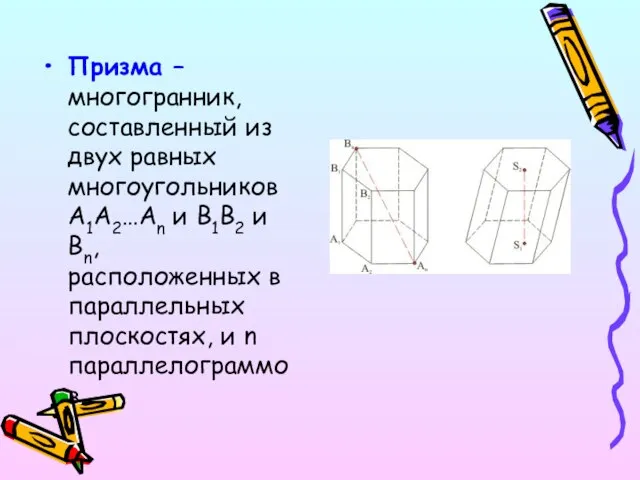
- 3. Призма – многогранник, составленный из двух равных многоугольников A1A2…An и B1B2 и Bn, расположенных в параллельных
- 4. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. Прямая призма называется правильной, если
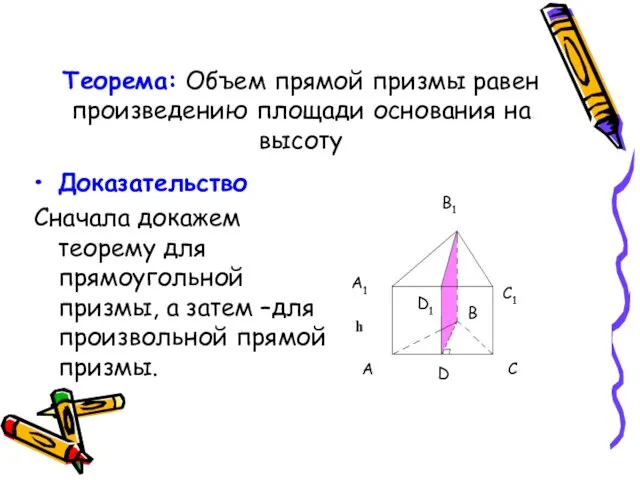
- 5. Теорема: Объем прямой призмы равен произведению площади основания на высоту Доказательство Сначала докажем теорему для прямоугольной
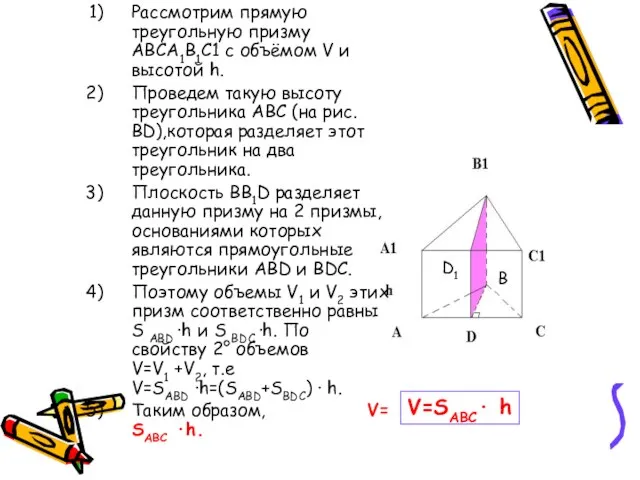
- 6. Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V и высотой h. Проведем такую высоту треугольника ABC
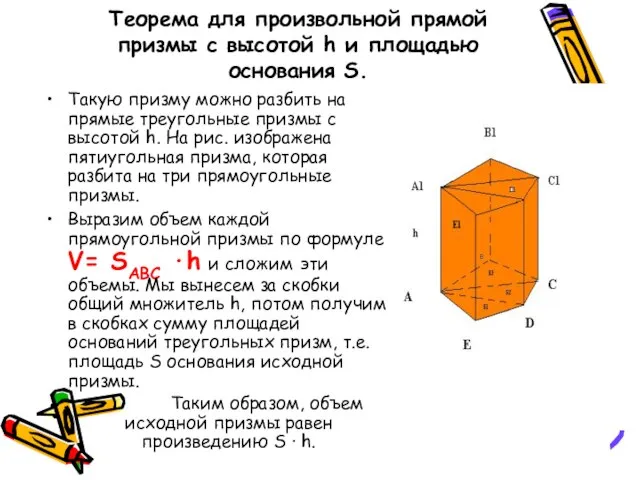
- 7. Теорема для произвольной прямой призмы с высотой h и площадью основания S. Такую призму можно разбить
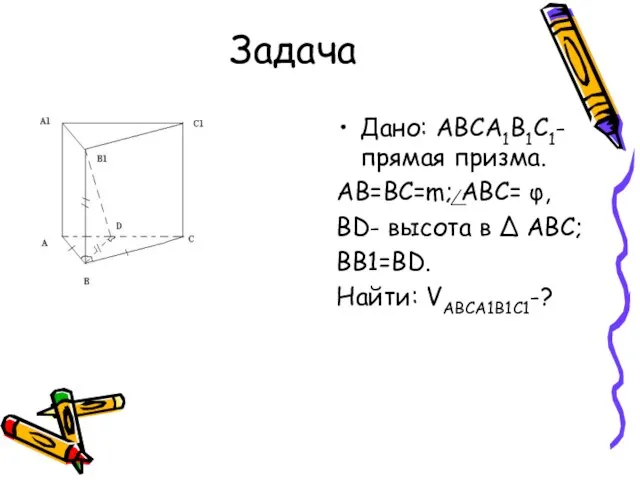
- 8. Задача Дано: ABCA1B1C1- прямая призма. AB=BC=m; ABC= φ, BD- высота в ∆ ABC; BB1=BD. Найти: VABCA1B1C1-?
- 9. Решение: S ABC ·h, h=BB1. Рассмотрим ∆ ABC; ∆ ABC- р/б. BD- высота ∆ ABC, следовательно
- 10. Вопросы: Как найти объем прямой призмы? Основные шаги при доказательстве теоремы прямой призмы?
- 11. Работу выполнили: Шахбазян Эллена,11”В” Шмырева Юлия,11 “В” Двадненко Аня,11 “В”
- 13. Скачать презентацию





 Движение геометрия 9 класс - презентация по Геометрии
Движение геометрия 9 класс - презентация по Геометрии Презентация на тему: «Параллелепипед» Выполнила :ученица 10А класса МБОУСОШ№27 Павлова Ольга. Учитель : Ветрова Людмила Ивано
Презентация на тему: «Параллелепипед» Выполнила :ученица 10А класса МБОУСОШ№27 Павлова Ольга. Учитель : Ветрова Людмила Ивано Тема урока: «Геометрические задачи на экзаменах»
Тема урока: «Геометрические задачи на экзаменах»  Задачи на готовых чертежах - презентация по Геометрии
Задачи на готовых чертежах - презентация по Геометрии Первый признак подобия треугольников
Первый признак подобия треугольников Презентация по геометрии Равнобедренный треугольник
Презентация по геометрии Равнобедренный треугольник  Зачем нужна геометрия? Кобыльская Олеся Михайлова Алеся Бирюкова Тоня Зубарева Настя Харитонова Полина Кузуб Оля
Зачем нужна геометрия? Кобыльская Олеся Михайлова Алеся Бирюкова Тоня Зубарева Настя Харитонова Полина Кузуб Оля  Урок геометрии в 10-м классе по теме: "Введение декартовых координат в пространстве. Расстояние между точками. Координаты сер
Урок геометрии в 10-м классе по теме: "Введение декартовых координат в пространстве. Расстояние между точками. Координаты сер Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Координатная плоскость - презентация по Геометрии
Координатная плоскость - презентация по Геометрии Геометрические тела. Многогранники. Для учащихся 5 классов
Геометрические тела. Многогранники. Для учащихся 5 классов Такая разная геометрия - презентация по Геометрии
Такая разная геометрия - презентация по Геометрии Виды правильных многогранников - презентация по Геометрии
Виды правильных многогранников - презентация по Геометрии Подготовка к ГИА по геометрии Треугольники
Подготовка к ГИА по геометрии Треугольники Открытый урок по геометрии в 9 классе. Тема: «Формулы для вычисления площади треугольника» Учитель математики МОУ СОШ № 4 и
Открытый урок по геометрии в 9 классе. Тема: «Формулы для вычисления площади треугольника» Учитель математики МОУ СОШ № 4 и Подобные треугольники Учитель школы №20 Смотрина Валентина Петровна
Подобные треугольники Учитель школы №20 Смотрина Валентина Петровна Прямые. Скрещивающиеся - презентация по Геометрии_
Прямые. Скрещивающиеся - презентация по Геометрии_ СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА Динамические модели геометрических фигур - презентация по Геометрии
Динамические модели геометрических фигур - презентация по Геометрии Вдохновение нужно в геометрии не меньше, чем в поэзии. А.С.Пушкин
Вдохновение нужно в геометрии не меньше, чем в поэзии. А.С.Пушкин  Потенциал исследовательской деятельности в осуществлении профильного обучения Подготовлено Г.И. Винокуровой г. Елец, МОУ Ли
Потенциал исследовательской деятельности в осуществлении профильного обучения Подготовлено Г.И. Винокуровой г. Елец, МОУ Ли ГРМ
ГРМ  Геометрия МОУ Серковская СОШ Цитович Алексей Федорова Ирина Юрьевна
Геометрия МОУ Серковская СОШ Цитович Алексей Федорова Ирина Юрьевна «Орнамент - математическое воплощение красоты» Учитель математики МОУ Хотьковская средняя общеобразовательная школа №5 Сидоро
«Орнамент - математическое воплощение красоты» Учитель математики МОУ Хотьковская средняя общеобразовательная школа №5 Сидоро Второй признак равенства треугольников Цели урока: 1)доказать второй признак равенства треугольников, 1)выработать у учащихся на
Второй признак равенства треугольников Цели урока: 1)доказать второй признак равенства треугольников, 1)выработать у учащихся на Введение в стереометрию - презентация по Геометрии
Введение в стереометрию - презентация по Геометрии Длина окружности - презентация по Геометрии
Длина окружности - презентация по Геометрии