Содержание
- 2. Основанием треугольной призмы является равнобедренный прямоугольный треугольник. Ровно одна ее грань — квадрат, известны длины ее
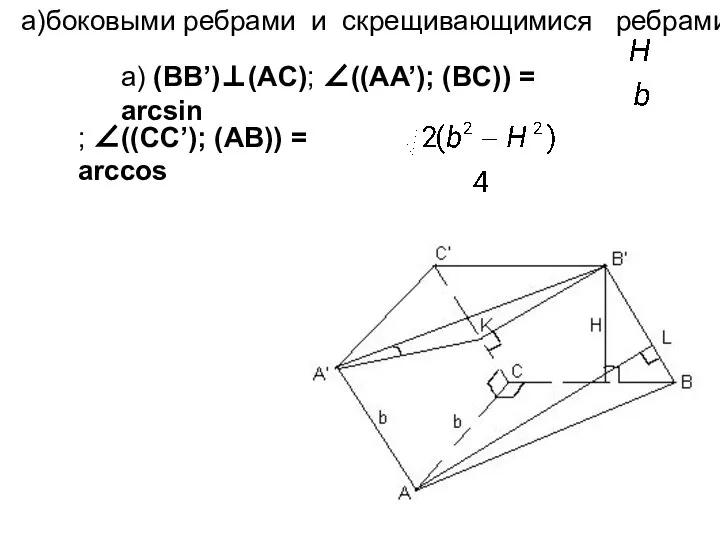
- 3. а) (BB’)⊥(AC); ∠((AA’); (BC)) = arcsin ; ∠((CC’); (AB)) = arccos а)боковыми ребрами и скрещивающимися ребрами
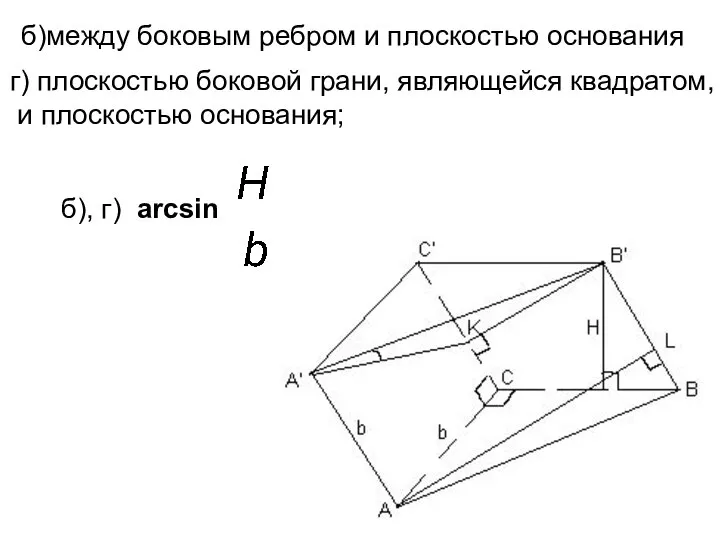
- 4. б), г) arcsin б)между боковым ребром и плоскостью основания г) плоскостью боковой грани, являющейся квадратом, и
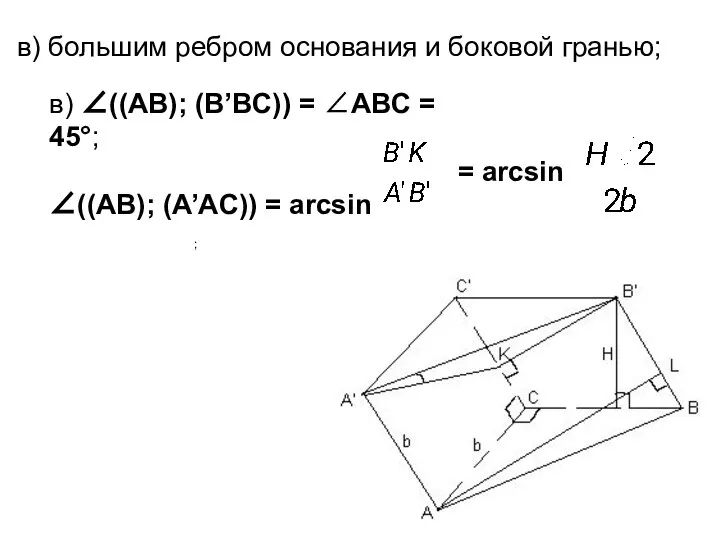
- 5. ; в) ∠((AB); (B’BC)) = ∠ABC = 45°; ∠((AB); (A’AC)) = arcsin в) большим ребром основания
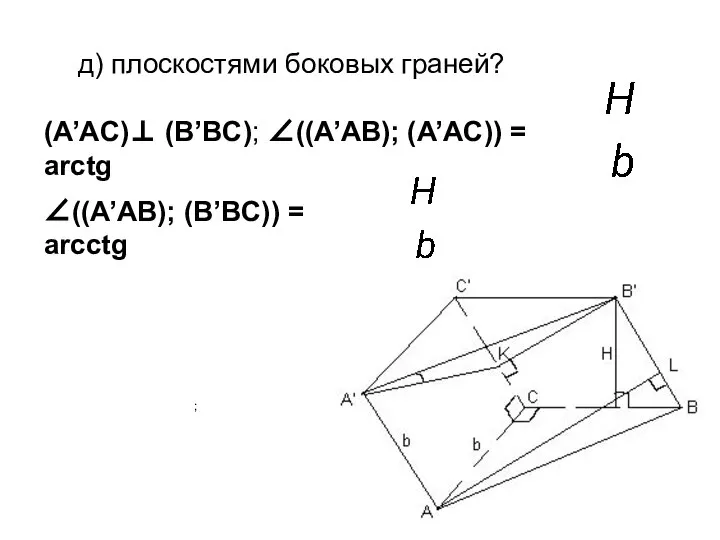
- 6. д) плоскостями боковых граней? ; (A’AC)⊥ (B’BC); ∠((A’AB); (A’AC)) = arctg ∠((A’AB); (B’BC)) = arcctg
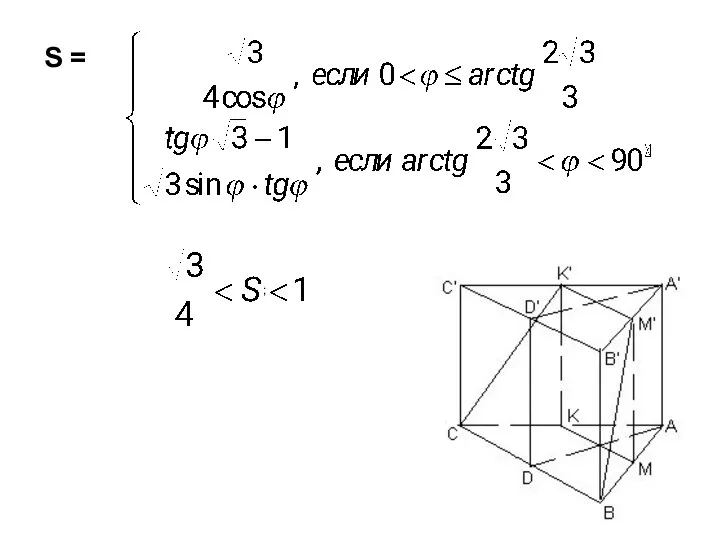
- 7. ; S =
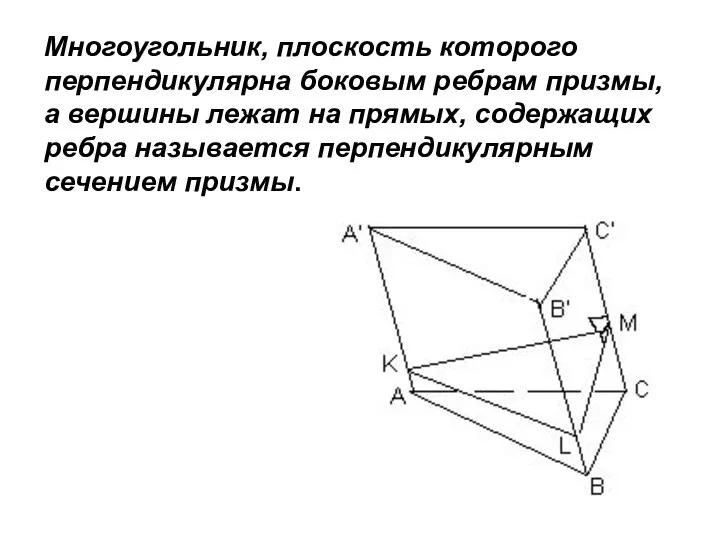
- 8. Многоугольник, плоскость которого перпендикулярна боковым ребрам призмы, а вершины лежат на прямых, содержащих ребра называется перпендикулярным
- 9. Как построить перпендикулярное сечение призмы? Является ли оно сечением призмы? Сколько перпендикулярных сечений у любой призмы?
- 10. Докажите, что точки касания вписанного в призму шара с ее боковыми гранями лежат в одном из
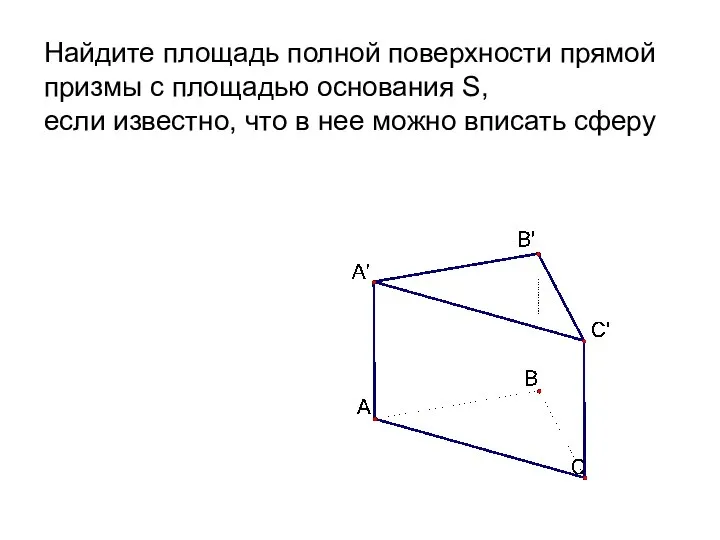
- 11. Найдите площадь полной поверхности прямой призмы с площадью основания S, если известно, что в нее можно
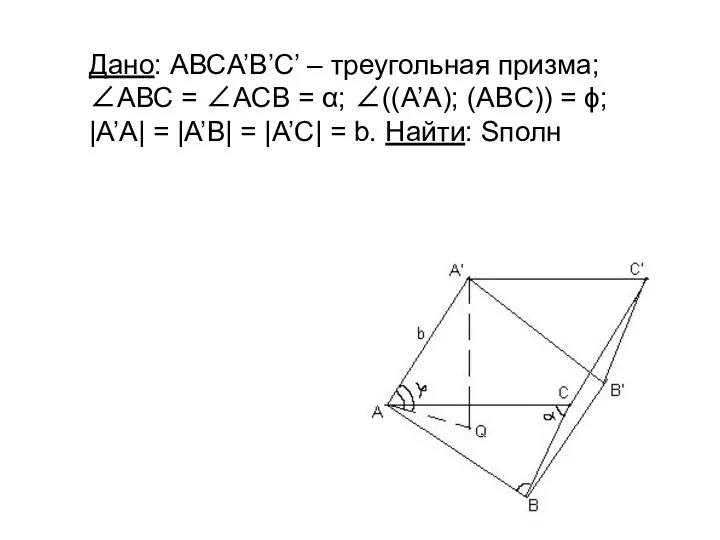
- 12. Дано: АВСA’B’C’ – треугольная призма; ∠АВС = ∠АСB = α; ∠((A’A); (ABC)) = ϕ; |A’A| =
- 13. Уроки 6 Параллелепипед
- 14. Сколько граней, являющихся прямоугольниками, может быть в параллелепипеде?
- 15. Установите вид параллелепипеда, если: а) все его грани равны; б) все его грани равновелики; в) все
- 16. Докажите, что результат пункта ж) около него можно описать сферу является Н. и Д. условием описания
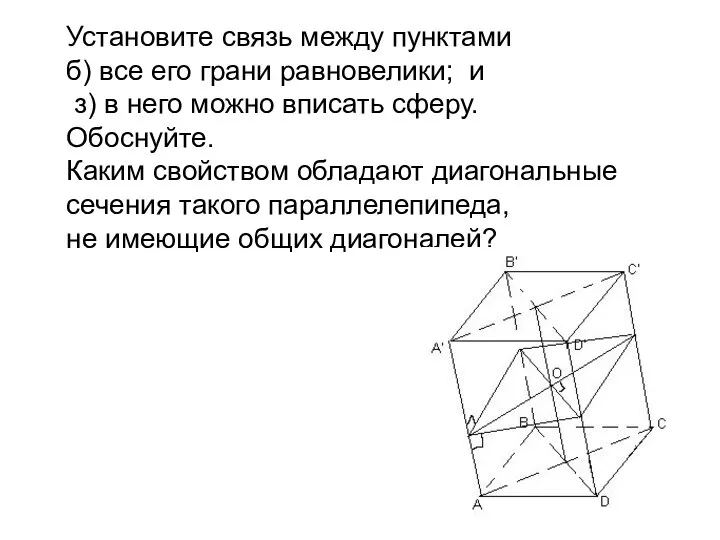
- 17. Установите связь между пунктами б) все его грани равновелики; и з) в него можно вписать сферу.
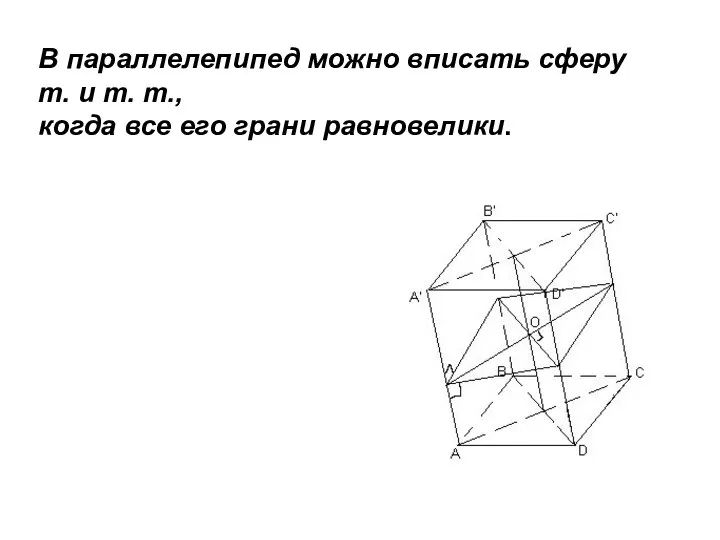
- 18. В параллелепипед можно вписать сферу т. и т. т., когда все его грани равновелики.
- 19. Все грани параллелепипеда АВСDA1В1С1D1 — ромбы. Их равные острые углы сходятся в вершине А. Пусть каждое
- 20. Все грани параллелепипеда АВСDA1В1С1D1 — ромбы. Их равные острые углы сходятся в вершине А. Пусть каждое
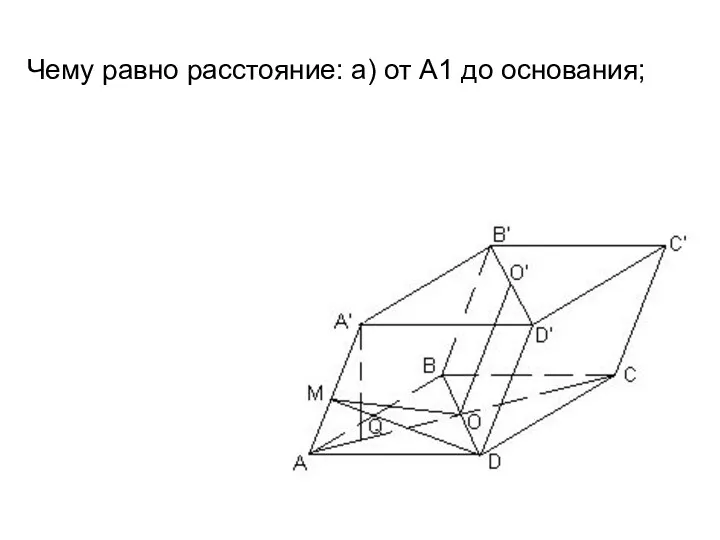
- 21. Чему равно расстояние: а) от A1 до основания;
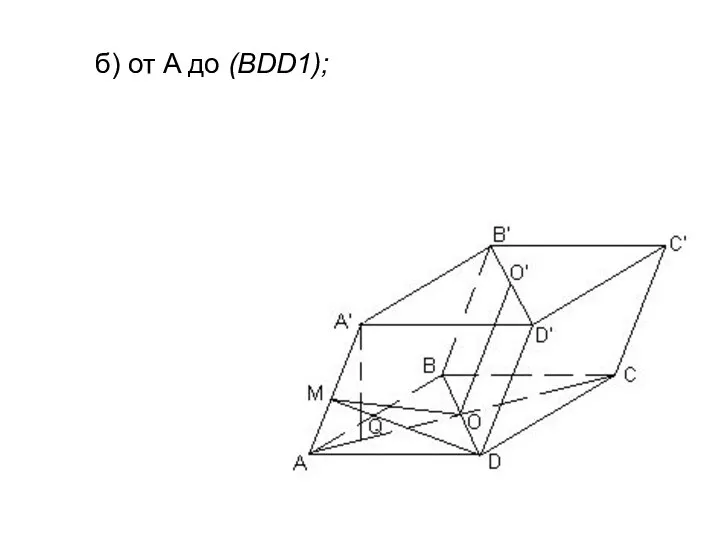
- 22. б) от A до (BDD1);
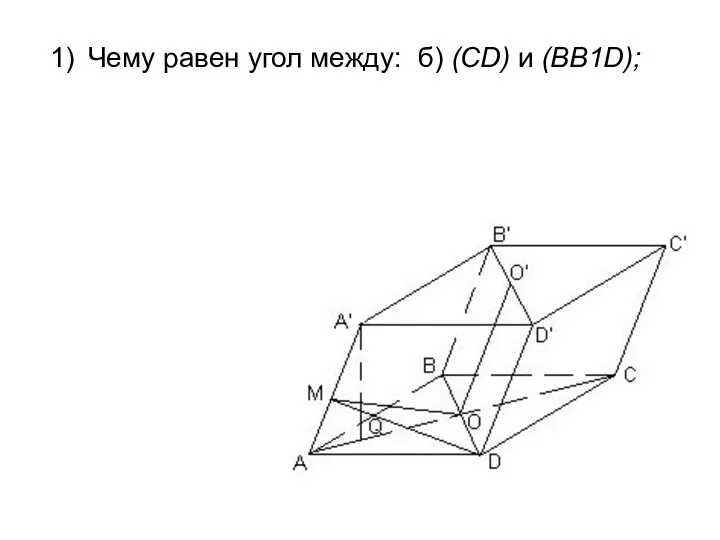
- 23. Чему равен угол между: б) (CD) и (BB1D);
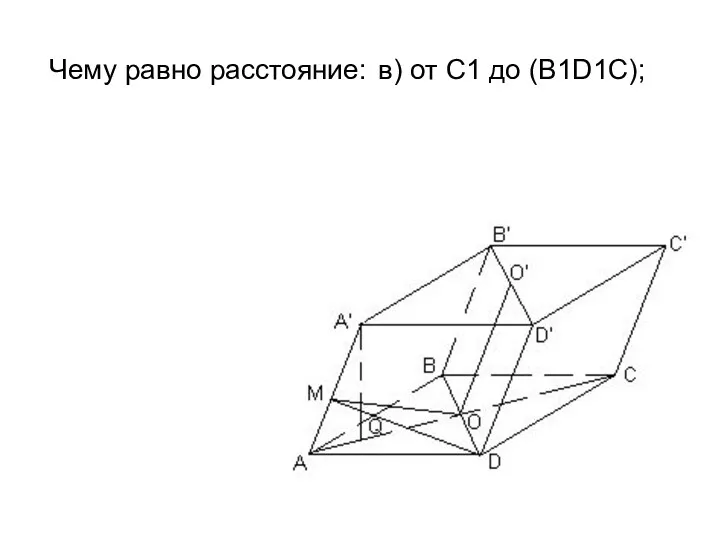
- 24. Чему равно расстояние: в) от С1 до (В1D1С);
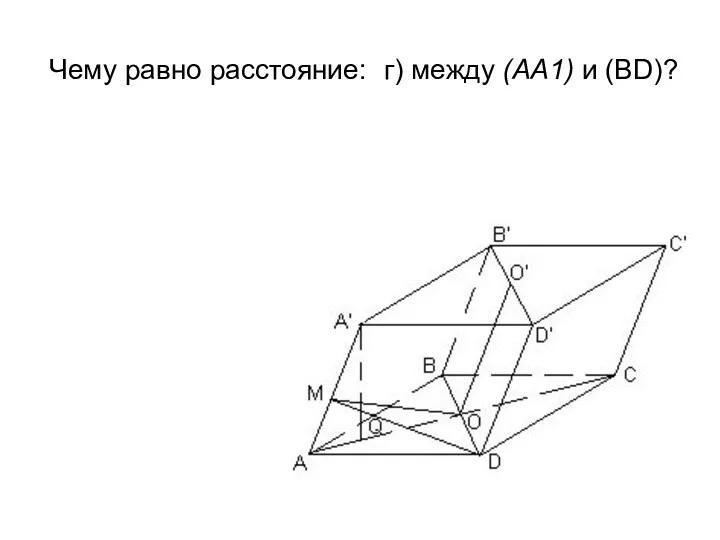
- 25. Чему равно расстояние: г) между (AA1) и (BD)?
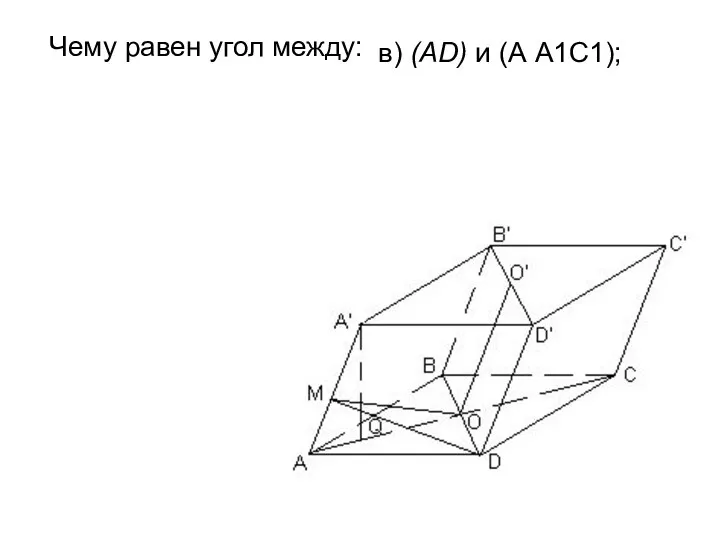
- 26. Чему равен угол между: в) (AD) и (А А1С1);
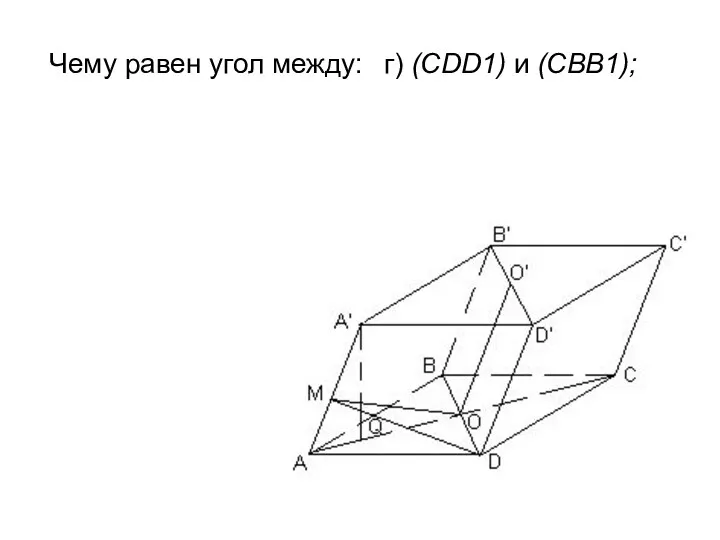
- 27. Чему равен угол между: г) (CDD1) и (CBB1);
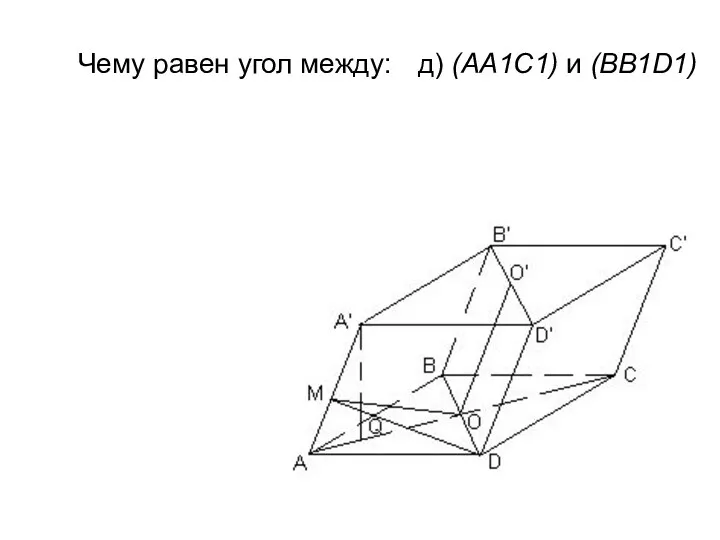
- 28. Чему равен угол между: д) (АА1С1) и (BB1D1)
- 30. Скачать презентацию









 Теорема о трех перпендикулярах
Теорема о трех перпендикулярах  Правильные многоугольники (9 класс) - презентация по Геометрии_
Правильные многоугольники (9 класс) - презентация по Геометрии_ Геометрия 7 класс. МОУ «Гимназия №22 города Белгорода» Работу выполнили учащиеся: Козяр Д.(7 «В»),Загребайлов Д.(7 «В»), Боброва К.(
Геометрия 7 класс. МОУ «Гимназия №22 города Белгорода» Работу выполнили учащиеся: Козяр Д.(7 «В»),Загребайлов Д.(7 «В»), Боброва К.( Геометрия и мода Составила Федосеева учитель математики ДСОШ № 2
Геометрия и мода Составила Федосеева учитель математики ДСОШ № 2  Построения в пространстве. геометрия 10
Построения в пространстве. геометрия 10 Золотое сечение - презентация по Геометрии
Золотое сечение - презентация по Геометрии Тема «Особенности построения на клетчатой бумаге»
Тема «Особенности построения на клетчатой бумаге» Появление неравенства и знати - урок истории Древнего мира - презентация по Геометрии
Появление неравенства и знати - урок истории Древнего мира - презентация по Геометрии Решение задач на применение признаков подобия треугольников - презентация по Геометрии
Решение задач на применение признаков подобия треугольников - презентация по Геометрии Решение треугольников.
Решение треугольников. Презентация учителя по историческим сведениям и введению нового материала. Тема «Площади четырехугольников». 8 класс.
Презентация учителя по историческим сведениям и введению нового материала. Тема «Площади четырехугольников». 8 класс.  Геометрия 10 «А» класс 18.03.2008
Геометрия 10 «А» класс 18.03.2008 Сумма двух векторов. Геометрия 9 класс
Сумма двух векторов. Геометрия 9 класс ОСЕВАЯ И ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
ОСЕВАЯ И ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Прямоугольный труегольник - презентация по Геометрии
Прямоугольный труегольник - презентация по Геометрии Проблема четырех красок
Проблема четырех красок Соотношения между сторонами и углами в прямоугольном треугольнике - презентация по Геометрии____________________________________________________________________
Соотношения между сторонами и углами в прямоугольном треугольнике - презентация по Геометрии____________________________________________________________________ Презентация по геометрии Многоугольник. Выпуклый многоугольник. Четырехугольник.
Презентация по геометрии Многоугольник. Выпуклый многоугольник. Четырехугольник.  Презентация на тему "Теорема косинусов"
Презентация на тему "Теорема косинусов" Равнобедренный треугольник
Равнобедренный треугольник Пирамида Хеопса – немой трактат по геометрии. Что означает владение математикой? Это есть умение решать задачи, причём не толь
Пирамида Хеопса – немой трактат по геометрии. Что означает владение математикой? Это есть умение решать задачи, причём не толь Решение прямоугольных треугольников - презентация по Геометрии
Решение прямоугольных треугольников - презентация по Геометрии Тема урока: «Правильная пирамида».
Тема урока: «Правильная пирамида». Пирамиды Подготовили ученицы 5 класса «А» Власова Анастасия и Шустикова Анастасия
Пирамиды Подготовили ученицы 5 класса «А» Власова Анастасия и Шустикова Анастасия ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Наглядное пособие для уроков черчения Учитель: Бурякова И.М.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Наглядное пособие для уроков черчения Учитель: Бурякова И.М. «Магическая фигура - треугольник»
«Магическая фигура - треугольник»  ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ВОКРУГ НАС Автор Трухина Галина. Руководитель Канина Галина Владимировна
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ВОКРУГ НАС Автор Трухина Галина. Руководитель Канина Галина Владимировна Тест, для проверки знаний по геометрии за 7-8кл. Подготовила: Миронова Анастасия, 8А, шк.1.
Тест, для проверки знаний по геометрии за 7-8кл. Подготовила: Миронова Анастасия, 8А, шк.1.